Вычисление площадей фигур с помощью определенного интеграла

1. Правило вычисления площадей плоских фигур
Определенный интеграл от непрерывной неотрицательной функции равен площади соответствующей криволинейной трапеции:
Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:
1. По условию задачи сделать схематический чертеж.
2.Представить искомую площадь как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определить пределы интегрирования для каждой составляющей криволинейной трапеций.
3.Записать каждую функцию в виде
4.Вычислить площади каждой криволинейной трапеции и площадь искомой фигуры.

2.Площади фигур, расположенных над осью Оx
Пусть на тотрезке [a,b] функция f(x) принимает неотрицательные значения,т.е для любого .Тогда график функции расположен над осью Ох.Если фигура,расположенная над осью Ох, являются криволинейной трапецией,то ее площадь вычисляется по известной формуле:
Н-р:Вычислить площадь фигуры, ограниченной заданными линиями:
Р-е:
16 25

3.Площади фигур, расположенных полностью или частично под осью Ох
Пусть на отрезке [a,b] задана неположительная непрерывная функция ,т.е. для любого . Тогдм график функции расположен под осью Ох.
Если фигура, расположенная над осью Ох, является криволинейной трапецией, то её площадь вычисляется по формуле
Н-р:
Y=-2x
0
X=3
Р-е:

4.Площади фигур, прилегающих к оси Оу
Если криволинейная трапеция прилегает к оси ординат и ограничена непрерывной кривой ,прямыми y=a,y=b и осью Оу,то её площадь вычисляется по формуле:
Н-р:
Р-е:
9
4
3
0

5.Симметрично расположенные плоские фигуры
Если кривая расположена симметрично относительно оси координат или начала координат, то можно упростить вычисления, определив половину площади и затем удвоив результат.
Н-р:
Р-е:
2
-2
5

Решение примеров
№1
№2
№3
№4 Вычислить площадь, ограниченной кривыми

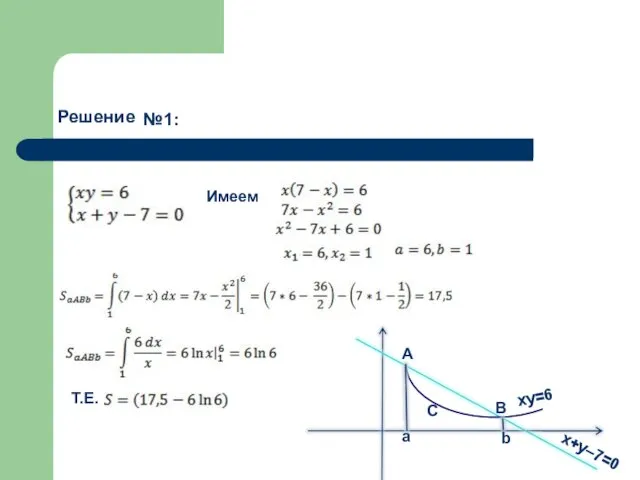
№1:
Решение
Имеем
Т.Е.
ху=6
В
b
C
А
а
x+y–7=0

Решение №2
пересекает ось абцисс в точках
Парабола
площади частей этой фигуры,соответствующих отрезкам [0,4] и [4,5]
- искомая площадь,тогда
С-но:
5
4
х=5

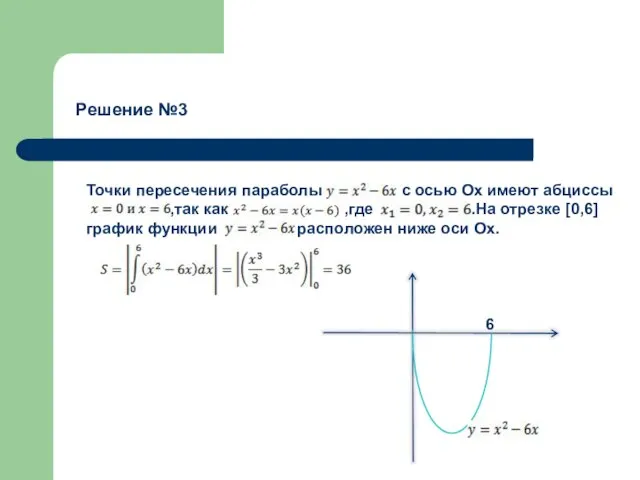
Решение №3
Точки пересечения параболы с осью Ох имеют абциссы
,так как ,где .На отрезке [0,6]
график функции расположен ниже оси Ох.
6