Содержание
- 2. "Мастерство - это то, чего можно добиться" А.С. Макаренко
- 3. Цели урока: Показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя
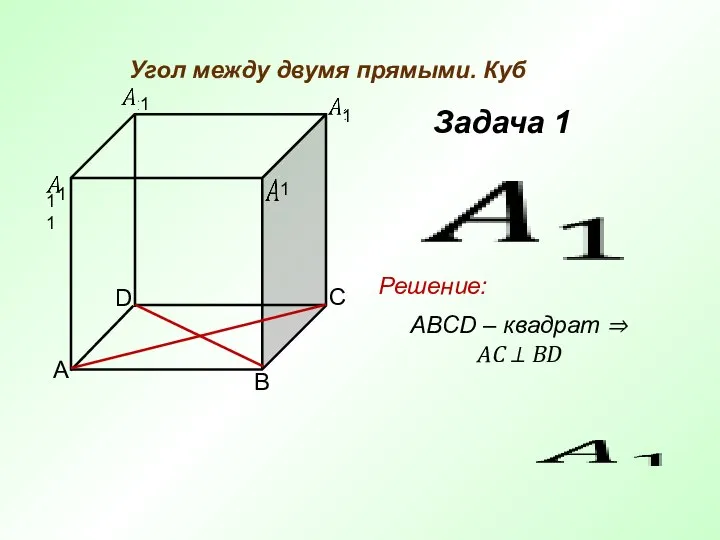
- 4. 11 Задача 1 Угол между двумя прямыми. Куб ABCD – квадрат ⇒ AC ⊥ BD Решение:
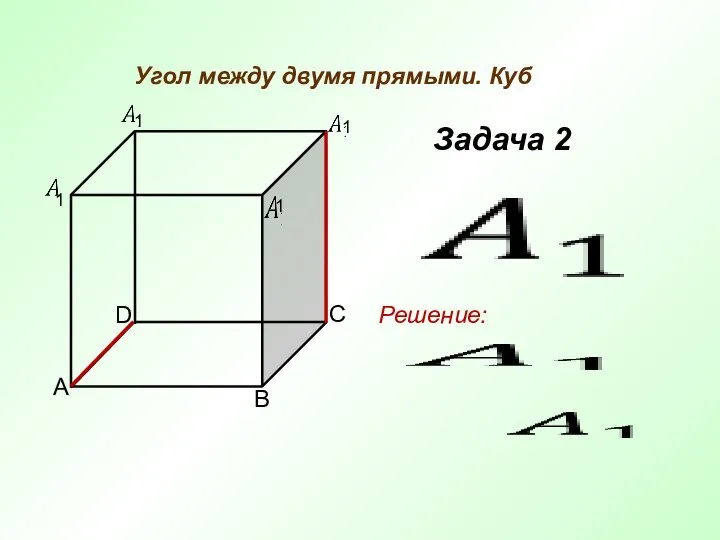
- 5. Угол между двумя прямыми. Куб Задача 2 A C B D Решение: 1 1 1 1
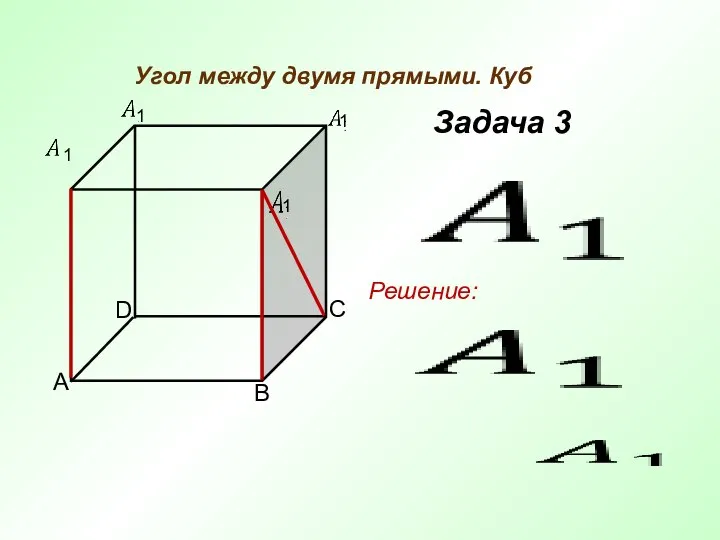
- 6. Угол между двумя прямыми. Куб Задача 3 Решение: 1 1 1 1
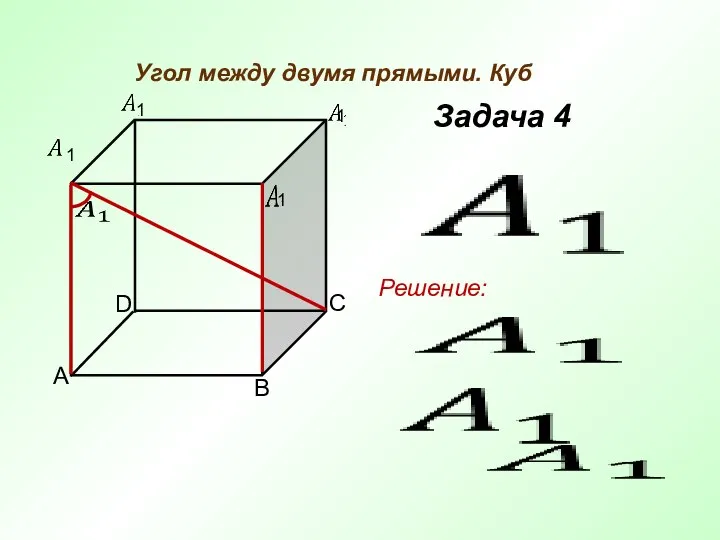
- 7. Угол между двумя прямыми. Куб Задача 4 Решение: 1 1 1 1
- 8. Повторяем теорию: Как находят координаты вектора, если известны координаты его начала и конца? Как находят координаты
- 9. Повторяем теорию: Какие векторы называются перпендикулярными? Что называется скалярным произведением векторов? Чему равно скалярное произведение перпендикулярных
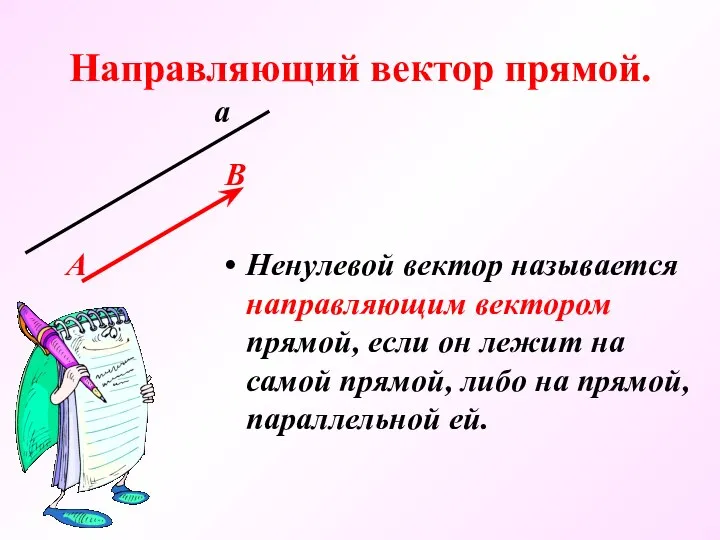
- 10. Направляющий вектор прямой. Ненулевой вектор называется направляющим вектором прямой, если он лежит на самой прямой, либо
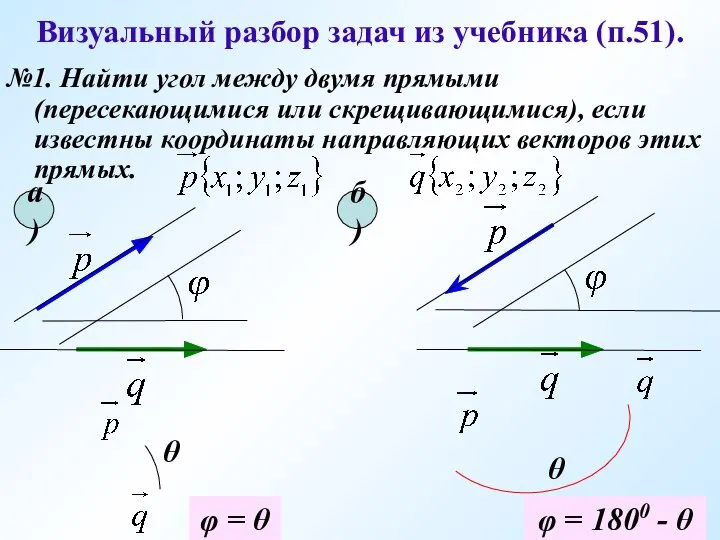
- 11. Визуальный разбор задач из учебника (п.51). №1. Найти угол между двумя прямыми (пересекающимися или скрещивающимися), если
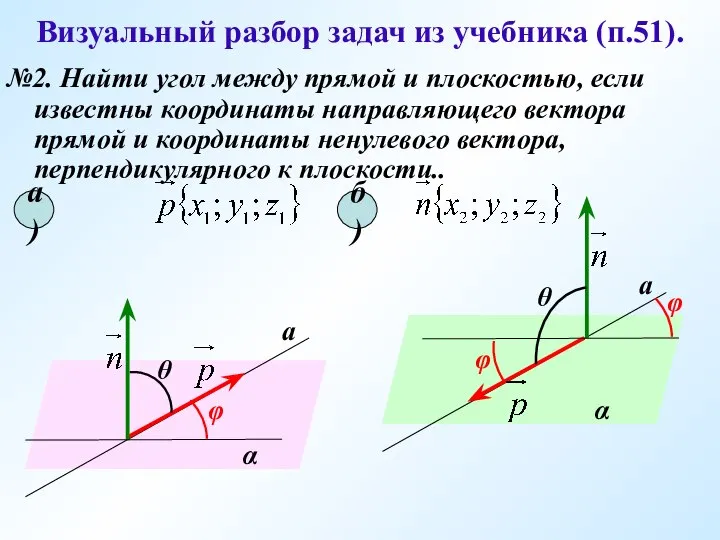
- 12. Визуальный разбор задач из учебника (п.51). №2. Найти угол между прямой и плоскостью, если известны координаты
- 13. № 464 (а) Дано: Найти: угол между прямыми АВ и CD. Ваши предложения… Найдем координаты векторов
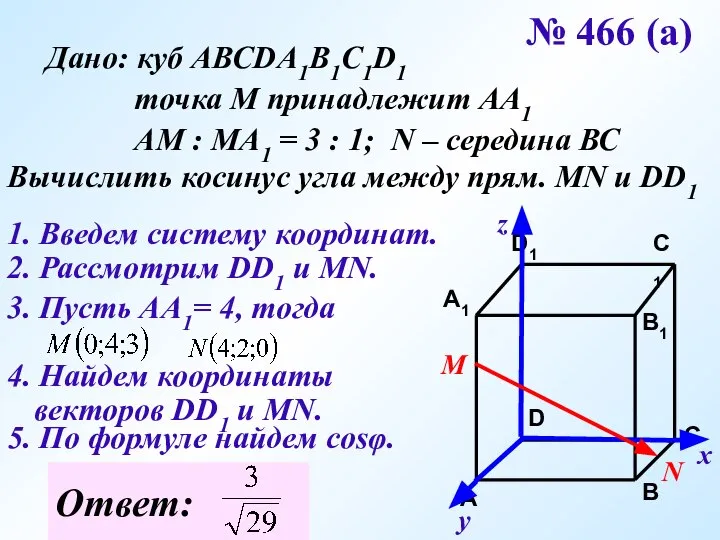
- 14. № 466 (а) Дано: куб АВСDA1B1C1D1 точка М принадлежит АА1 АМ : МА1 = 3 :
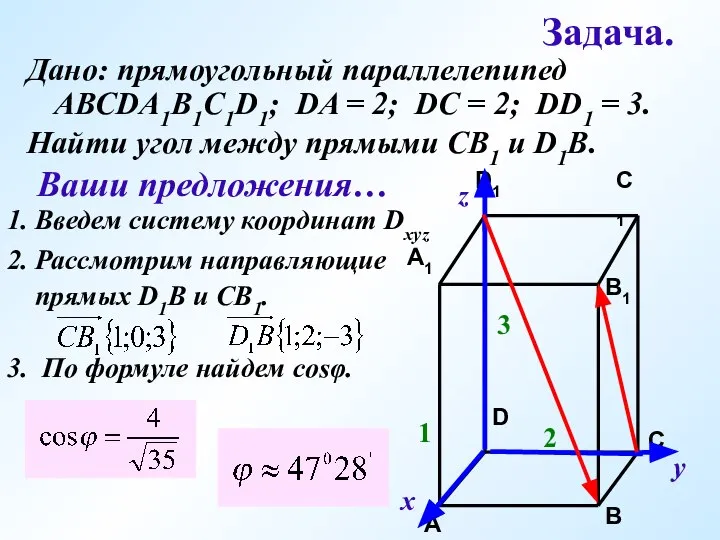
- 15. Задача. Дано: прямоугольный параллелепипед АВСDA1B1C1D1; DA = 2; DC = 2; DD1 = 3. 1 2
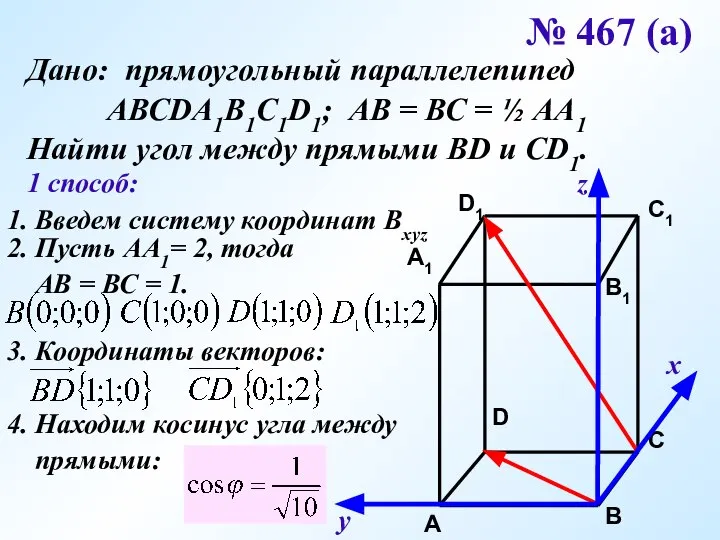
- 16. № 467 (а) Дано: прямоугольный параллелепипед АВСDA1B1C1D1; АВ = ВС = ½ АА1 Найти угол между
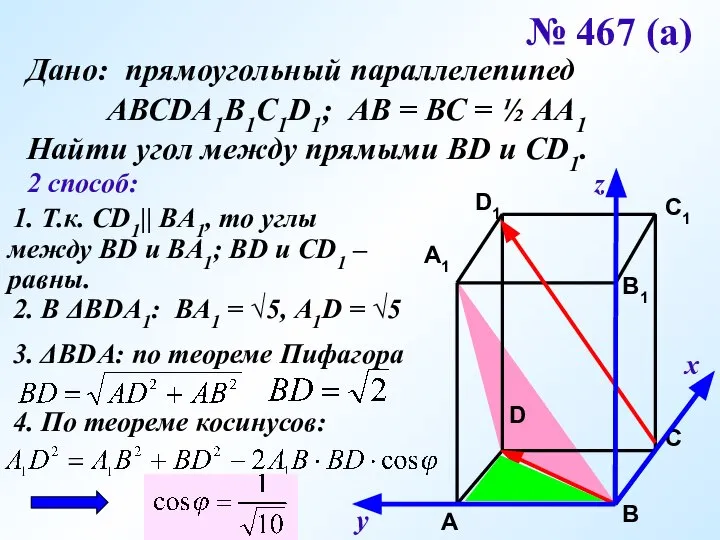
- 17. х у z № 467 (а) Дано: прямоугольный параллелепипед АВСDA1B1C1D1; АВ = ВС = ½ АА1
- 18. п. 52, №464 (б, в, г) №466 (б, в) Домашнее задание:
- 20. Скачать презентацию






 В мире цветов и плодов. Интегрированный урок биологии и математики
В мире цветов и плодов. Интегрированный урок биологии и математики Презентация на тему Лобачевский Николай Иванович
Презентация на тему Лобачевский Николай Иванович  Обыкновенная дробь
Обыкновенная дробь Формирование математических представлений, умений и навыков у дошкольников
Формирование математических представлений, умений и навыков у дошкольников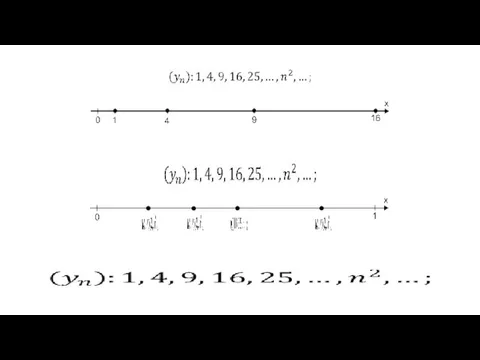 Пояснения к определению предела последовательности
Пояснения к определению предела последовательности Производная функции
Производная функции Математический тренажёр Бабушкины примеры
Математический тренажёр Бабушкины примеры Презентация по математике "Число 5. Цифра 5" -
Презентация по математике "Число 5. Цифра 5" -  Выражение (для печатной и электронной формы учебника)
Выражение (для печатной и электронной формы учебника) Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Применение производной в географии. 10 класса
Применение производной в географии. 10 класса Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  32046
32046 Что будет со мной, если буду питаться, как Дюймовочка?
Что будет со мной, если буду питаться, как Дюймовочка? Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Презентация на тему Сравнение предметов по различным признакам
Презентация на тему Сравнение предметов по различным признакам  Площадь треугольника
Площадь треугольника Дифференциальные уравнения
Дифференциальные уравнения Урок математики в 4 классе по системе Л.В.Занкова (1-4) «Действия с многозначными числами» Автор: Каграманян Елена Владимировна, учи
Урок математики в 4 классе по системе Л.В.Занкова (1-4) «Действия с многозначными числами» Автор: Каграманян Елена Владимировна, учи МВ УРОК 22 ГЕО ТРЕУГОЛЬНИК
МВ УРОК 22 ГЕО ТРЕУГОЛЬНИК Площадь фигур - какие они
Площадь фигур - какие они 8637
8637 Комбинаторика. Комбинаторные объекты
Комбинаторика. Комбинаторные объекты Проценты (5 класс)
Проценты (5 класс) Презентация на тему Викторина "Ох уж эта математика" 5 класс
Презентация на тему Викторина "Ох уж эта математика" 5 класс  ОГЭ. Приемы решения практико-ориентированных задач
ОГЭ. Приемы решения практико-ориентированных задач Множення і ділення звичайних дробів
Множення і ділення звичайних дробів