Содержание
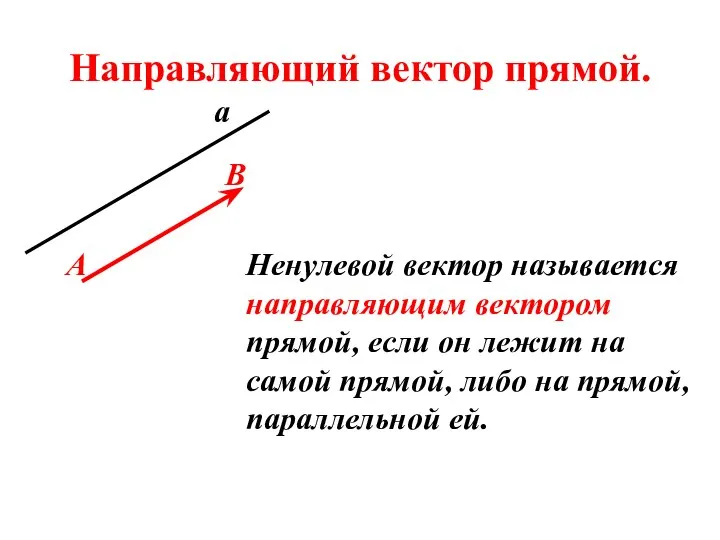
- 2. Направляющий вектор прямой. Ненулевой вектор называется направляющим вектором прямой, если он лежит на самой прямой, либо
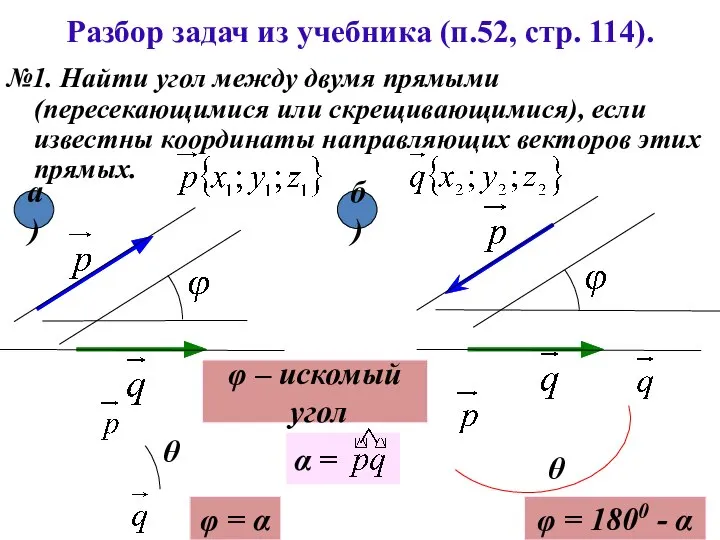
- 3. Разбор задач из учебника (п.52, стр. 114). №1. Найти угол между двумя прямыми (пересекающимися или скрещивающимися),
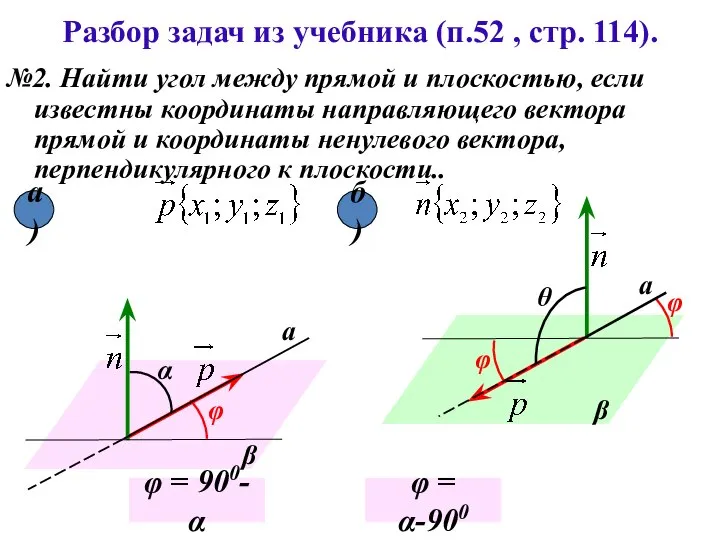
- 4. Разбор задач из учебника (п.52 , стр. 114). №2. Найти угол между прямой и плоскостью, если
- 5. № 464 (а) Дано: Найти: угол между прямыми АВ и CD. Найдем координаты векторов 2. Воспользуемся
- 6. §3. Движение. Виды движения. Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками.
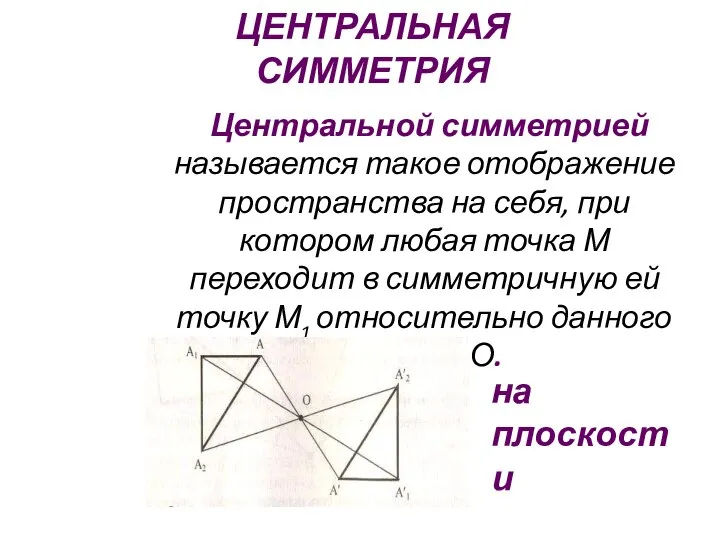
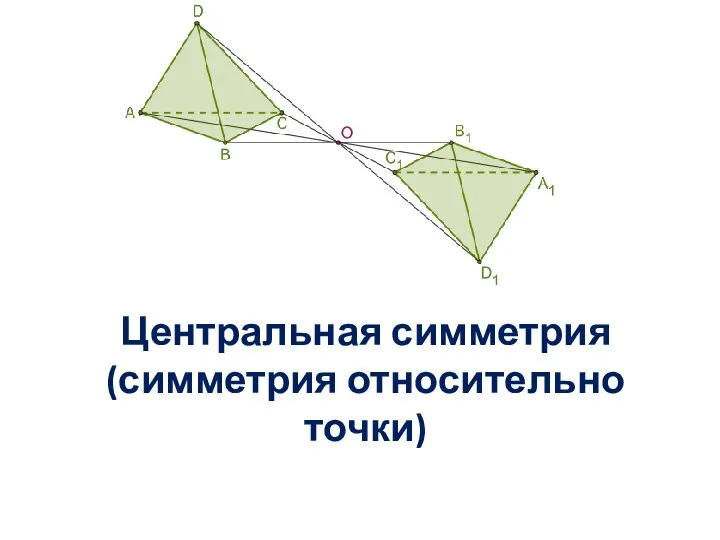
- 7. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Центральной симметрией называется такое отображение пространства на себя, при котором любая точка М переходит
- 8. Центральная симметрия (симметрия относительно точки)
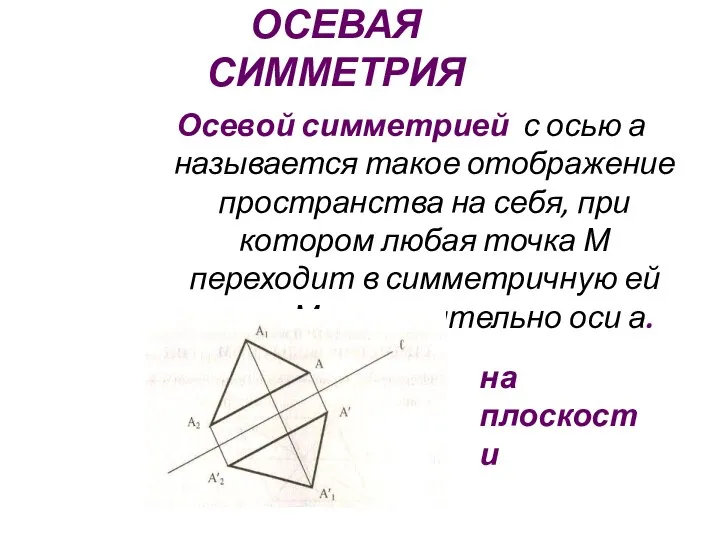
- 9. ОСЕВАЯ СИММЕТРИЯ Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая
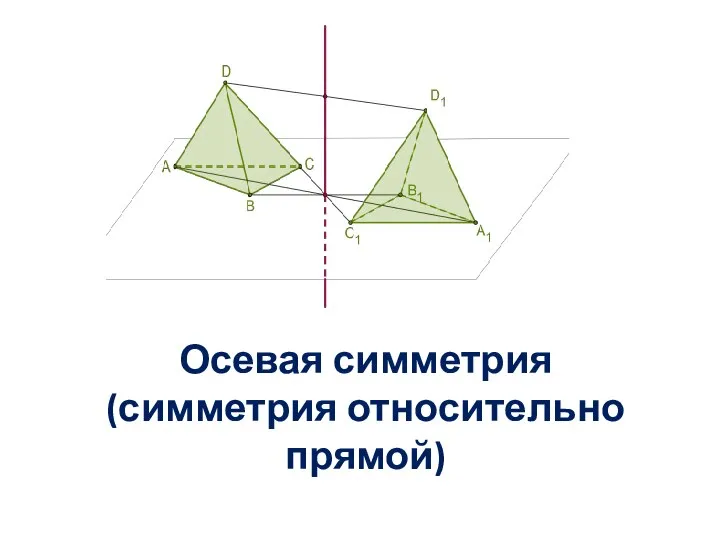
- 10. Осевая симметрия (симметрия относительно прямой)
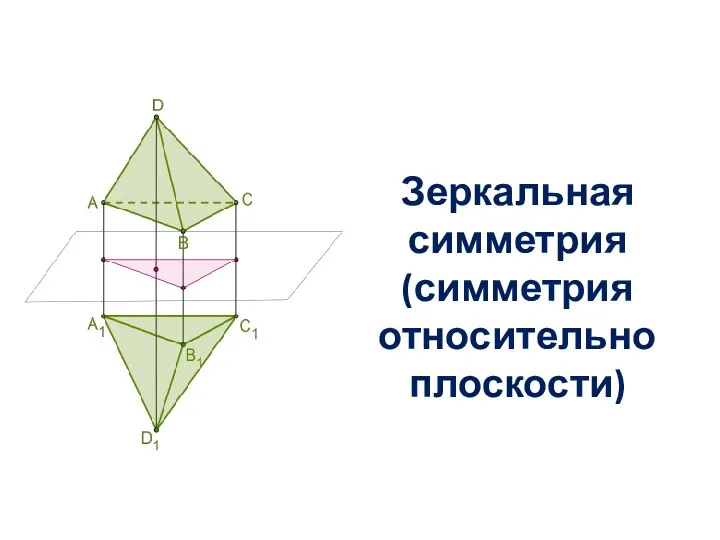
- 11. ЗЕРКАЛЬНАЯ СИММЕТРИЯ ЗЕРКАЛЬНОЙ СИММЕТРИЕЙ - называется такое отображение пространства на себя, при котором любая точка М
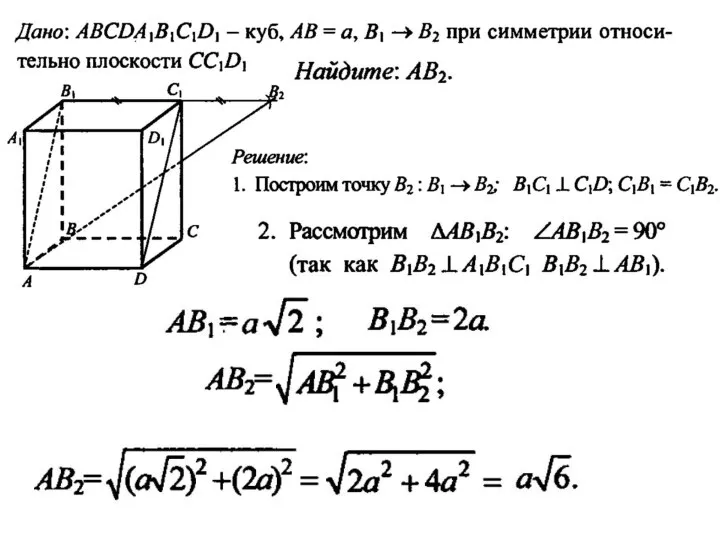
- 12. Зеркальная симметрия (симметрия относительно плоскости)
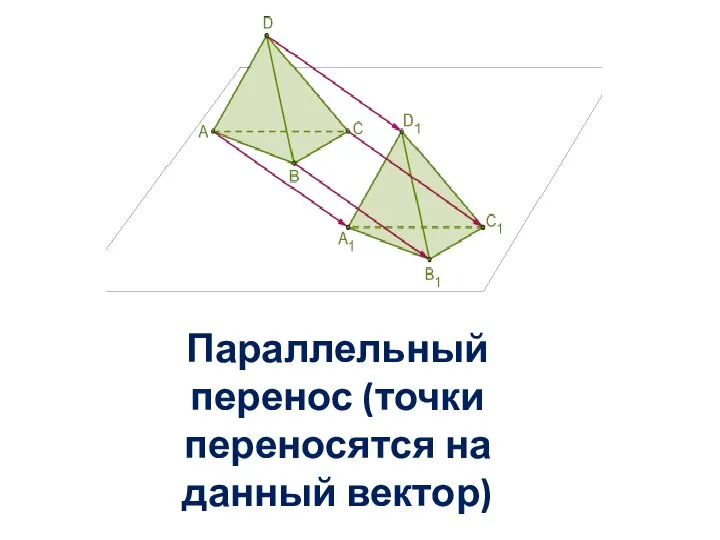
- 13. ПАРАЛЛЕЛЬНЫЙ Перенос Параллельным переносом на вектор называется отображение пространства на себя, при котором любая точка М
- 14. Параллельный перенос (точки переносятся на данный вектор)
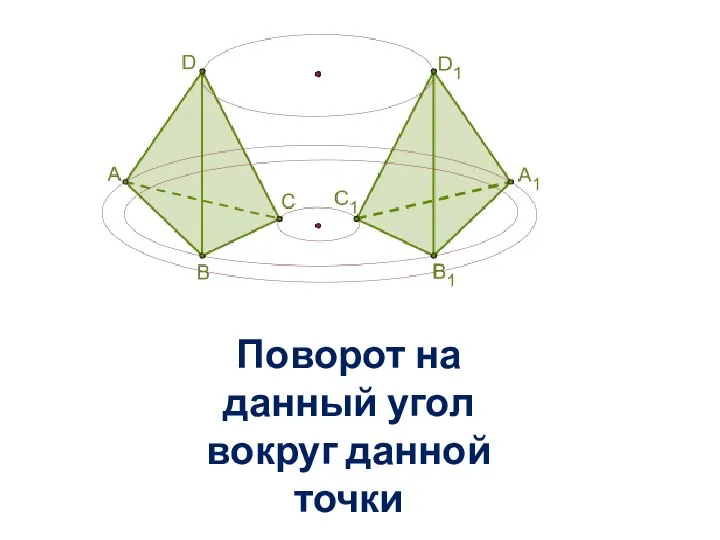
- 15. ПОВОРОТ Преобразование, при котором каждая точка пространства поворачивается на один и тот же угол α вокруг
- 16. Поворот на данный угол вокруг данной точки
- 17. ДОМА § 3, № 478(б, в)
- 19. СИММЕТРИЯ В РАСТЕНИЯХ Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия. Ярко
- 20. СИММЕТРИЯ В ЖИВОТНОМ МИРЕ Симметрия встречается и в животном мире. Однако в отличие от мира растений
- 22. Скачать презентацию








 Знакомство с числами
Знакомство с числами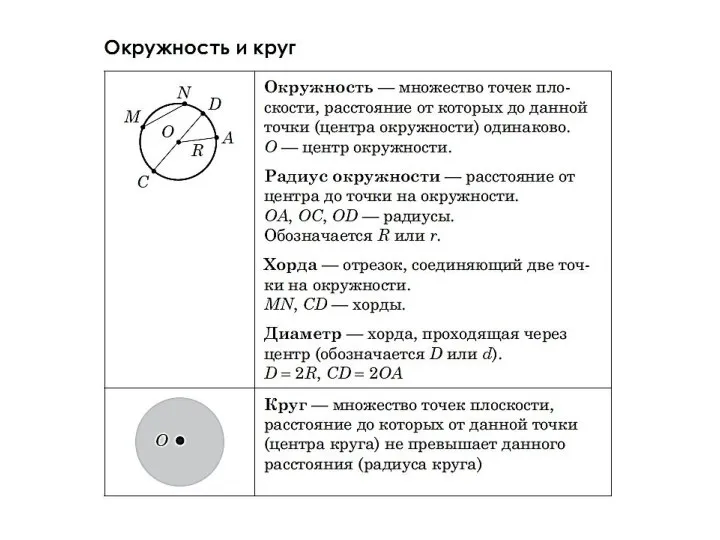 Окружность и круг
Окружность и круг Определение степени готовности объектов НКИ к применению. Тема 17
Определение степени готовности объектов НКИ к применению. Тема 17 Задача на внимание. 5 класс
Задача на внимание. 5 класс Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Цели урока:
Цели урока: Площади геометрических фигур
Площади геометрических фигур Геометрический смысл производной. Решение примеров на геометрический смысл производной
Геометрический смысл производной. Решение примеров на геометрический смысл производной 08.09
08.09 Арифметический диктант
Арифметический диктант Умножение дробей
Умножение дробей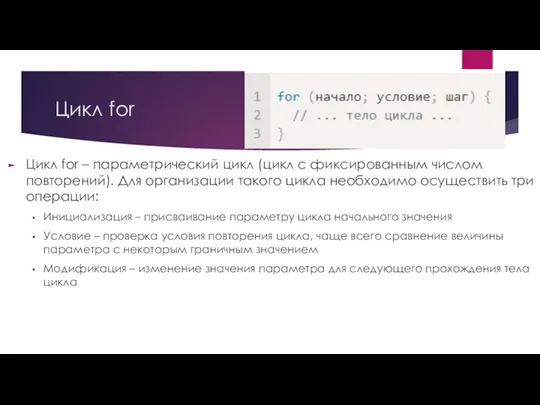 Цикл for
Цикл for Задачи на движение
Задачи на движение Закрепление таблицы умножения и деления
Закрепление таблицы умножения и деления Распределительное свойство
Распределительное свойство Сравнение дробей
Сравнение дробей Арифметика в позиционных системах счисления
Арифметика в позиционных системах счисления Glava_5_-_Proektirovanie_vyborki_Gubko_A_M
Glava_5_-_Proektirovanie_vyborki_Gubko_A_M Дидактический материал. Проверочные работы. Начальные понятия геометрии
Дидактический материал. Проверочные работы. Начальные понятия геометрии Презентация на тему Построение правильного шестиугольника
Презентация на тему Построение правильного шестиугольника  Проценты. Определение, обозначение, вычисление, применение Математика 5 класс
Проценты. Определение, обозначение, вычисление, применение Математика 5 класс Центральная симметрия
Центральная симметрия Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Арифметический корень степени п
Арифметический корень степени п ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Многоугольники в нашей жизни
Многоугольники в нашей жизни Математика и мир искусства
Математика и мир искусства