Содержание
- 9. Правильный шестиугольник
- 18. Равносторонний треугольник Осями симметрии равностороннего треугольника являются биссектрисы его углов. Поделить угол пополам поможет транспортир или
- 21. Рассмотрим решение задачи вырезания из листа бумаги квадрата и правильного шестиугольника, используя другие оси симметрии этих
- 24. Правильный шестиугольник.
- 27. Чтобы вырезать из листа бумаги в виде дыры правильный многоугольник одним разрезом, достаточно провести оси симметрии
- 28. Разносторонний треугольник
- 36. Теорема сгибания и вырезания Теорема: любую форму с прямыми сторонами можно вырезать из одного (идеализированного) листа
- 37. 1. Метод поиска прямого скелета
- 38. Прямолинейный скелет многоугольника (straight skeleton) - набор линий, который образуется вершинами многоугольника при их движении с
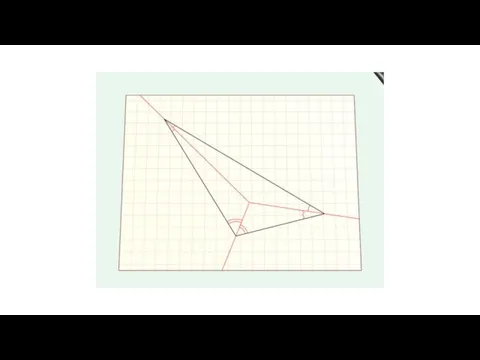
- 39. Применим метод поиска прямого скелета для вырезания произвольного четырехугольника Проводим из каждого угла биссектрисы до их
- 41. По свойству точки пересечения биссектрис получаем по три равных перпендикуляра Следовательно, треугольники 1=2, 3=4,5=6,7=8.
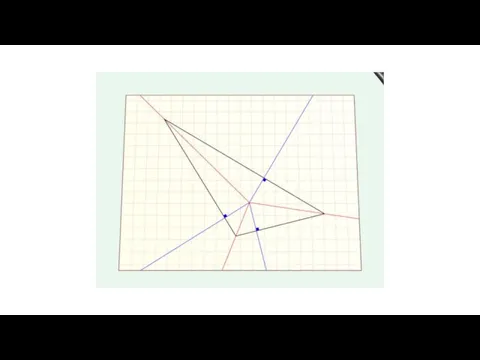
- 42. Соединим точки пересечения биссектрис. Четырехугольники 9 и 10 равны. Биссектрисы и соединяющий их отрезок образуют скелет
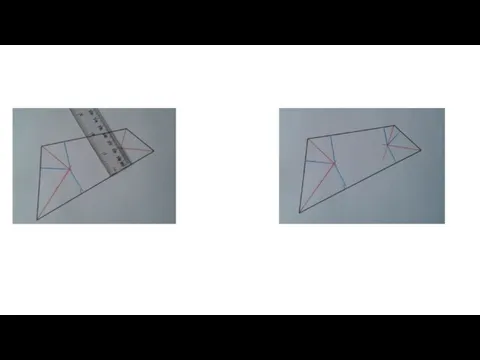
- 43. В результате построений получили пары равных фигур – треугольников и четырехугольников. Начинаем складывать по скелету. Затем
- 45. Скачать презентацию







































 Вычисление площадей и объемов при помощи определенных интегралов. 7 Занятие
Вычисление площадей и объемов при помощи определенных интегралов. 7 Занятие Логика. Задания
Логика. Задания Косвенные измерения
Косвенные измерения Таблица сложения в пределах 20
Таблица сложения в пределах 20 Пропорциональность площадей
Пропорциональность площадей Выбор математической модели воздушного винта для оценки его влияния на аэродинамические характеристики летательного аппарата
Выбор математической модели воздушного винта для оценки его влияния на аэродинамические характеристики летательного аппарата По Щучьему велению на новый лад
По Щучьему велению на новый лад Группа предметов. Множество. Элемент множества. 3 класс
Группа предметов. Множество. Элемент множества. 3 класс Интегрированный урок на закрепление знаний по математике, биологии с применением информационных технологий. Можно создавать тес
Интегрированный урок на закрепление знаний по математике, биологии с применением информационных технологий. Можно создавать тес Прямоугольный треугольник
Прямоугольный треугольник Движение по реке. Водный транспорт
Движение по реке. Водный транспорт Презентация на тему Системы уравнений
Презентация на тему Системы уравнений  Симметрия
Симметрия 1_1_matritsy (1)
1_1_matritsy (1) Задачи на деление по содержанию и деление на равные доли
Задачи на деление по содержанию и деление на равные доли Десятичные дроби
Десятичные дроби Теорема Пифагора
Теорема Пифагора Параллельность плоскостей определение
Параллельность плоскостей определение Классная работа по математике
Классная работа по математике Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Задание 2 по математике
Задание 2 по математике Динамика системы вблизи цикла
Динамика системы вблизи цикла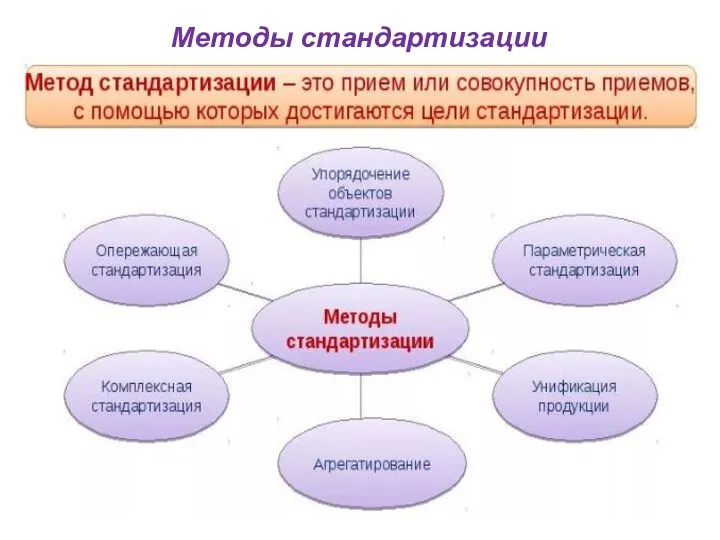 Методы стандартизации. Упорядочение объектов стандартизации (лекция 2)
Методы стандартизации. Упорядочение объектов стандартизации (лекция 2) Сложение смешанных дробей
Сложение смешанных дробей Презентация на тему Векторы
Презентация на тему Векторы  Число и цифра 5
Число и цифра 5 Основы оптимального проектирования
Основы оптимального проектирования Краткая история появления и развития пределов
Краткая история появления и развития пределов