Содержание
- 2. Цільова функція Обмеження (2) (3) (4) Математична модель ЗЦЛП
- 3. Один з найпростіших підходів до вирішення ЗЦЛП: вирішити неперервну задачу (ЗЛП) округлити координати отриманого оптимуму до
- 4. Один з найпростіших підходів до вирішення ЗЦЛП: вирішити неперервну задачу (ЗЛП) округлити координати отриманого оптимуму до
- 5. Випадок 1 Серед вихідних обмежень є обмеження-рівності. В цьому випадку округлений розв’язок (майже) завжди є недопустимим
- 6. Проблеми, що виникають при округленні розв’язку ЗЛП (2)
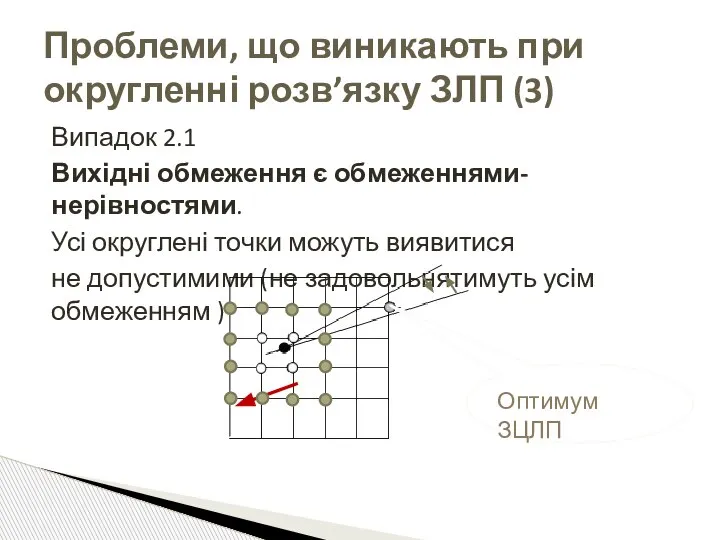
- 7. Випадок 2.1 Вихідні обмеження є обмеженнями-нерівностями. Усі округлені точки можуть виявитися не допустимими (не задовольнятимуть усім
- 8. Випадок 2.1 Вихідні обмеження є обмеженнями-нерівностями. Усі округлені точки можуть виявитися не допустимими (не задовольнятимуть усім
- 9. Випадок 2.2 Вихідні обмеження є обмеженнями-нерівностями. Округлена допустима точка може виявитися не оптимальною. Приклад Проблеми, що
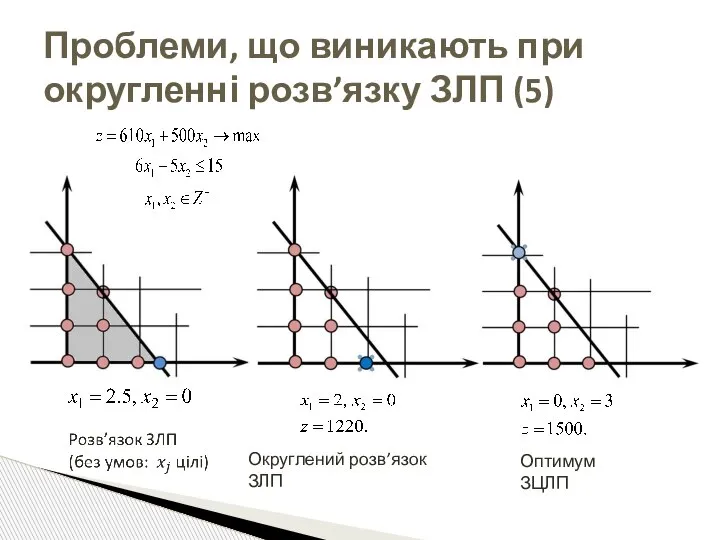
- 10. Проблеми, що виникають при округленні розв’язку ЗЛП (5) Округлений розв’язок ЗЛП Оптимум ЗЦЛП
- 11. Методи відсікань Гоморі Метод гілок та меж Методи розв’язання ЗЦЛП
- 12. Алгоритм Гоморі Дослідження операцій
- 13. Цільова функція Обмеження (2) (3) (4) Математична модель ЗЦЛП Існує принципова можливість звести розв’язання ЗЦЛП (1)
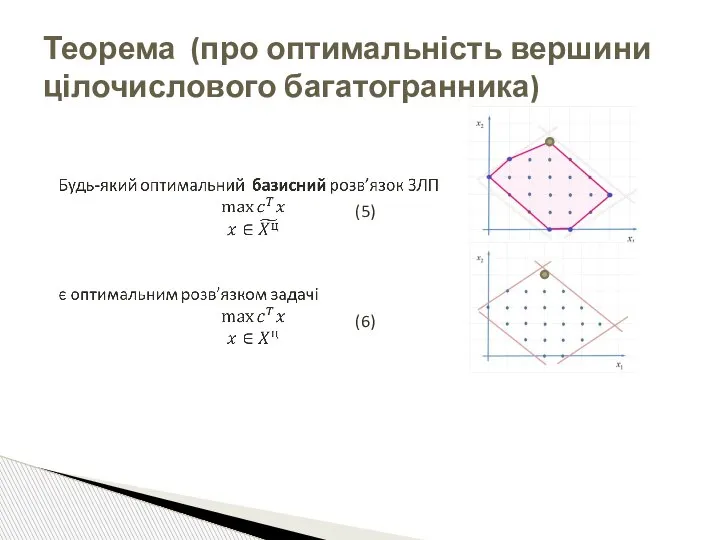
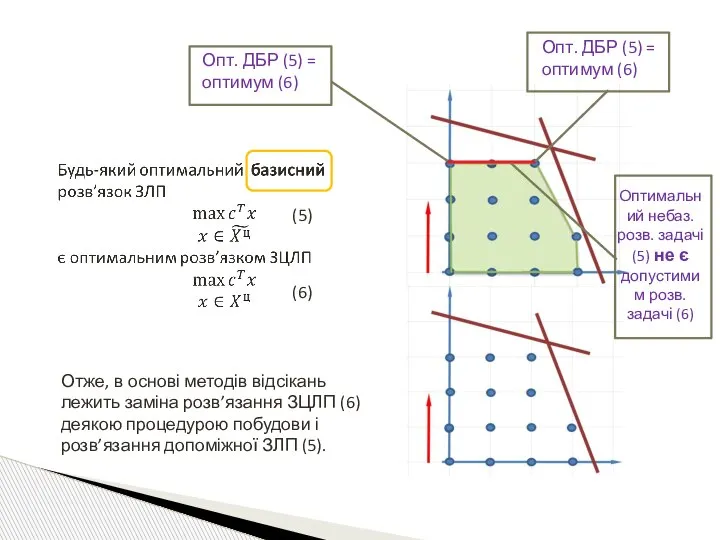
- 16. Теорема (про оптимальність вершини цілочислового багатогранника) (5) (6)
- 17. Доказательство теоремы (1) (5) (6)
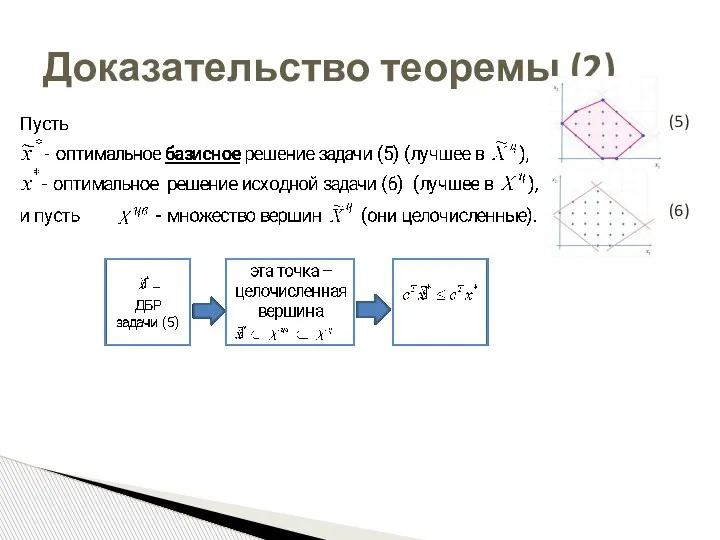
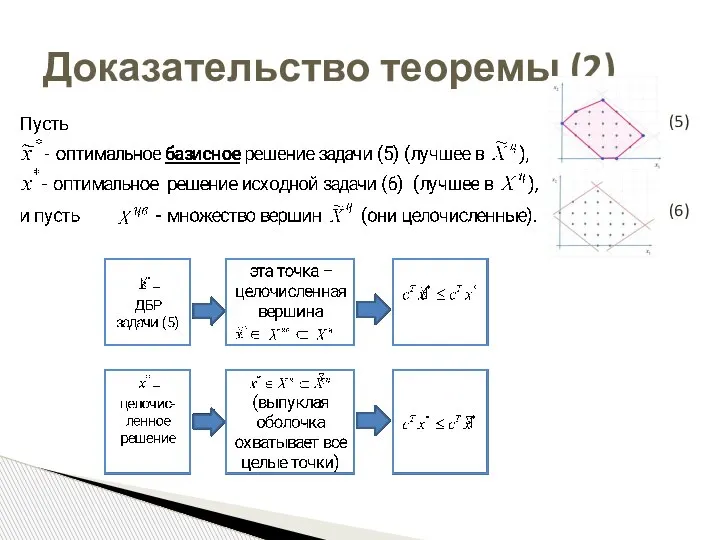
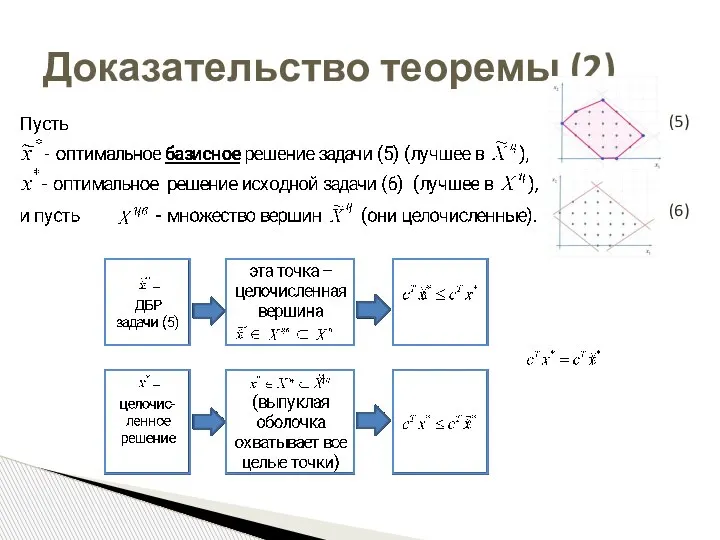
- 18. Доказательство теоремы (2) (5) (6)
- 19. Доказательство теоремы (2) (5) (6)
- 20. Доказательство теоремы (2) (5) (6)
- 21. Отже, в основі методів відсікань лежить заміна розв’язання ЗЦЛП (6) деякою процедурою побудови і розв’язання допоміжної
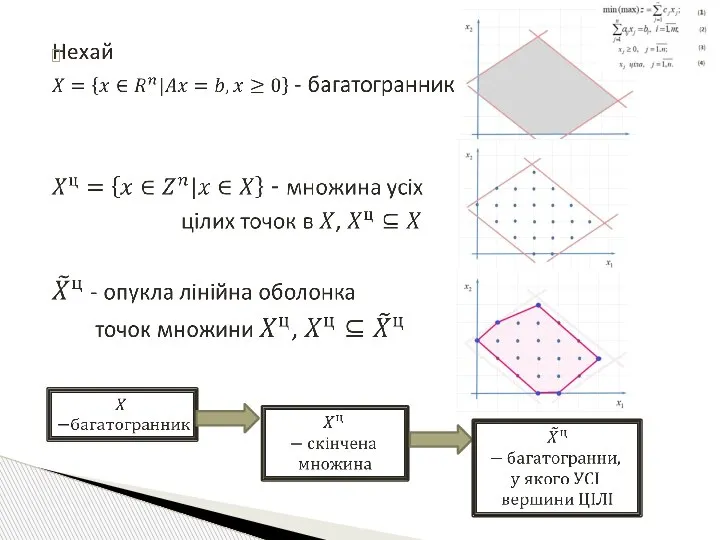
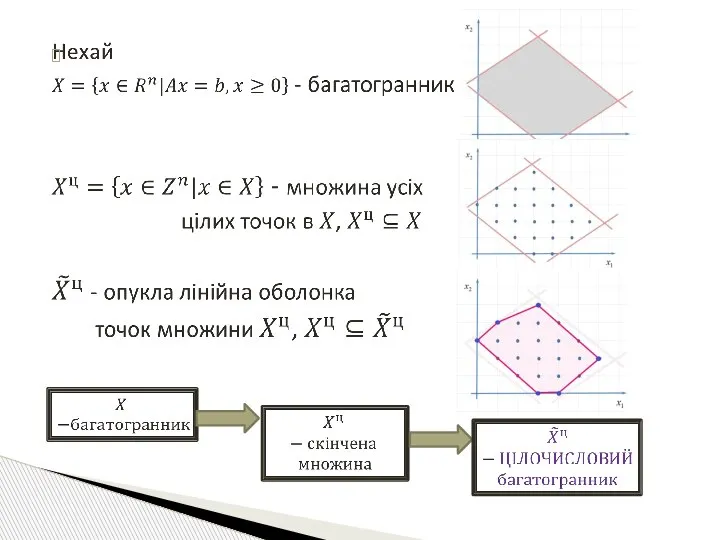
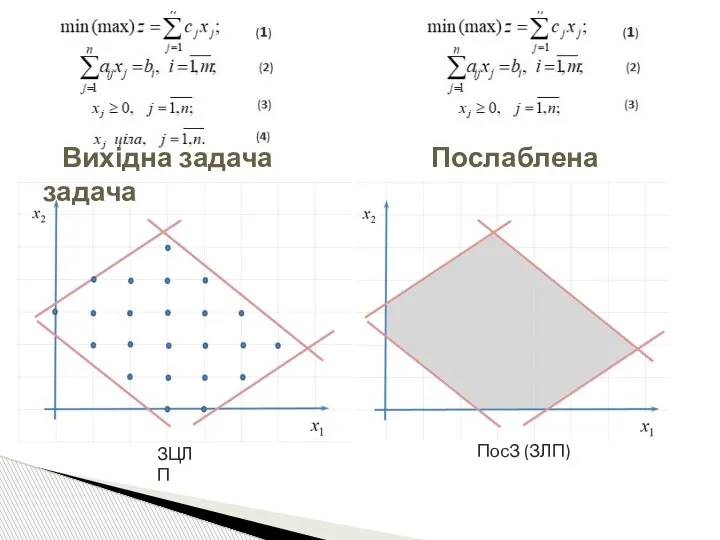
- 22. Визначення. Послабленою називається задача ЛП, яка отримана з ЗЦЛП шляхом відкидання умов цілочисловості. Властивості ПосЗ 1)
- 23. ЗЦЛП ПосЗ (ЗЛП) Вихідна задача Послаблена задача
- 24. 1) Вихідною точкою є оптимальний розв’язок відповідної послабленої задачі. 2) На кожній ітерації додається лінійне обмеження,
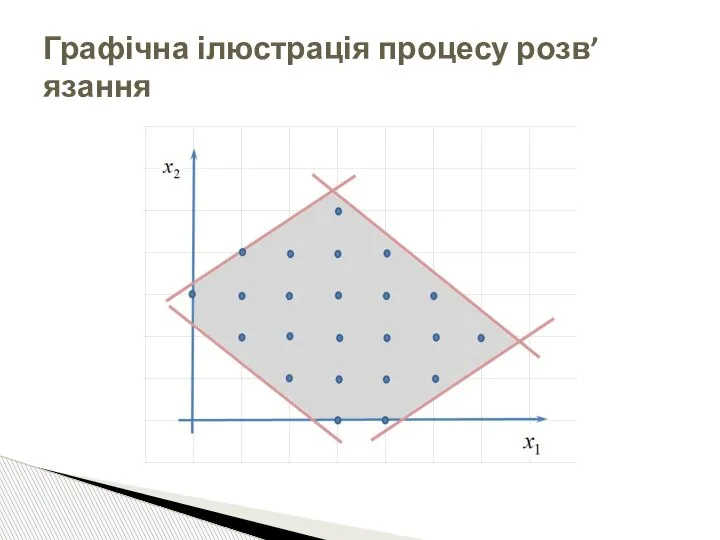
- 25. Графічна ілюстрація процесу розв’язання
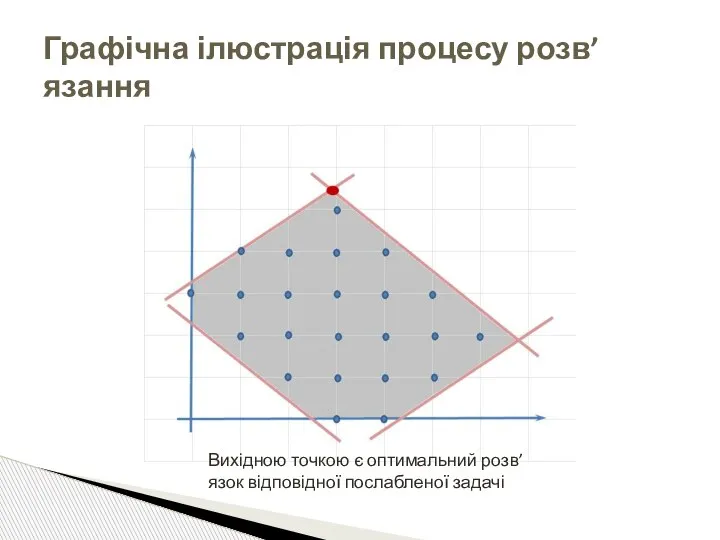
- 26. Графічна ілюстрація процесу розв’язання Вихідною точкою є оптимальний розв’язок відповідної послабленої задачі
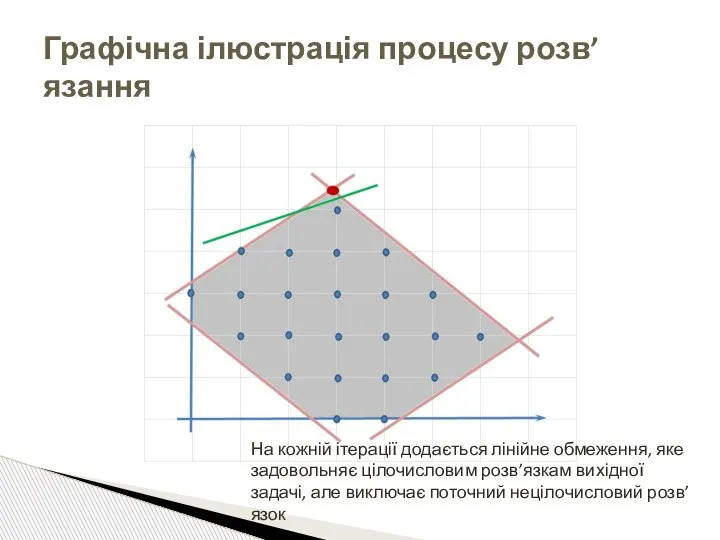
- 27. Графічна ілюстрація процесу розв’язання На кожній ітерації додається лінійне обмеження, яке задовольняє цілочисловим розв’язкам вихідної задачі,
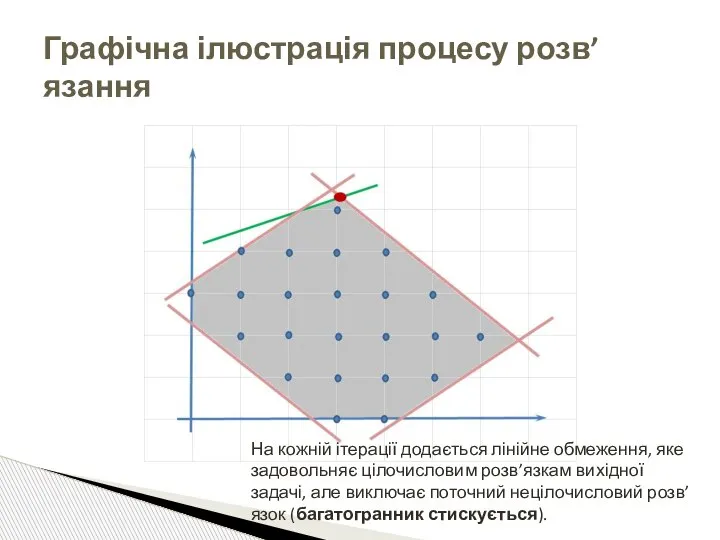
- 28. Графічна ілюстрація процесу розв’язання На кожній ітерації додається лінійне обмеження, яке задовольняє цілочисловим розв’язкам вихідної задачі,
- 29. Графічна ілюстрація процесу розв’язання
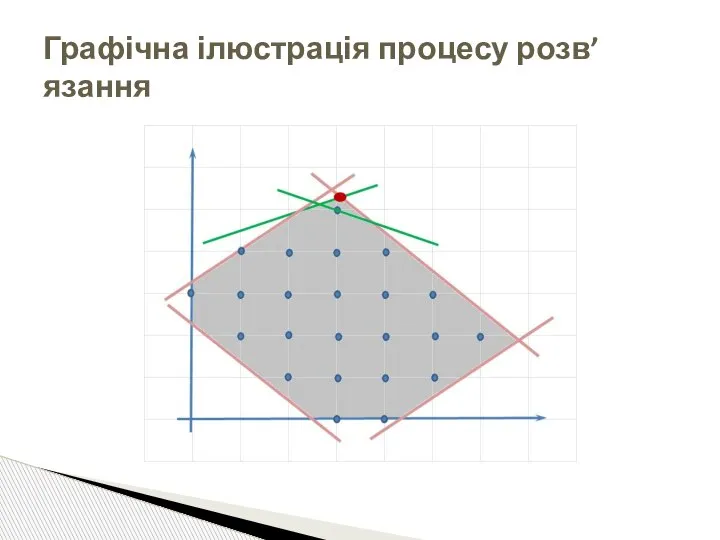
- 30. Графічна ілюстрація процесу розв’язання
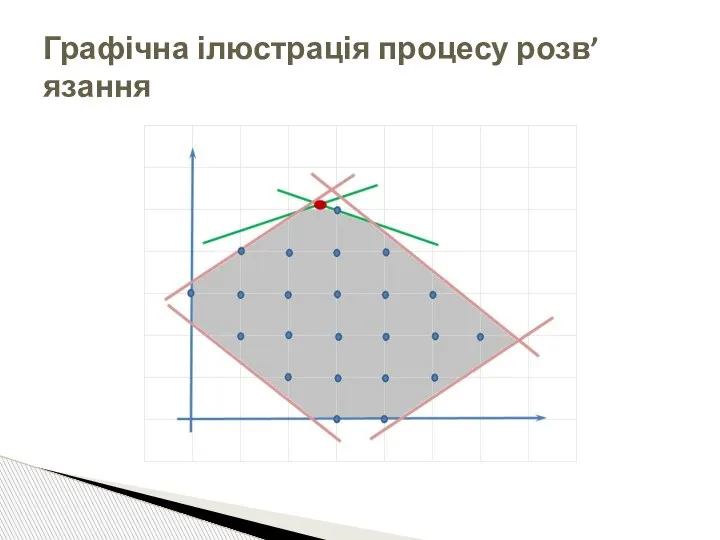
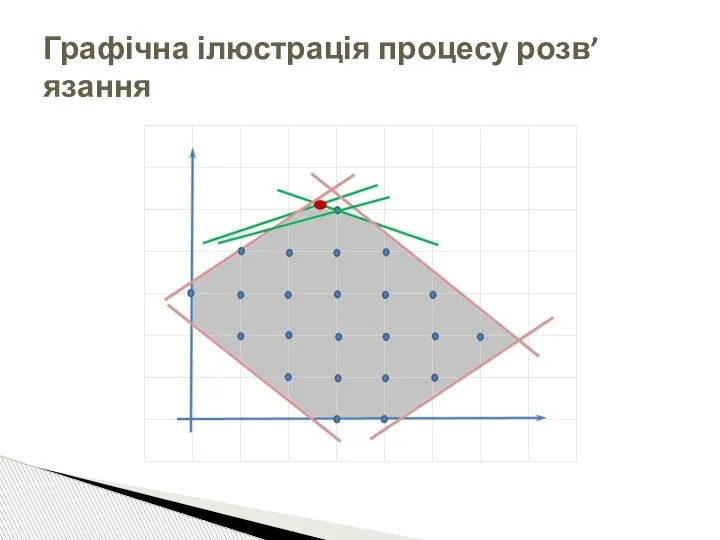
- 31. Графічна ілюстрація процесу розв’язання
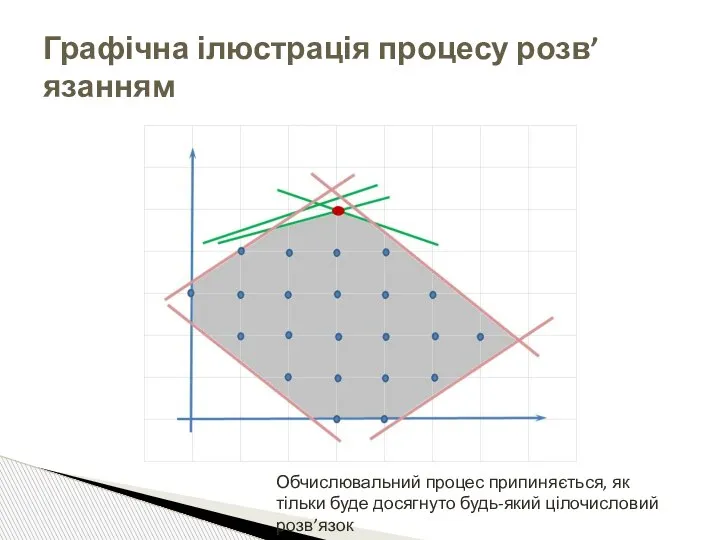
- 32. Графічна ілюстрація процесу розв’язанням Обчислювальний процес припиняється, як тільки буде досягнуто будь-який цілочисловий розв’язок
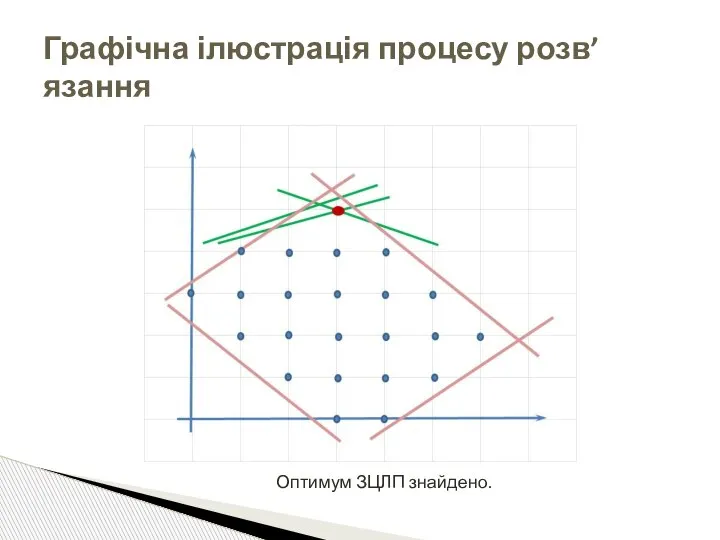
- 33. Графічна ілюстрація процесу розв’язання Оптимум ЗЦЛП знайдено.
- 34. Метод відсікань для розв’язання повністю цілочислових задач Метод відсікань для розв’язання частково цілочислових задач Будемо розглядати
- 35. ЗЦЛП
- 36. Приклад Канонічна форма ЗЦЛП
- 37. Початковий крок Спочатку розв’язуємо послаблену задачу. Якщо її розв’язок цілочисловий, то він же є і розв’язком
- 38. 1) знаходження універсального правила формування додаткових обмежень; 2) доведення скінченності відповідного процесу відсікання; 3) боротьба з
- 39. Як побудувати додаткове лінійне обмеження, якому задовольняє кожний розв’язок, допустимий за умовами (2) - (4)? Виведення
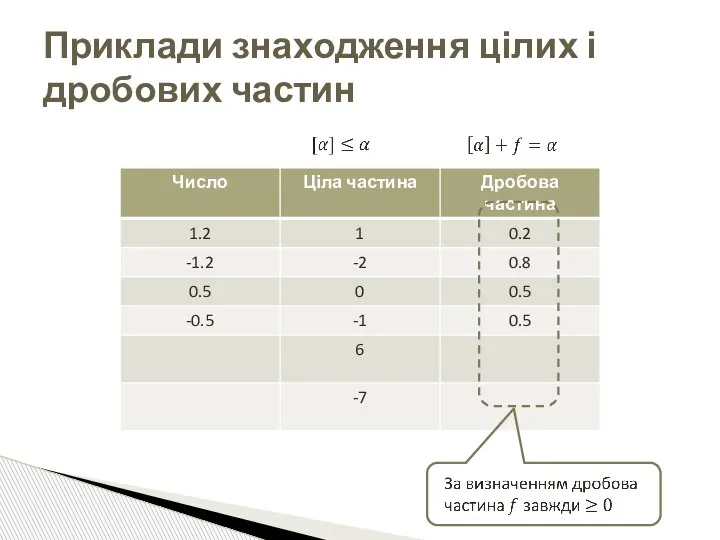
- 40. Виведення рівняння-відсікання Символом [α] позначатимемо цілу частину дійсного числа α: найбільше ціле, менше або рівне за
- 41. Приклади знаходження цілих і дробових частин
- 42. Визначення Рівняння в дробових частинах називається рівнянням відсікання (відсіканням Гоморі) Рівняння (7), за яким побудували рівняння
- 43. Схема алгоритму Гоморі
- 44. Формування рівняння-відсікання
- 45. Формування рівняння-відсікання
- 46. Формування рівняння-відсікання
- 47. Формування рівняння-відсікання Рівняння в цілих частинах Рівняння відсікання (саме його додаємо до оптимальної симплекс-таблиці ПосЗ)
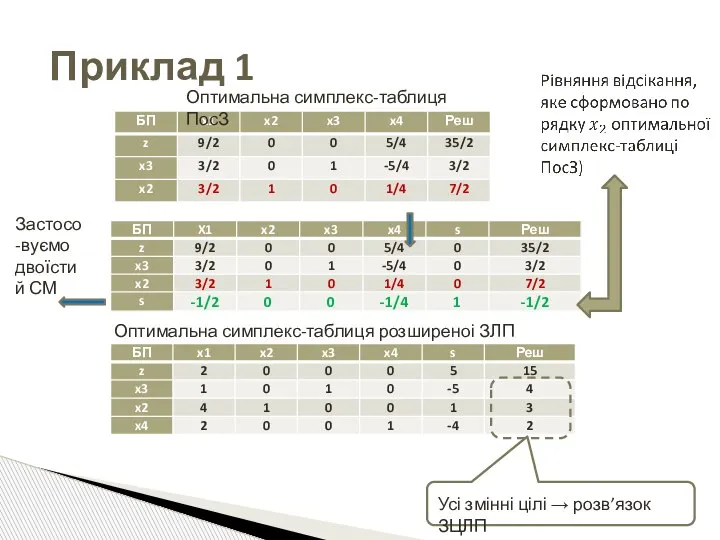
- 48. Приклад 1 Оптимальна симплекс-таблиця ПосЗ Оптимальна симплекс-таблиця розширеноі ЗЛП Застосо-вуємо двоїстий СМ
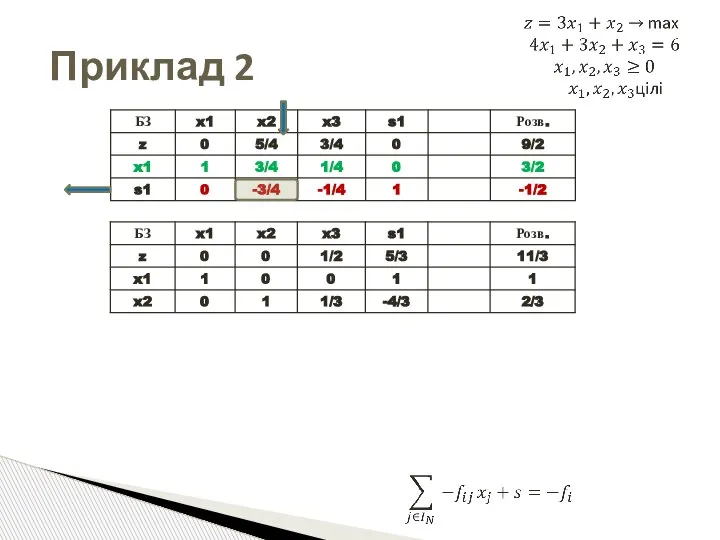
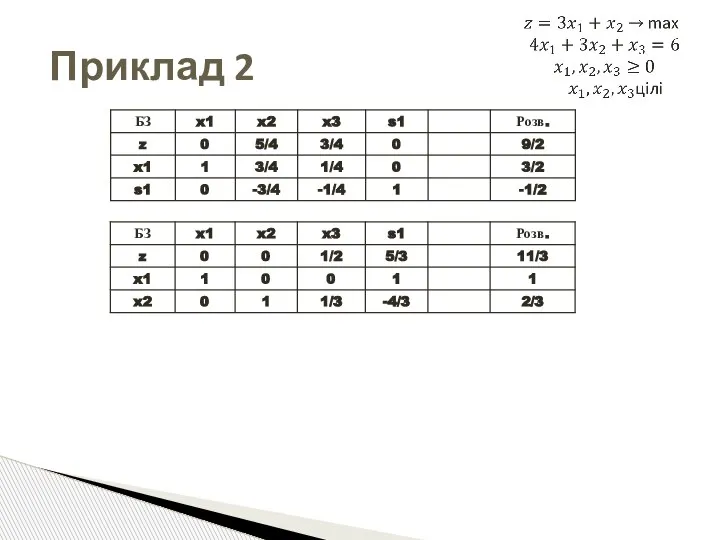
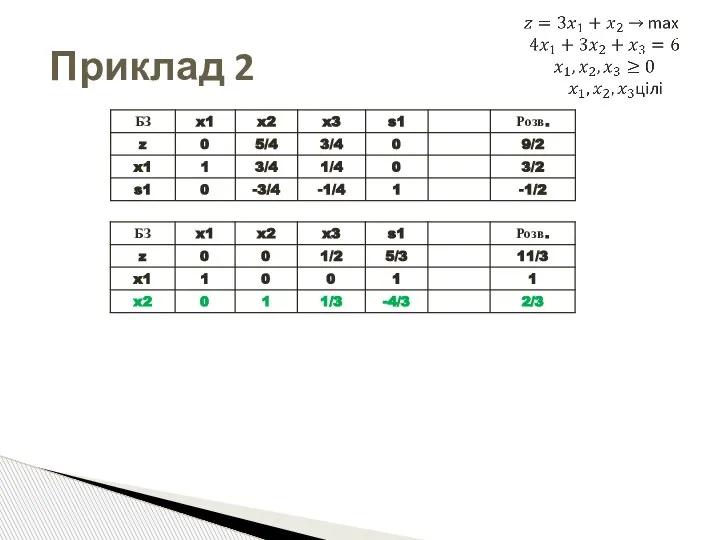
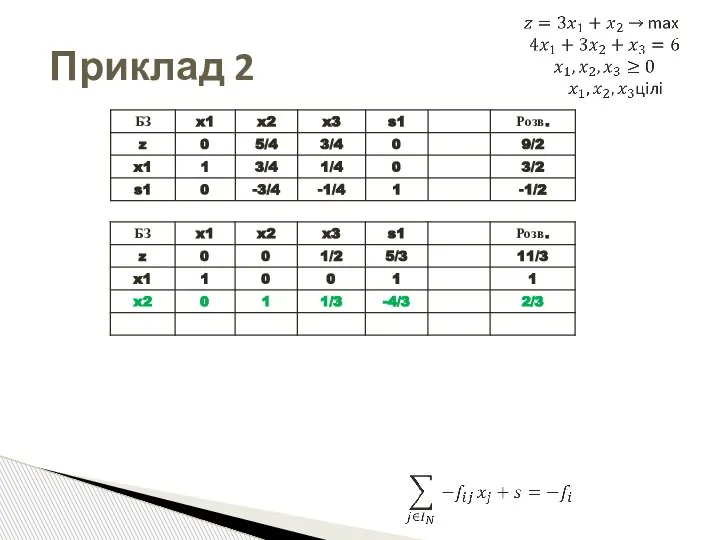
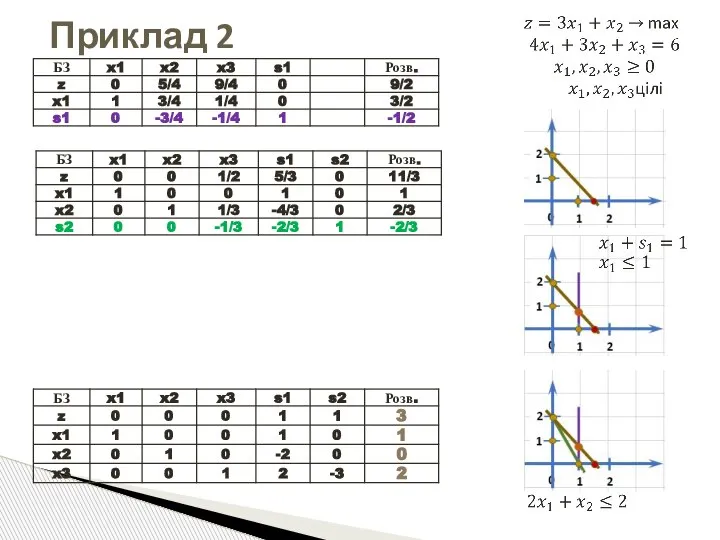
- 49. Приклад 2 Оптимальна симплекс-таблиця ПосЗ
- 50. Приклад 2
- 51. Приклад 2
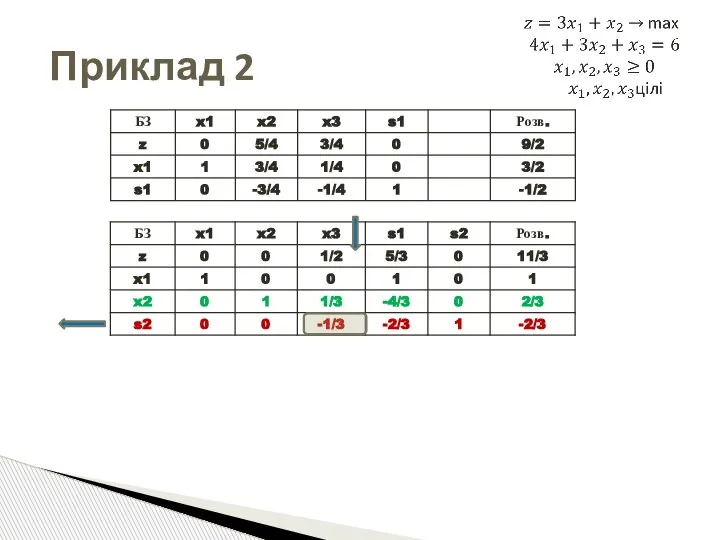
- 52. Приклад 2
- 53. Приклад 2
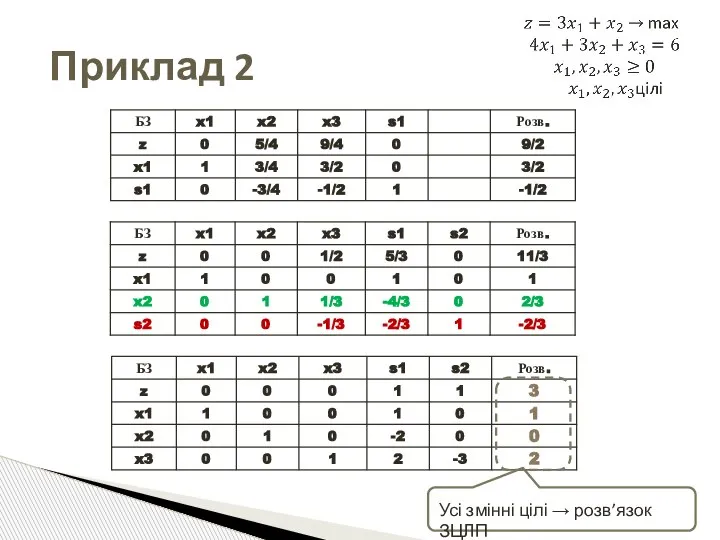
- 54. Приклад 2
- 55. Приклад 2
- 56. Приклад 2
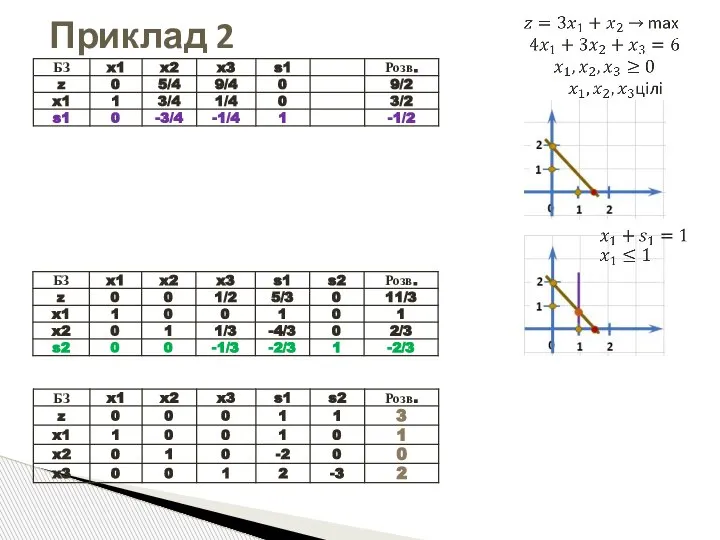
- 57. Графічна ілюстрація Приклад 2
- 58. Приклад 2
- 59. Приклад 2
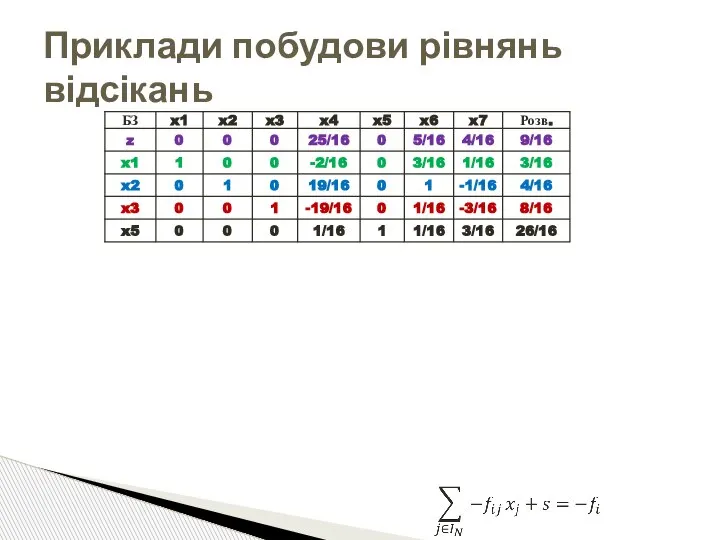
- 60. Приклади побудови рівнянь відсікань
- 61. Про розмір розширеної задачі ЗЦЛП ЗЛП
- 62. Про розмір розширеної задачі (РЗ) РЗ – розширена задача
- 63. Про розмір розширеної задачі
- 64. Ефективність відсікань
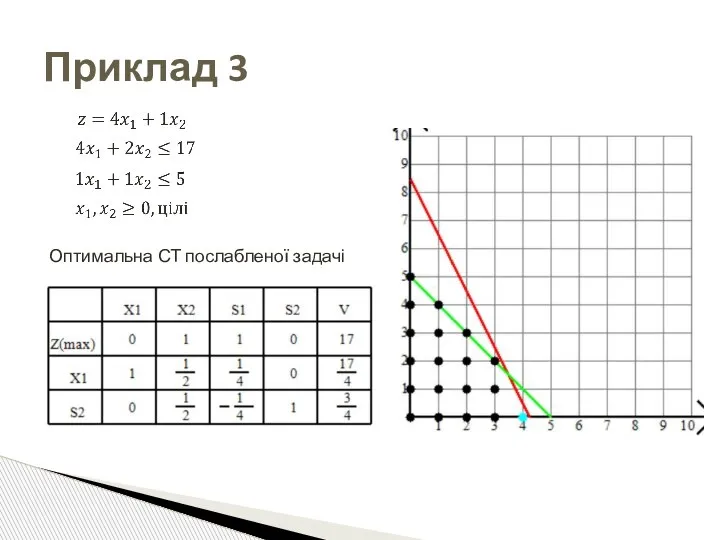
- 65. Приклад 3 Оптимальна СТ послабленої задачі
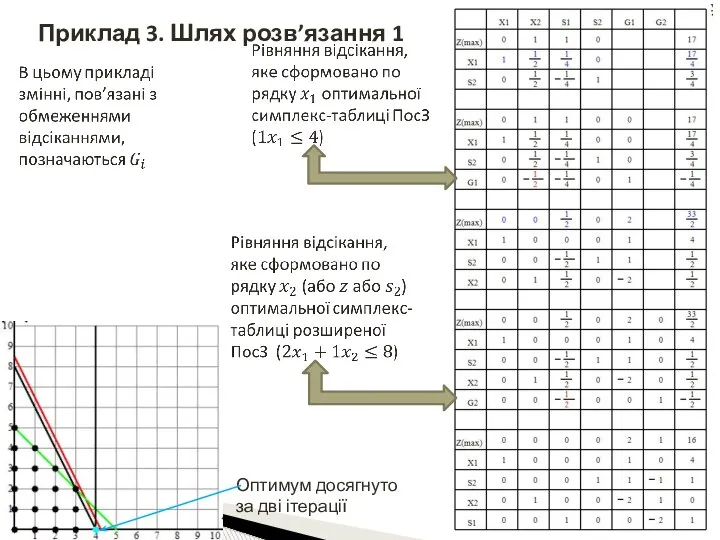
- 66. Приклад 3. Шлях розв’язання 1 Оптимум досягнуто за дві ітерації
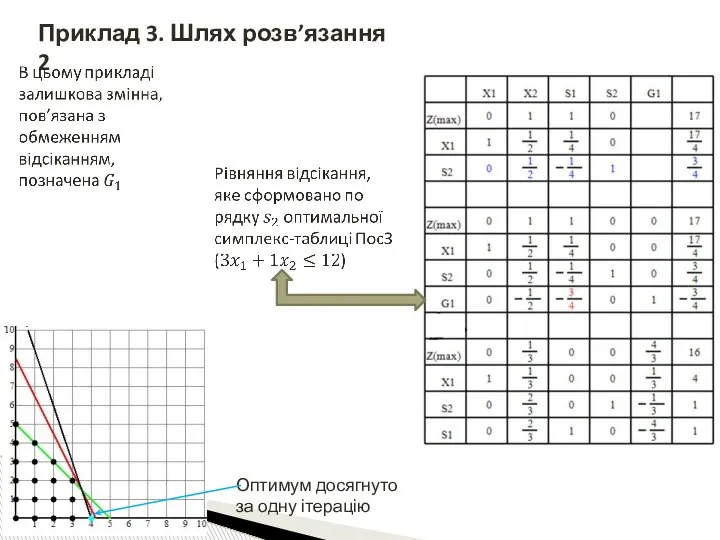
- 67. Приклад 3. Шлях розв’язання 2 Оптимум досягнуто за одну ітерацію
- 68. Ефективність відсікань Гоморі Одна і та ж оптимальна симплекс-таблиця розширеної ЗЛП породжує різні відсікання. ???? Яке
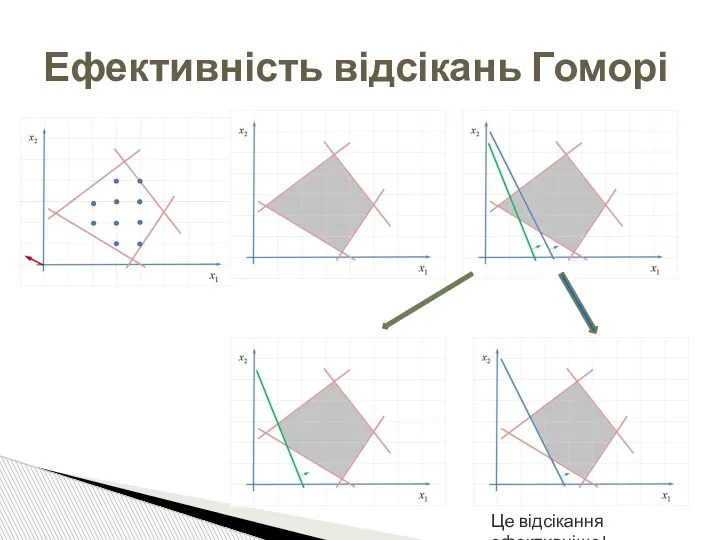
- 69. Ефективність відсікань Гоморі Це відсікання ефективніше!
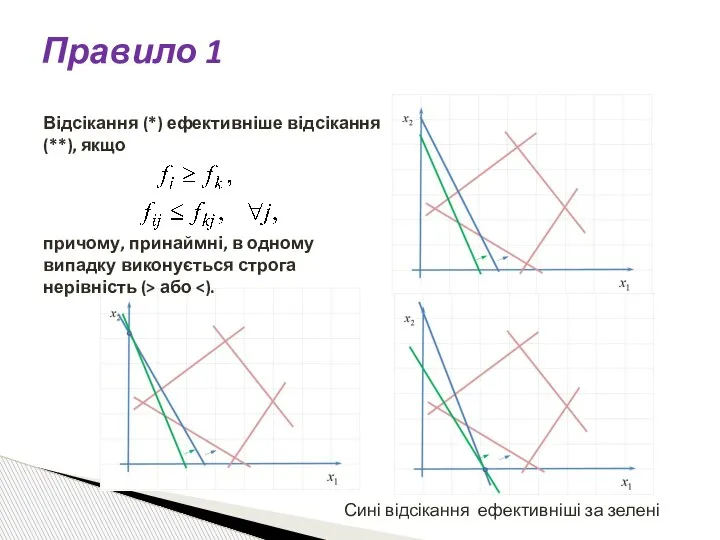
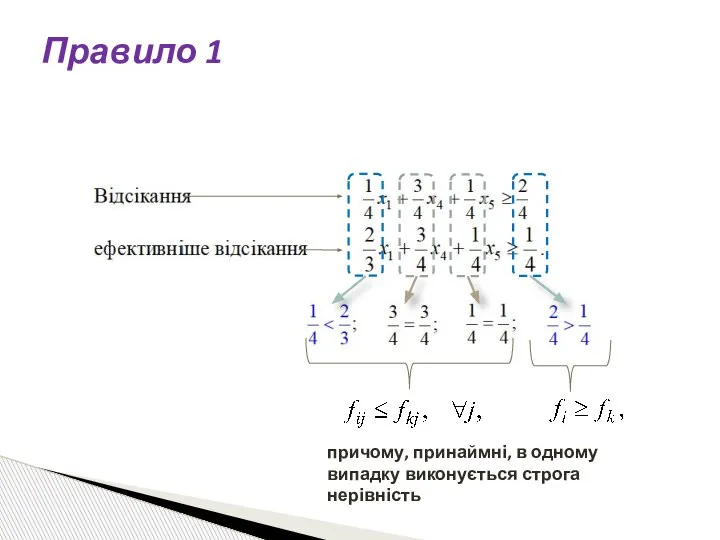
- 70. Правило 1. Відсікання (*) ефективніше відсікання (**), якщо причому, принаймні, в одному випадку виконується строга нерівність
- 71. Відсікання (*) ефективніше відсікання (**), якщо причому, принаймні, в одному випадку виконується строга нерівність (> або
- 72. Правило 1 причому, принаймні, в одному випадку виконується строга нерівність
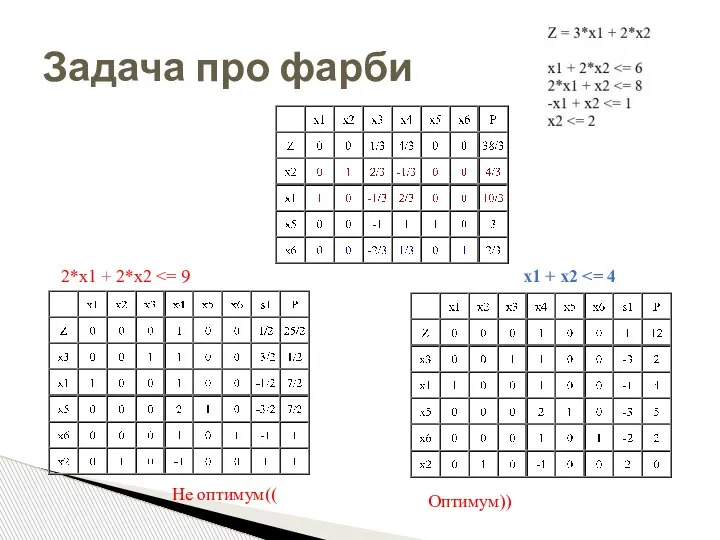
- 73. Задача про фарби 2*x1 + 2*x2 x1 + x2 Не оптимум(( Оптимум))
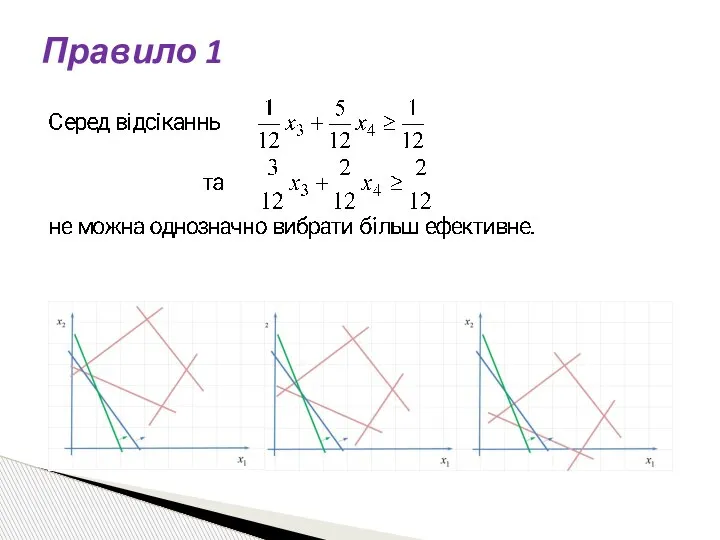
- 74. Правило 1
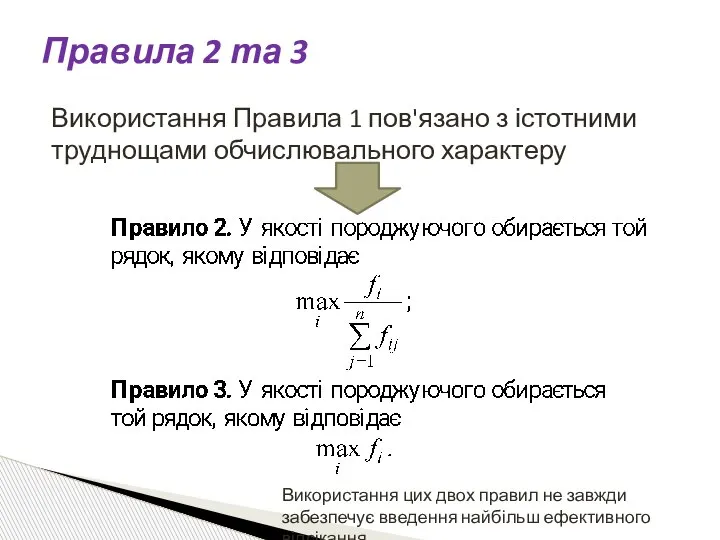
- 75. Використання Правила 1 пов'язано з істотними труднощами обчислювального характеру Використання цих двох правил не завжди забезпечує
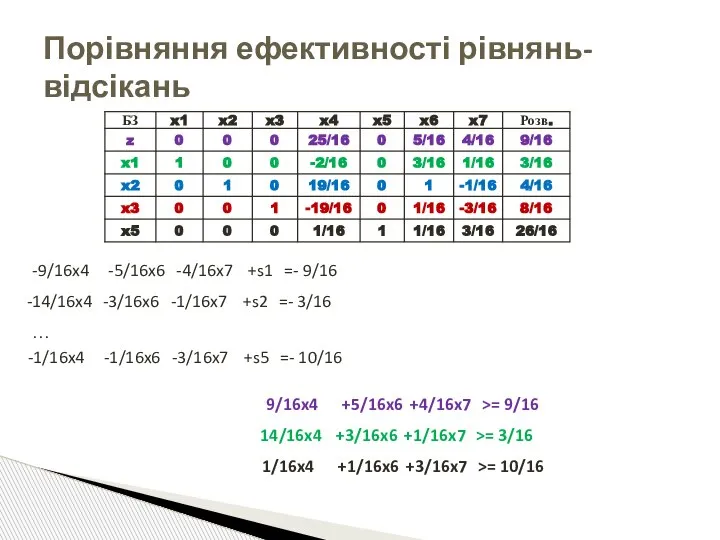
- 76. Порівняння ефективності рівнянь-відсікань -9/16x4 -5/16x6 -4/16x7 +s1 =- 9/16 -14/16x4 -3/16x6 -1/16x7 +s2 =- 3/16 -1/16x4
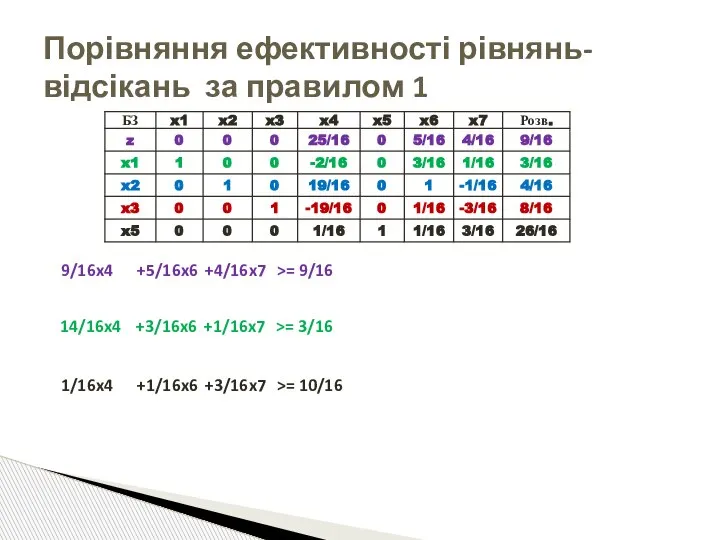
- 77. Порівняння ефективності рівнянь-відсікань за правилом 1 9/16x4 +5/16x6 +4/16x7 >= 9/16 14/16x4 +3/16x6 +1/16x7 >= 3/16
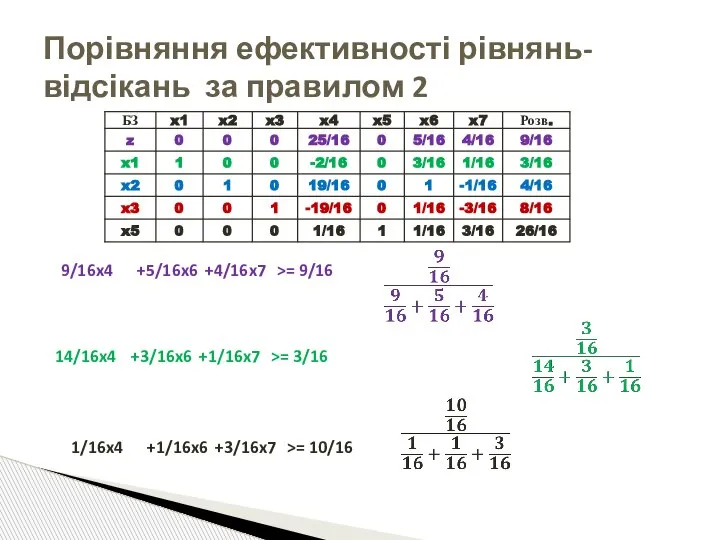
- 78. Порівняння ефективності рівнянь-відсікань за правилом 2 9/16x4 +5/16x6 +4/16x7 >= 9/16 14/16x4 +3/16x6 +1/16x7 >= 3/16
- 79. Порівняння ефективності рівнянь-відсікань за правилом 3 9/16x4 +5/16x6 +4/16x7 >= 9/16 14/16x4 +3/16x6 +1/16x7 >= 3/16
- 80. АГ знаходить розв’язок за скінчену кількість ітерацій
- 81. Помилки округлення, що виникають в процесі обчислень можуть привести до отримання невірного (не оптимального) цілочислового розв’язку
- 82. Приклад 3
- 83. Приклад 3
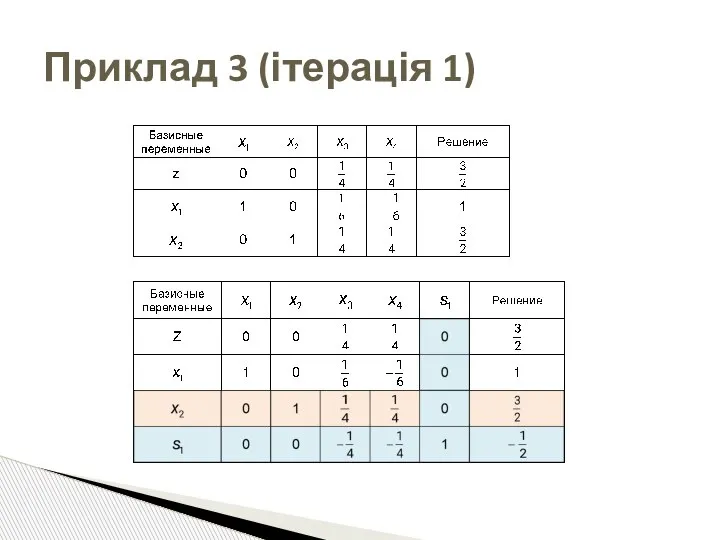
- 84. Приклад 3 (ітерація 1)
- 85. Приклад 3 (ітерація 1)
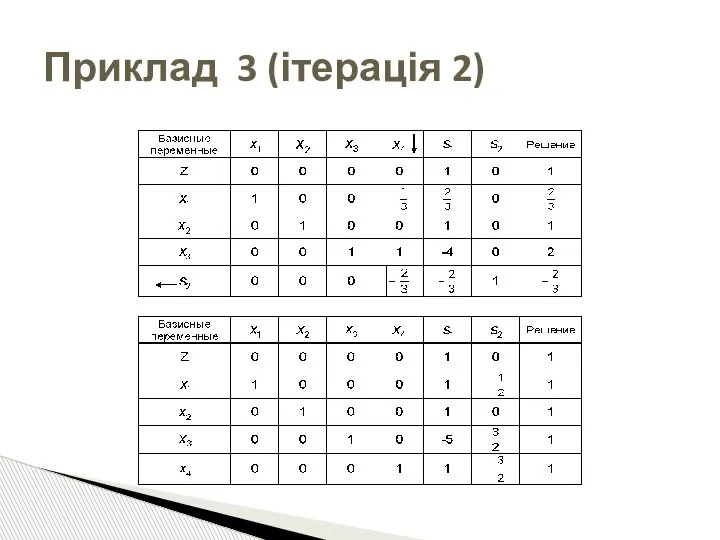
- 86. Приклад 3 (ітерація 2)
- 87. Приклад 3 (ітерація 2)
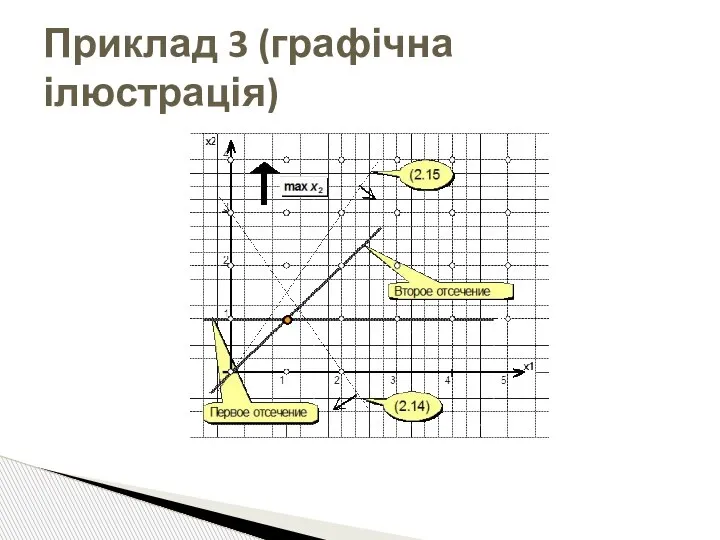
- 88. Приклад 3 (графічна ілюстрація)
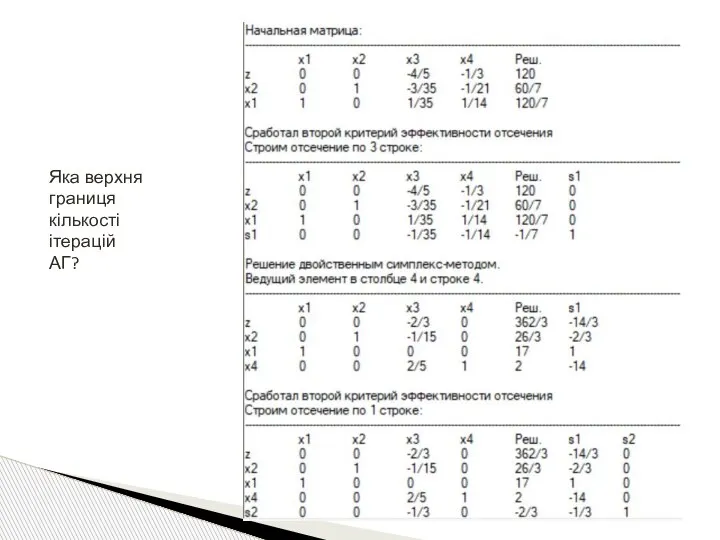
- 89. Яка верхня границя кількості ітерацій АГ?
- 91. Скачать презентацию



















![Виведення рівняння-відсікання Символом [α] позначатимемо цілу частину дійсного числа α: найбільше ціле,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1094724/slide-39.jpg)




















 Метод сложения
Метод сложения Классная работа по математике
Классная работа по математике Домашнее задание по теме операторы
Домашнее задание по теме операторы Статистические исследования на примере нашего класса
Статистические исследования на примере нашего класса Системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной Подобие треугольников. Решение задач по готовым чертежам. 8 класс
Подобие треугольников. Решение задач по готовым чертежам. 8 класс Лекция 8
Лекция 8 Виды треугольников
Виды треугольников Сложение и вычитание смешанных чисел. Подготовка к контрольной работе
Сложение и вычитание смешанных чисел. Подготовка к контрольной работе Алгоритмы нахождения независимого множества
Алгоритмы нахождения независимого множества Решение иррациональных уравнений
Решение иррациональных уравнений Презентация на тему Эллипс
Презентация на тему Эллипс  Очень жадный крокодил или больше, меньше, равно
Очень жадный крокодил или больше, меньше, равно Иррациональные неравенства. Неравенства с модулем
Иррациональные неравенства. Неравенства с модулем С математикой в космос
С математикой в космос Схемы изонити
Схемы изонити Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Презентация по математике "Названия чисел до двадцати" -
Презентация по математике "Названия чисел до двадцати" -  Портфоліо викладача математики та фізики Малишева Едуарда Миколайовича
Портфоліо викладача математики та фізики Малишева Едуарда Миколайовича Построение сечений многогранников
Построение сечений многогранников Правила деления. (6 класс)
Правила деления. (6 класс) Деление с остатком. Теоретическая часть
Деление с остатком. Теоретическая часть Интересные факты про математику
Интересные факты про математику Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15 Математический диктант
Математический диктант Как помочь ребенку понять математику. Вебинар 2
Как помочь ребенку понять математику. Вебинар 2 Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками
Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками