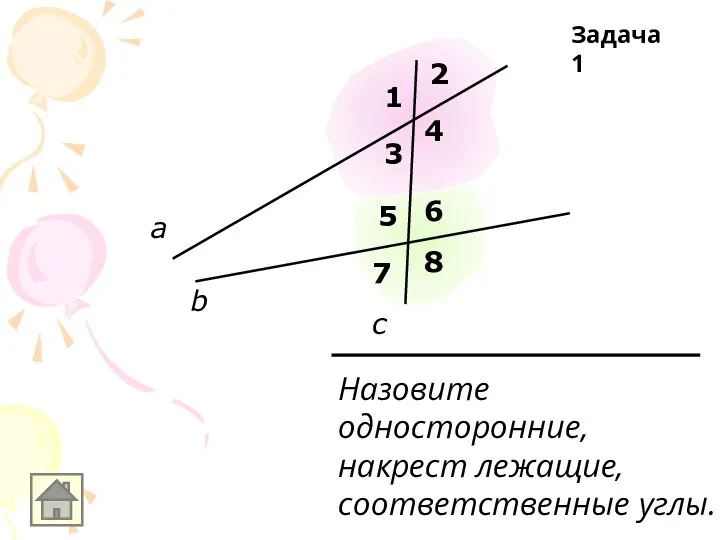
Слайд 2Назовите
односторонние,
накрест лежащие,
соответственные углы.
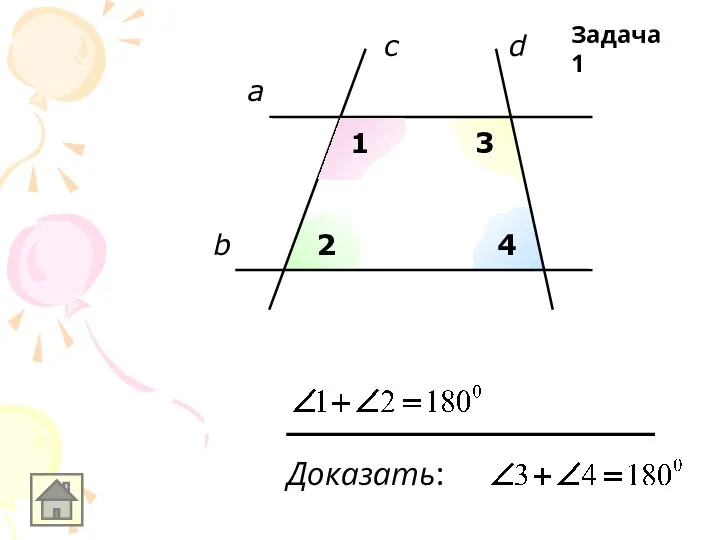
а
b
c
1
2
3
4
5
6
7
8
Задача 1
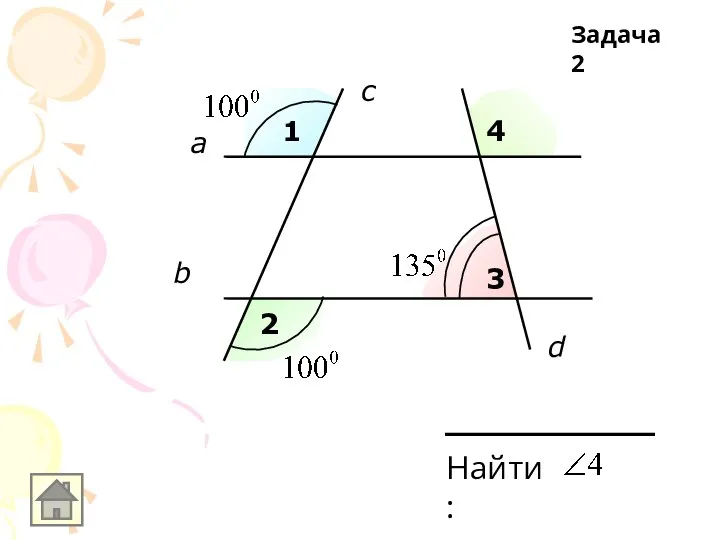
Слайд 3а
b
1
3
4
5
6
7
8
2
c
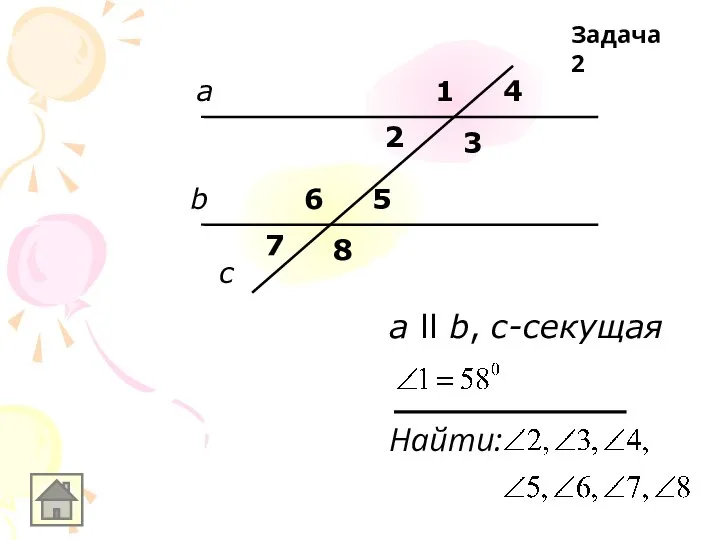
Найти:
а ll b, с-секущая
Задача 2
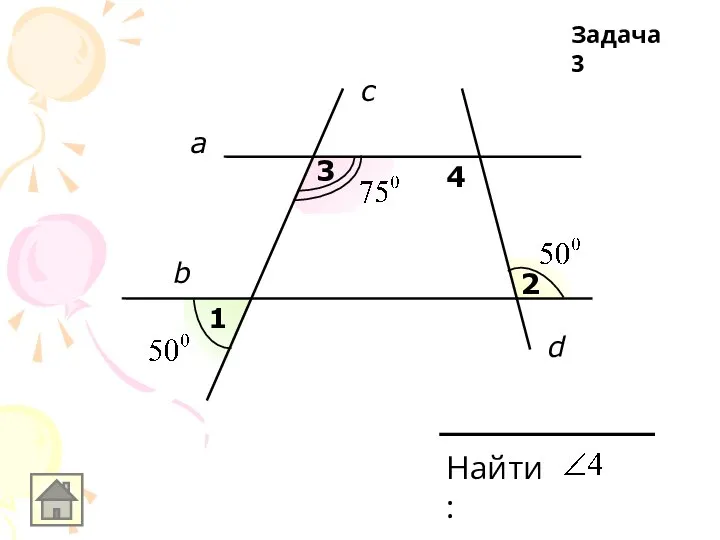
Слайд 41
2
а
b
c
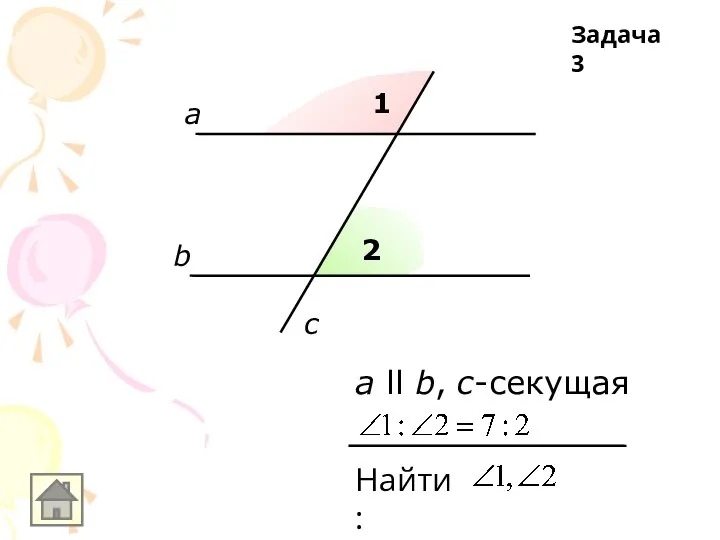
а ll b, с-секущая
Найти:
Задача 3
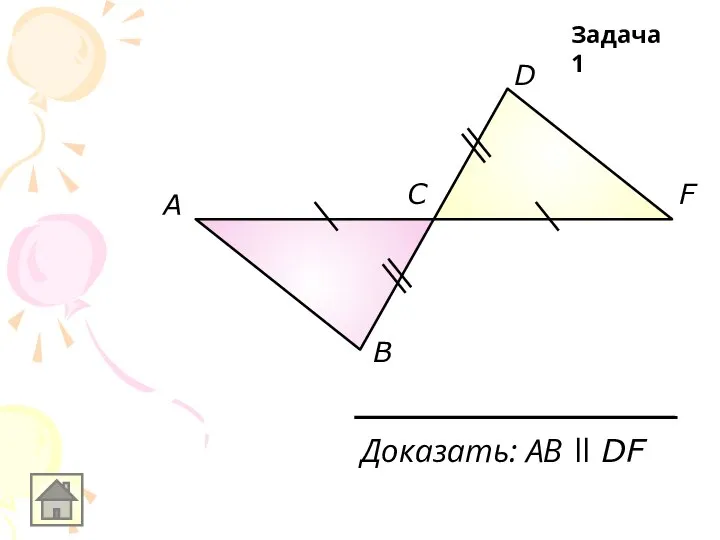
Слайд 6A
В
С
M
N
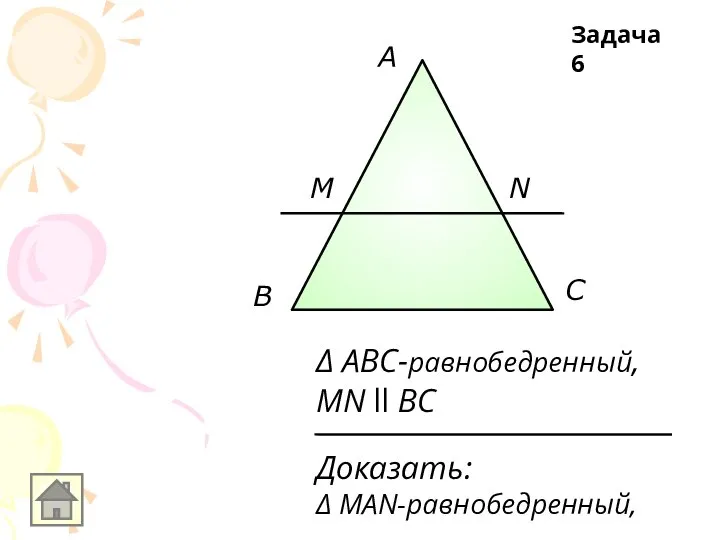
Доказать:
Δ MAN-равнобедренный,
Δ ABC-равнобедренный,
MN ll BC
Задача 6
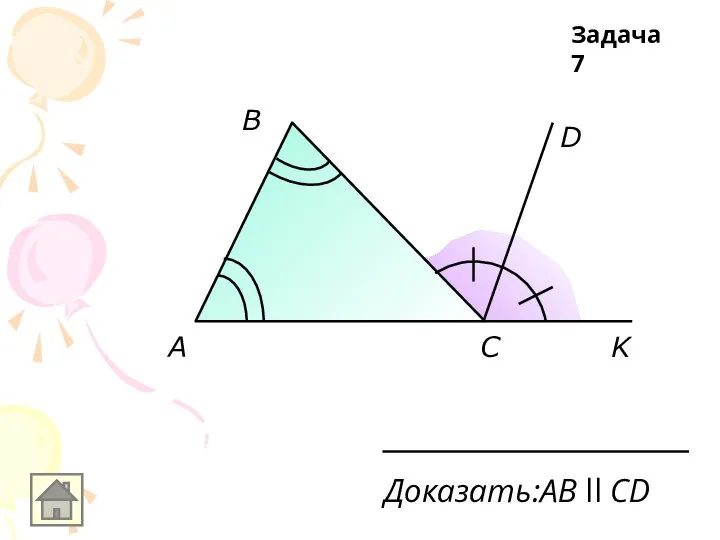
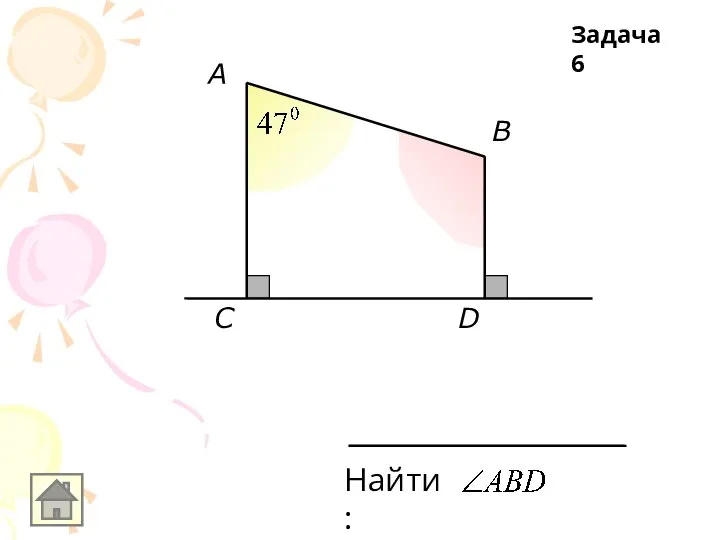
Слайд 7А
В
С
D
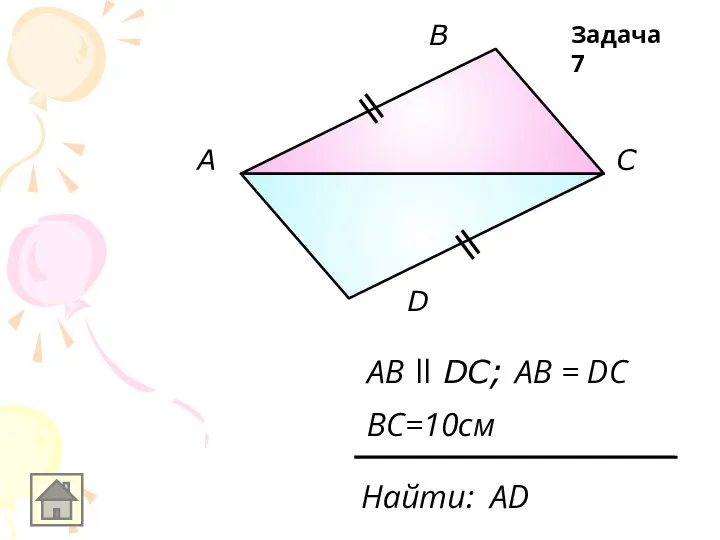
AB ll DC; AB = DC
Найти: АD
BC=10см
Задача 7
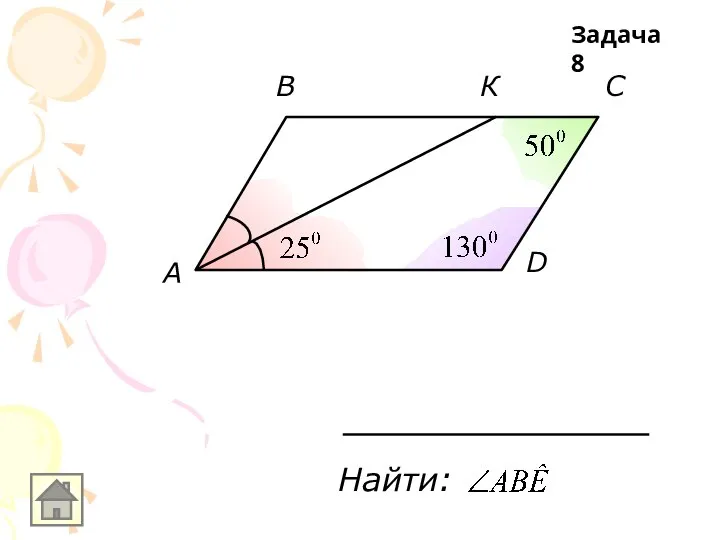
Слайд 8A
B
N
F
D
C
K
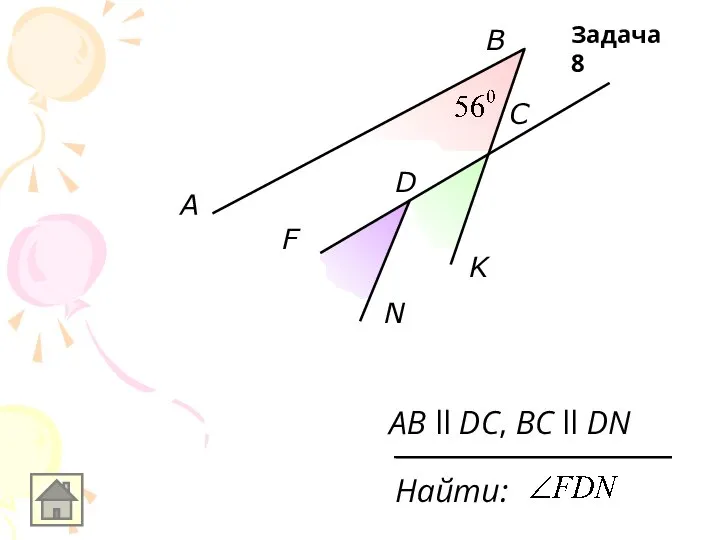
AB ll DC, BC ll DN
Найти:
Задача 8
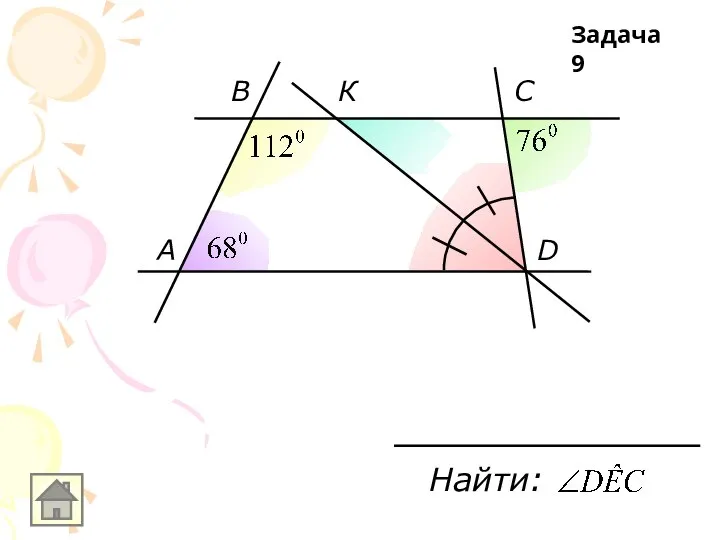
Слайд 9а
b
c
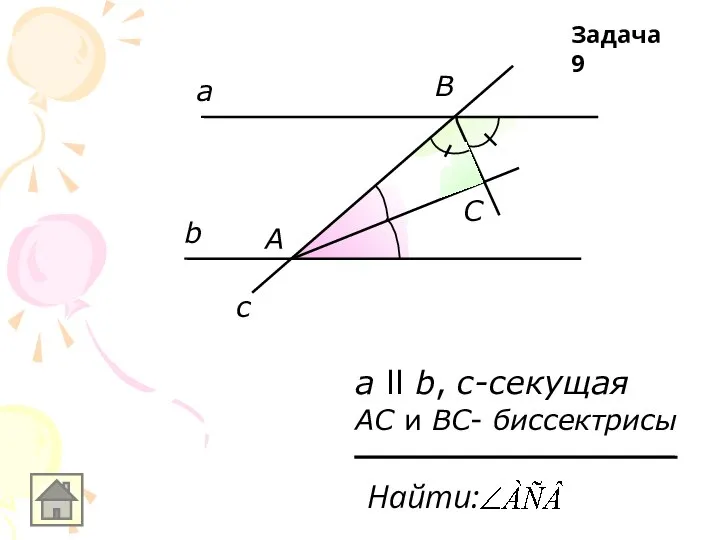
а ll b, с-секущая
А
В
С
АС и ВС- биссектрисы
Найти:
Задача 9
Слайд 10A
E
D
B
C
T
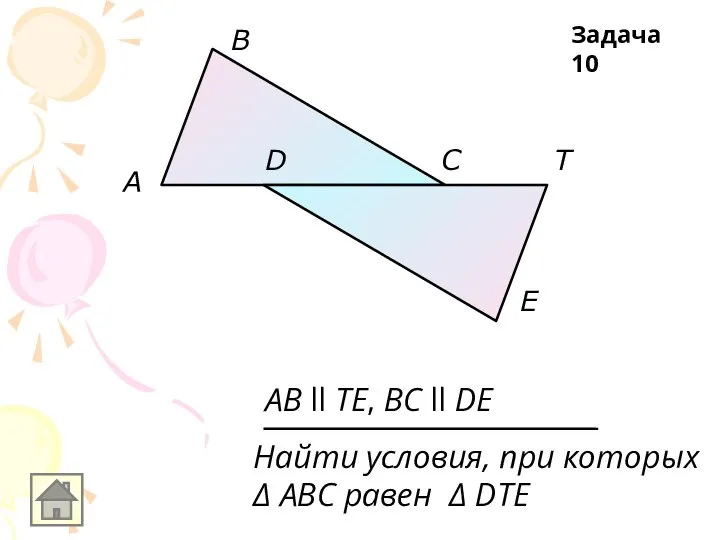
AB ll TE, BC ll DE
Найти условия, при которых
Δ АВС равен Δ
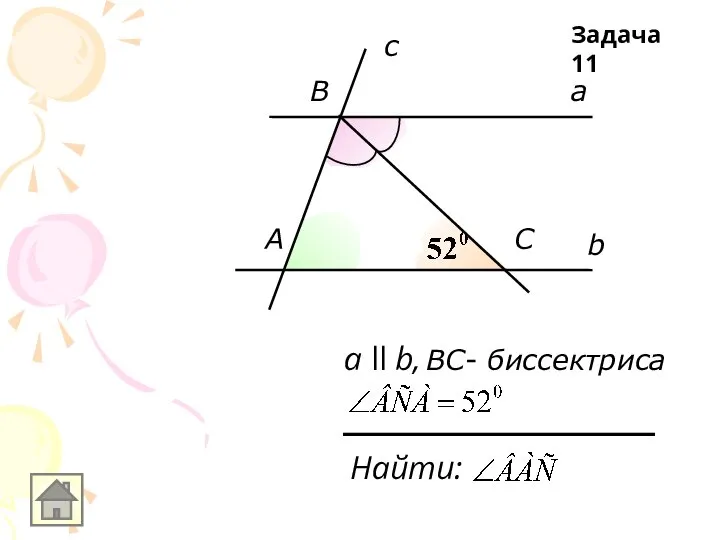
Слайд 11b
a
c
А
B
C
Найти:
а ll b, ВC- биссектриса
Задача 11
Слайд 12A
B
D
C
1
2
3
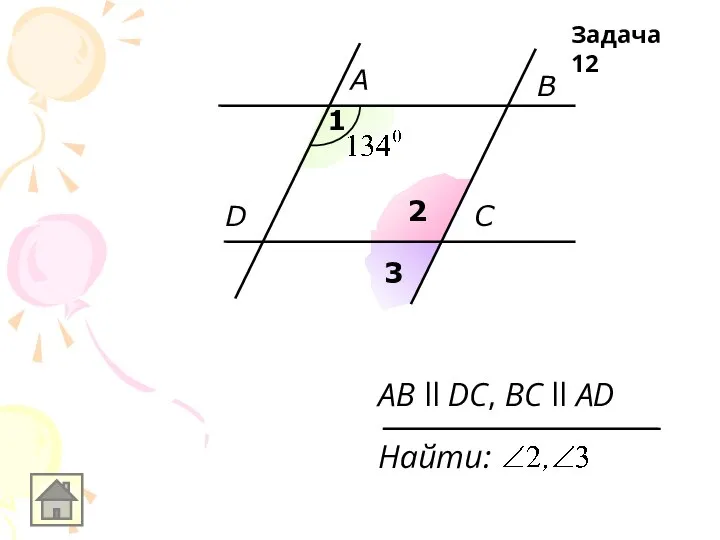
AB ll DC, BC ll AD
Найти:
Задача 12
Слайд 13А
В
С
M
N
O
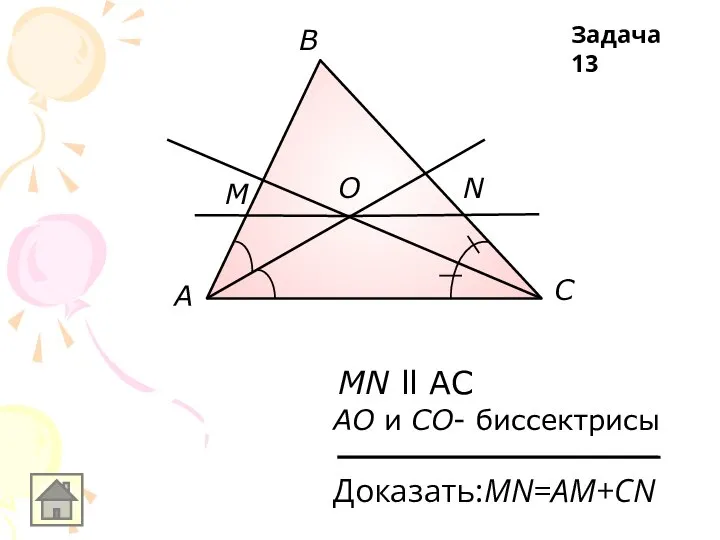
MN ll AC
АO и СO- биссектрисы
Доказать:MN=AM+CN
Задача 13
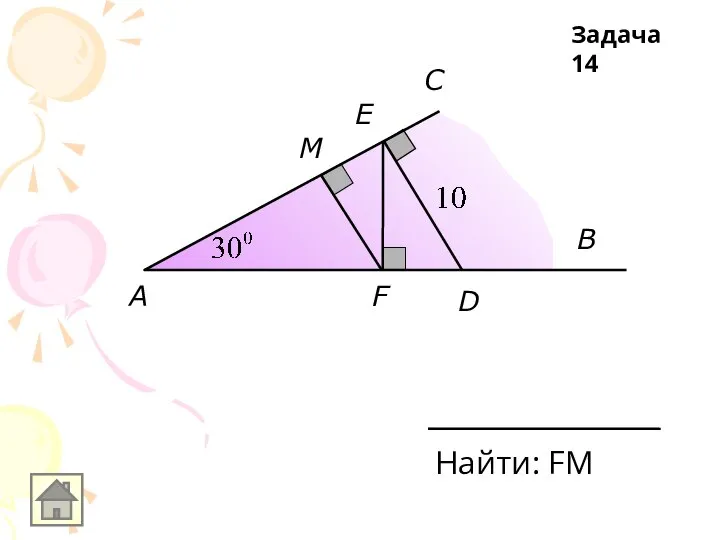
Слайд 14A
B
E
N
C
D
1
2
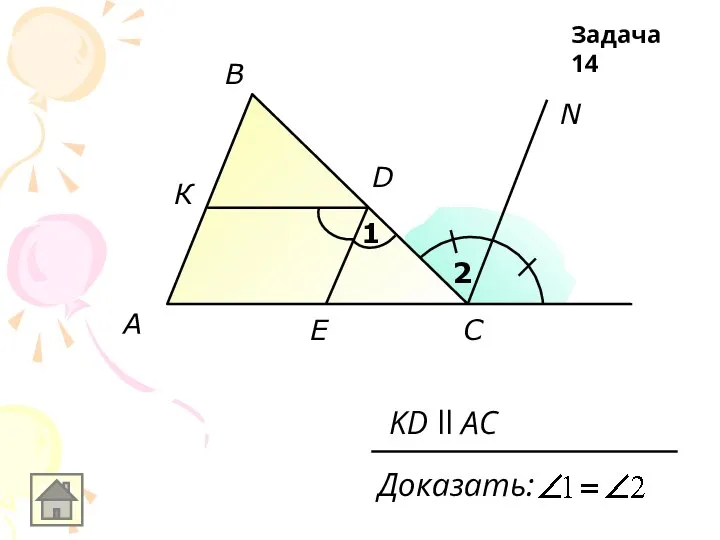
Доказать:
К
KD ll AC
Задача 14
Слайд 15A
D
C
B
1
2
3
4
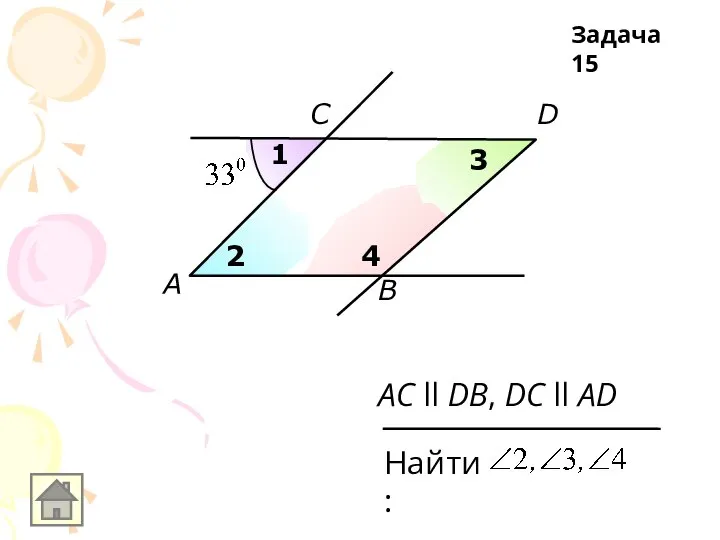
AC ll DB, DC ll AD
Найти:
Задача 15
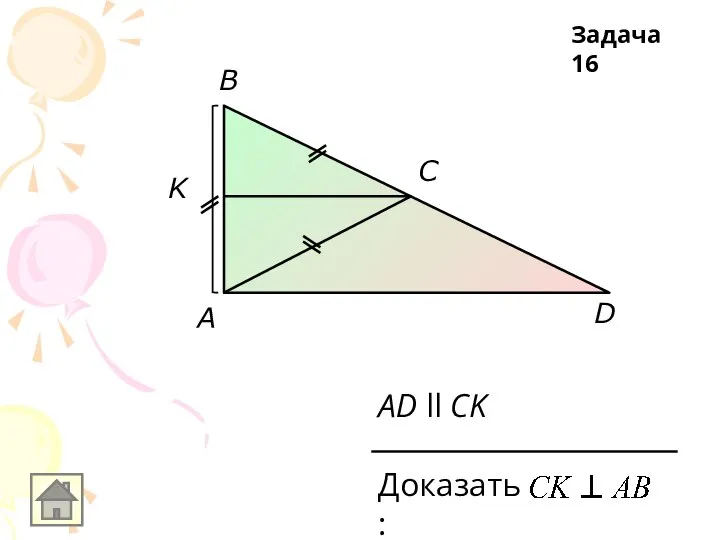
Слайд 17A
B
C
D
F
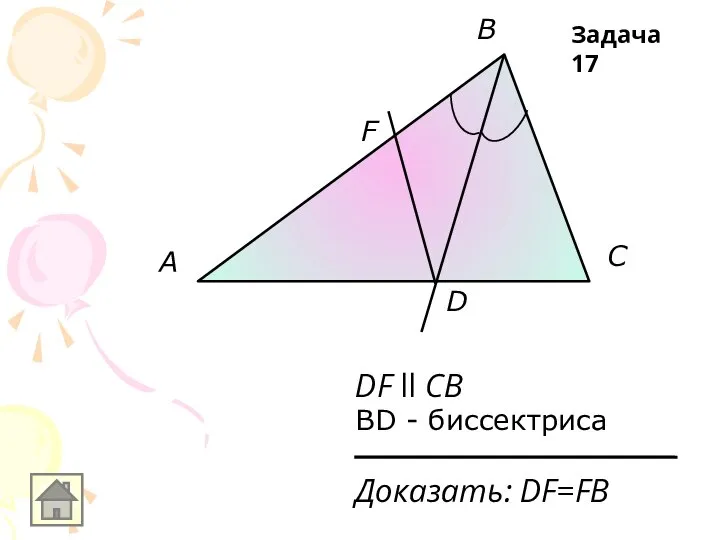
DF ll CB
BD - биссектриса
Доказать: DF=FB
Задача 17
Слайд 18A
B
C
D
E
F
M
K
AC ll DF,
DB ll EC
Доказать, что углы Δ АВМ
соответственно равны углам ΔEKF
Задача
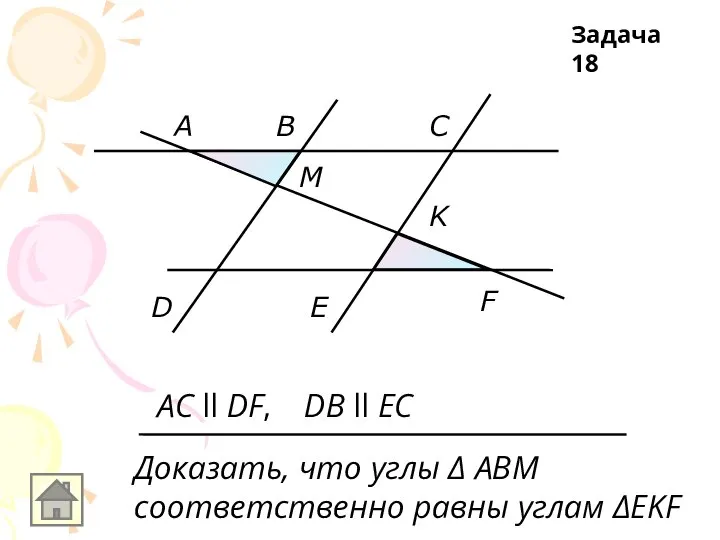
18
Слайд 19A
F
B
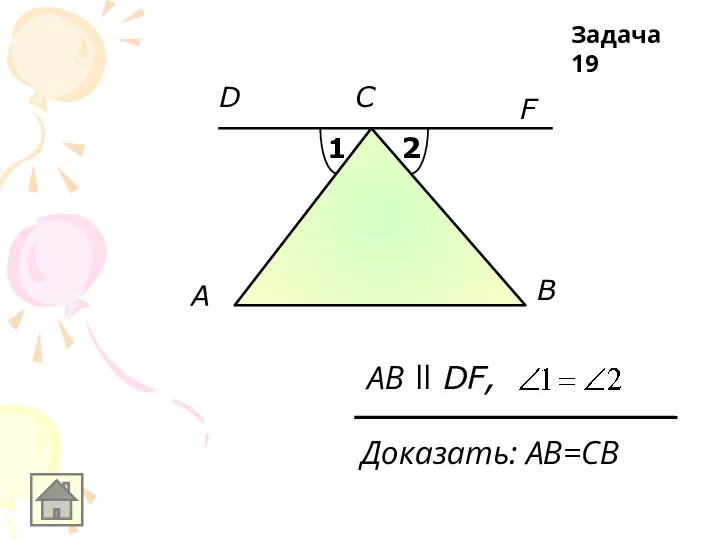
АB ll DF,
С
D
1
2
Доказать: АB=СВ
Задача 19
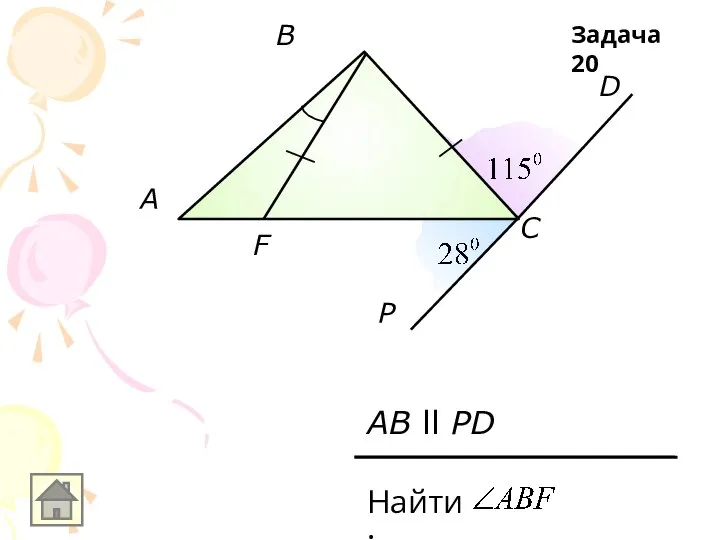
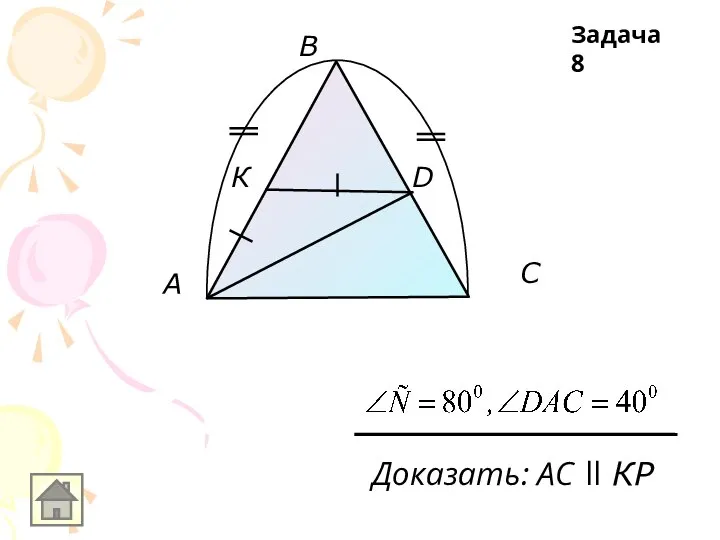
Слайд 21A
В
С
К
Р
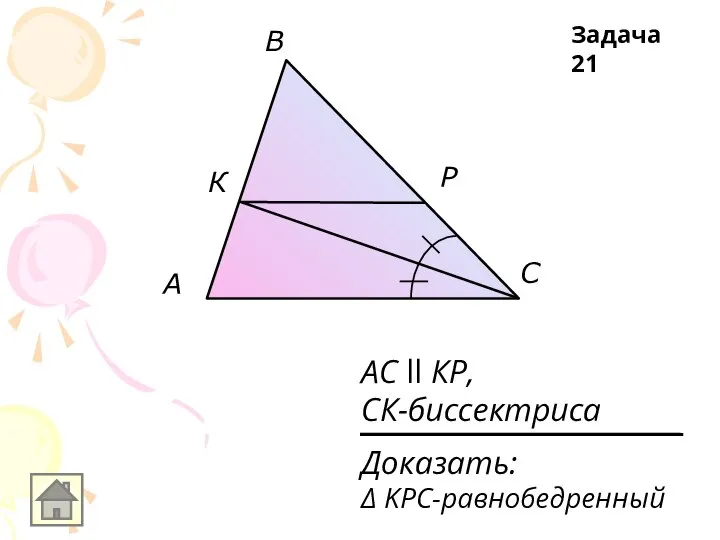
АС ll КР,
СК-биссектриса
Задача 21
Доказать:
Δ KPC-равнобедренный
Слайд 22O
A
D
B
C
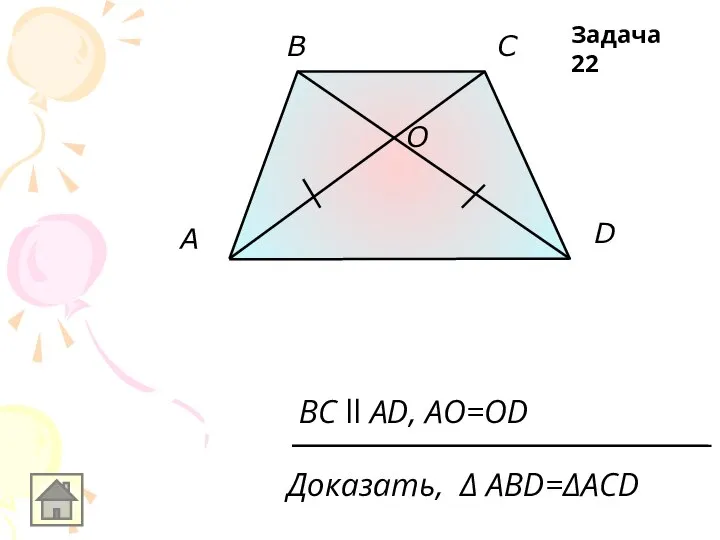
BC ll AD, AO=OD
Доказать, Δ АВD=ΔACD
Задача 22
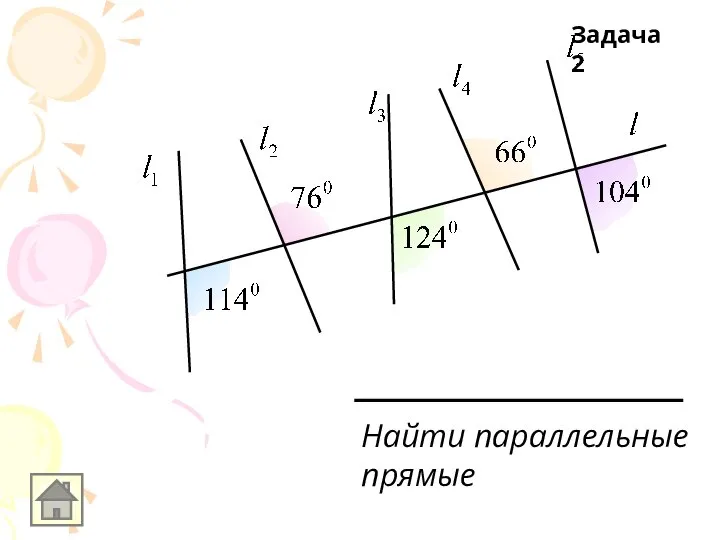
Слайд 26Найти параллельные
прямые
Задача 2
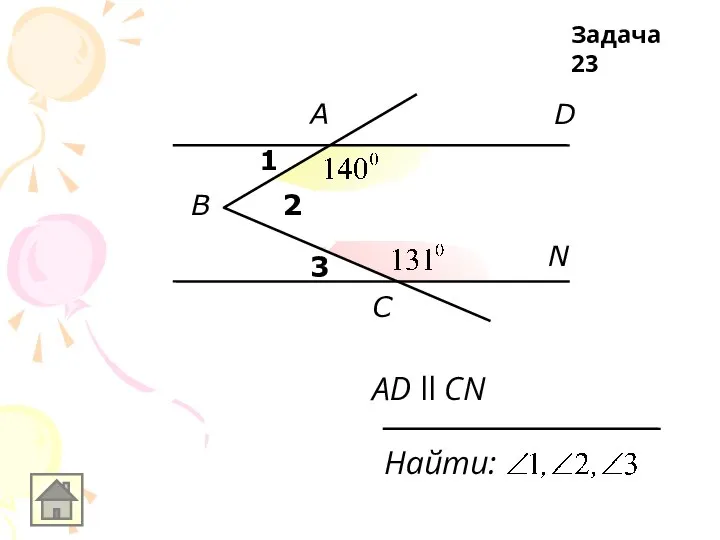
Слайд 27A
B
C
D
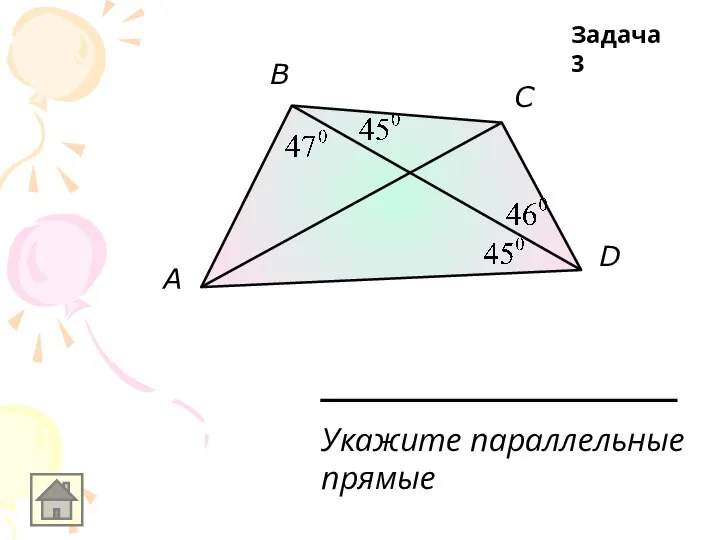
Укажите параллельные
прямые
Задача 3
Слайд 28A
A1
В
С
В1
С1
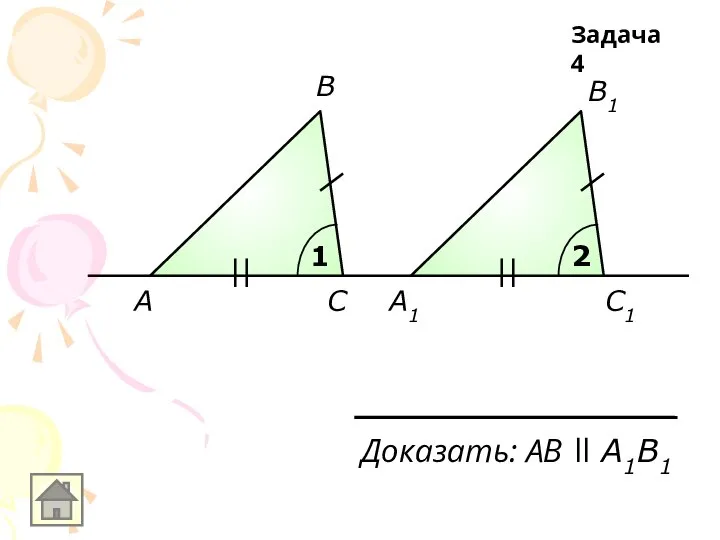
1
2
Доказать: АB ll A1B1
Задача 4
Слайд 30A
C
D
F
B
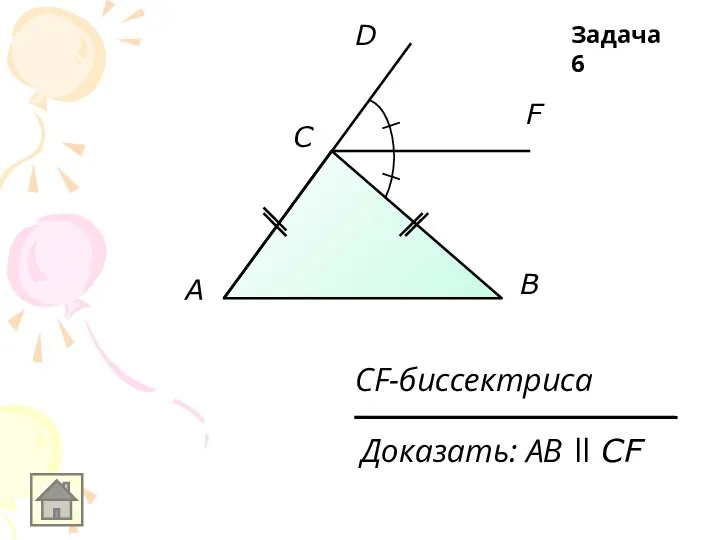
Доказать: АB ll CF
CF-биссектриса
Задача 6
Слайд 33A
B
E
C
D
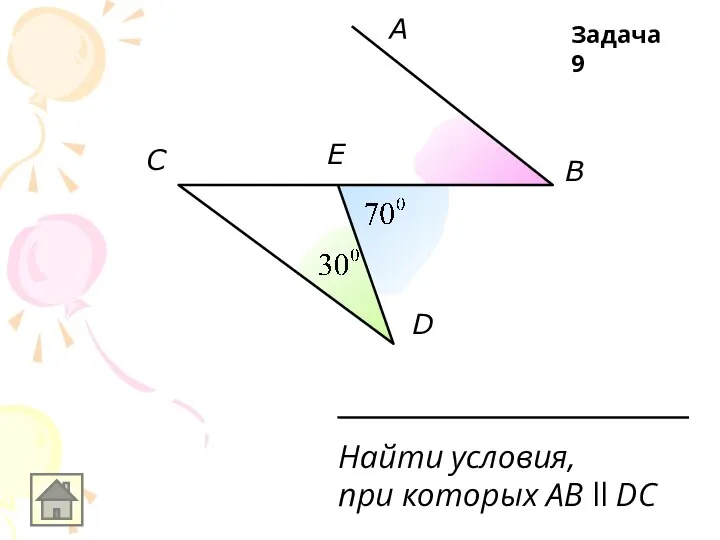
Найти условия,
при которых AB ll DC
Задача 9
Слайд 34A
D
C
B
F
M
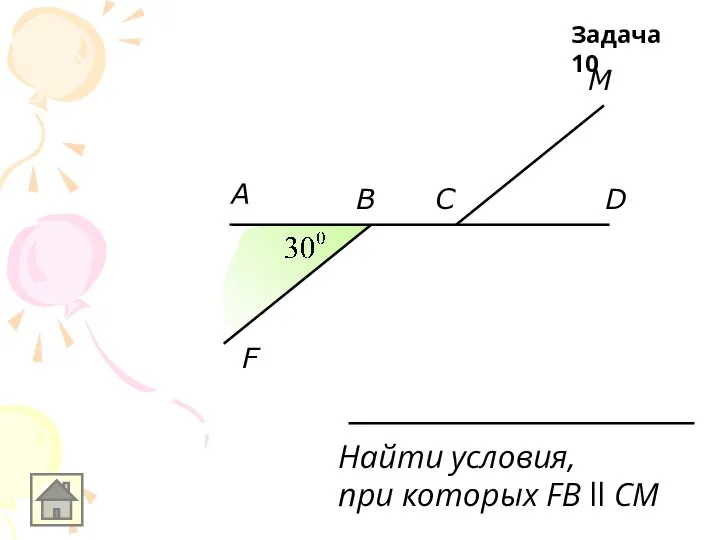
Найти условия,
при которых FB ll CM
Задача 10
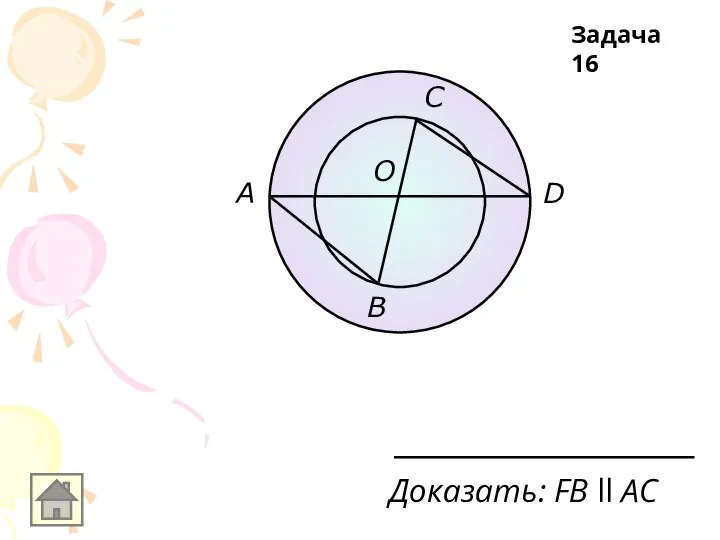
Слайд 35A
D
F
C
B
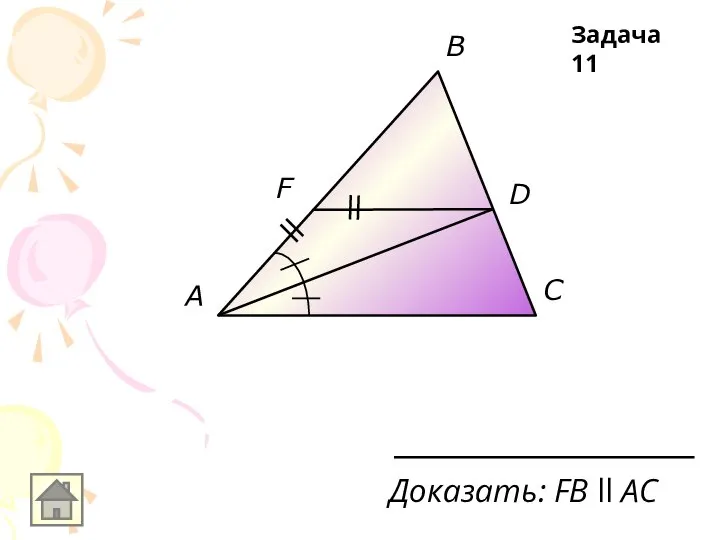
Доказать: FВ ll АС
Задача 11
Слайд 36A
В
О
С
D
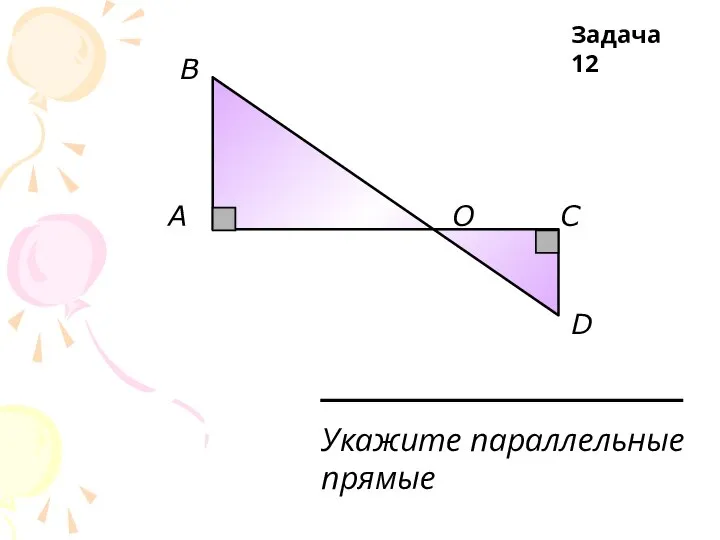
Укажите параллельные
прямые
Задача 12
Слайд 37A
B
C
D
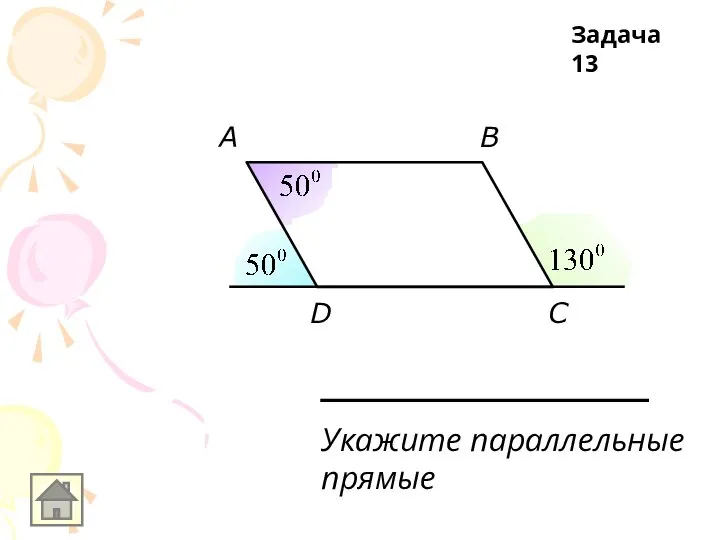
Укажите параллельные
прямые
Задача 13
Слайд 39B
A
О
D
С
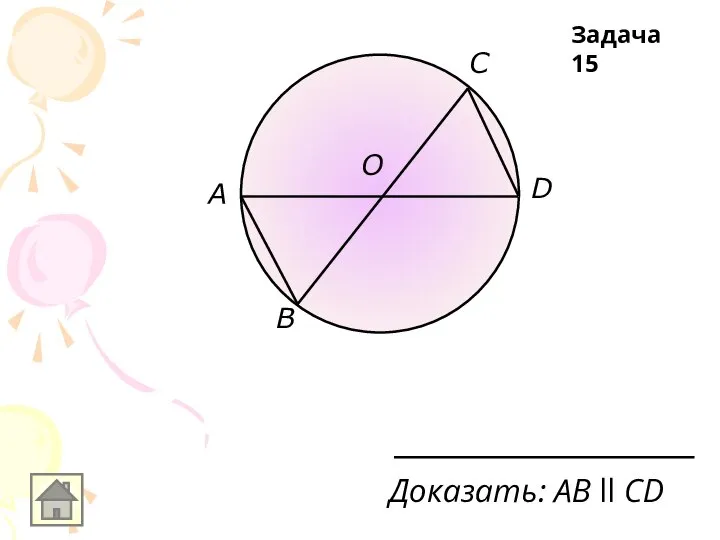
Доказать: AВ ll CD
Задача 15
Слайд 45а ll b, с-секущая
АС и ВD- биссектрисы
Доказать: АС ll ВD
Задача 4
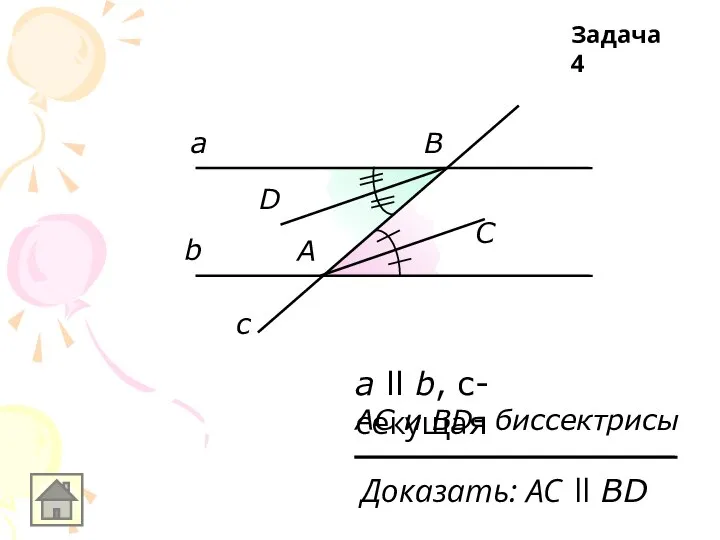
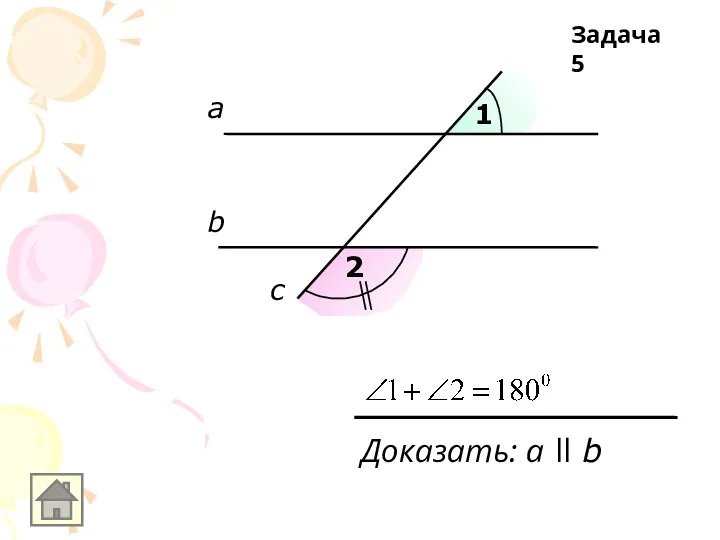
Слайд 46а
b
c
а ll b, с-секущая
АС и ВD- биссектрисы
А
С
В
D
Доказать: АС ll ВD
Задача 5
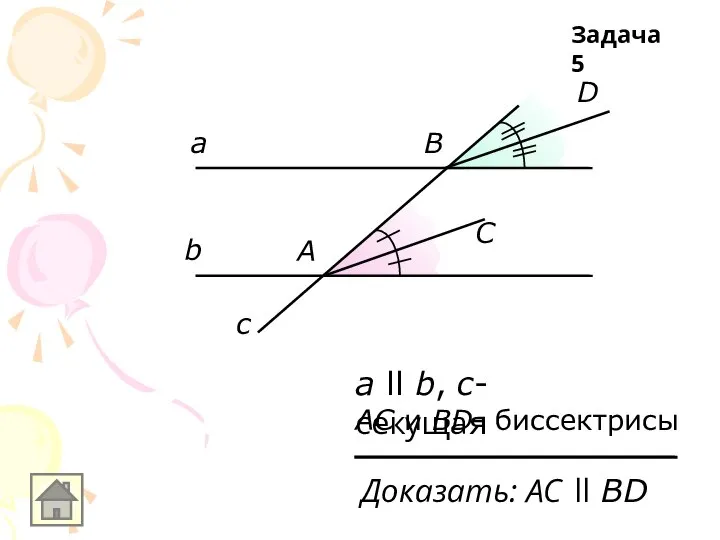
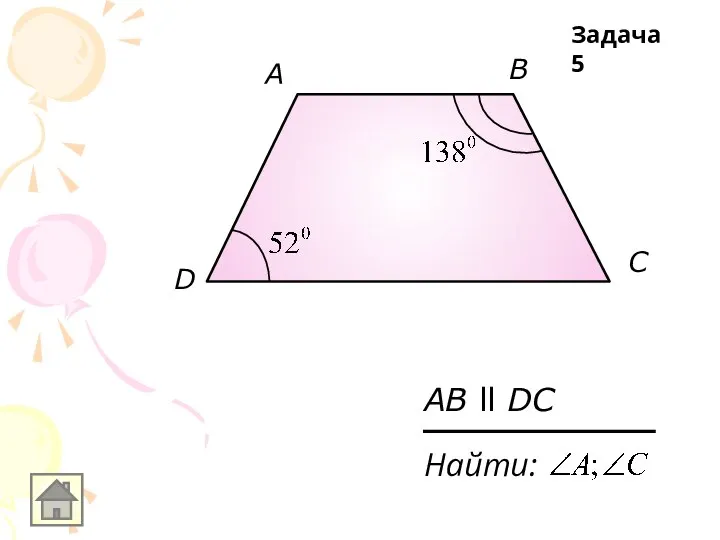
Слайд 48С
В
К
A
D
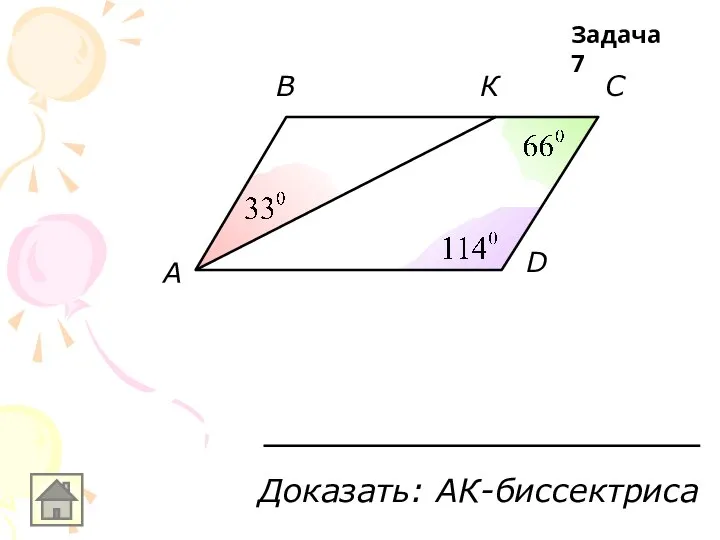
Доказать: АК-биссектриса
Задача 7

































 Производная функции
Производная функции Упрощение выражений. Решение задач
Упрощение выражений. Решение задач Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности
Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности Математический кроссворд
Математический кроссворд Метрологическое обеспечение на базе профессионального стандарта Специалист по метрологии
Метрологическое обеспечение на базе профессионального стандарта Специалист по метрологии Схемы к задачам
Схемы к задачам Теория процентов
Теория процентов Приведение дробей к общему знаменателю,
Приведение дробей к общему знаменателю, Подготовка к контрольной работе
Подготовка к контрольной работе Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса
Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса Умники и умницы. Викторина по математике
Умники и умницы. Викторина по математике Основное логарифмическое тождество
Основное логарифмическое тождество Презентация 1
Презентация 1 Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Степень с отрицательным показателем
Степень с отрицательным показателем Числовые ряды
Числовые ряды Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Задача по математике (1 класс)
Задача по математике (1 класс) Производная функции
Производная функции Развертка, площадь боковой и полной поверхности пирамиды и усеченной пирамиды
Развертка, площадь боковой и полной поверхности пирамиды и усеченной пирамиды Параллельные прямые
Параллельные прямые График функции. Тест
График функции. Тест Бинарный урок физики и геометрии
Бинарный урок физики и геометрии Производная в заданиях уровня В. ЕГЭ
Производная в заданиях уровня В. ЕГЭ Кривые, заданные параметрически
Кривые, заданные параметрически Корреляция. Показатель корреляции
Корреляция. Показатель корреляции Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Устные упражнения. Площади различных фигур
Устные упражнения. Площади различных фигур