Застосування кількох способів розкладання многочленів на множники

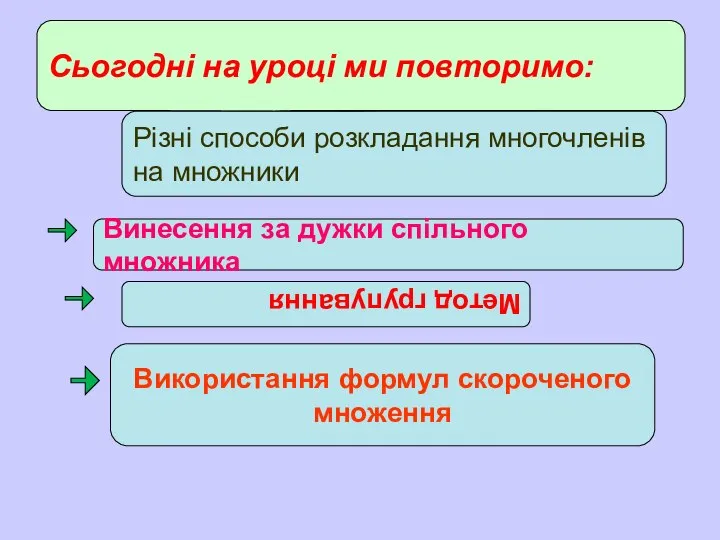
Сьогодні на уроці ми повторимо:
Різні способи розкладання многочленів
на множники
Винесення за дужки спільного множника
Метод групування
Використання формул скороченого
множення

Щоб розкласти многочлен на множники, винесенням спільного множника за дужки, потрібно:
1. Знайти цей спільний множник;
2. Винести його за дужки.

Алгоритм розкладання многочлена на множники винесенням за дужки спільного множника
Знаходимо спільний числовий множник для коефіцієнтів (якщо цілі числа, то шукаємо НСД );
2. Виносимо за дужки змінну з меншим показником;
12а3b + 8а2b2 =
НСД(12;8) = 4
= 4а2b (3а + 2b)

Алгоритм розкладання многочленів на множники способом групування
Розбити всі члени многочлена на групи так, щоб після винесення за дужки спільного множника в такій групі в дужках утворилися спільні множники;
Винести за дужки спільний множник у кожній групі;
Винести за дужки спільний двочленний множник.
= (ах + ау) + (5х + 5у) =
= а(х + у ) + 5(х + у) =
= (х + у)(а + 5)
ax + ay + 5x + 5y =

Запиши в зошит
3х + 3у – bх – bу
(3х +3у) – (bх + bу)
3(х + у) – b(х + у)
(х + у)(3 – b)

1. Якщо маємо двочлен, то доречно перевірити, чи не можливо використати формулу різниці квадратів або ж формулу різницю (суму) кубів ;
2. Якщо маємо тричлен, то перевірити, чи не можливо його перетворити на квадрат двочлена.
Щоб розкласти многочлен на множники, використовуючи формули скороченого множення, потрібно:

Пригадай
ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ
РІЗНИЦЯ КВАДРАТІВ
a2-b2=(а –b)(а + b)

ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ
КВАДРАТ СУМИ ДВОХ ЧИСЕЛ
( а + b)2 = а2 + 2аb + b2
КВАДРАТ РІЗНИЦІ ДВОХ ЧИСЕЛ
(а - b)2 = а2 - 2аb + b2

ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ
Cума кубів
a3+b3=(a+b)(a2-ab+b2)
Різниця кубів
a3-b3=(a-b)(a2+ab+b2)

Знайди умову і відповідь
запиши в зошит
Завдання
a2-64
4xy-2x2
(3a+3x)+(ya+xy)
x2+4x+4
a3+27
3a4x+9a3x2-27a2x3
Відповіді
а) (x+2)(x+2)
б) 3a2x(a2+3ax-9x2)
в) (3+y)(a+x)
г) (a+8)(a-8)
д) (a+3)(a2-3a+9)
е) 2x(2y-x)
1г, 2е, 3в, 4а, 5д, 6б

Гра “Знайди помилку”
Запиши в зошит і виправ помилку

Перевір себе

Щоб розкласти многочлен на множники, використовуючи одночасно декілька методів
ТРЕБА:
Якщо можливо винести за дужки спільний множник, виконайте це.
Поглянь, чи не можливо використати
формули: різницю квадратів або
різницю (суму) кубів.
Якщо не вдається застосувати формули
скороченого множення, то спробуйте
скористатись методом групування.
Коли ви закінчили розклад на множники,
корисно перевірити за допомогою множення,
чи вірний отриманий вами результат.

Пошук способів розкладання многочлена на множники
4a3-ab2
Запиши в зошит з розв’язанням
1. Винести спільний множник, якщо він є, за дужки
4a3-ab2 =a(4a2-b2)
2. Застосувати формулу скороченого множення (якщо це можливо)
a(4a2-b2)=a(2a-b)(2a+b)
3. Застосувати спосіб групування, якщо попередні
не дали результату
x2+2x+1-a2= (x2+2x+1)-a2=(x+1)2-a2=(x+1+a) (x+1-a)

Прислів’я
Життя –
це море,
пливти
бажаєш -
Будуй
човен
із добрих
справ.

Підсумок уроку
Продовжіть речення:
Розкладання многочлена на множники розпочинаю з …
Якщо задано тричлен то спробую
застосувати…
Якщо добуток дорівнює
нулю то…

Домашнє завдання:
Підручник §19
№790, №793,
№827, №828