Содержание
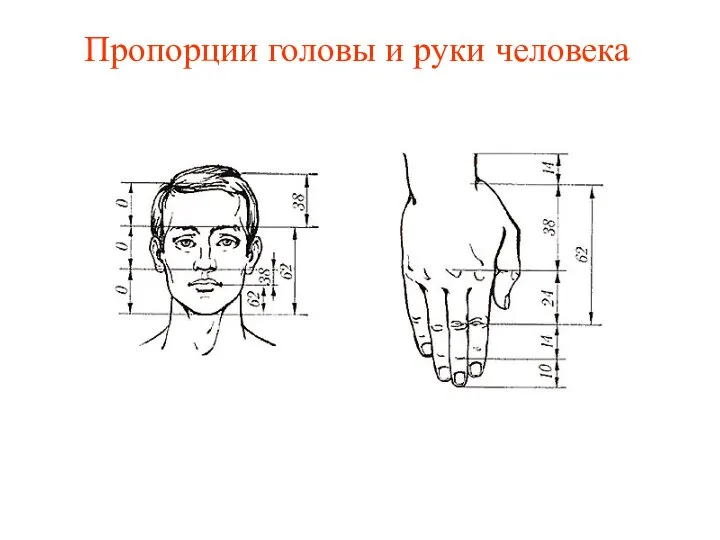
- 2. Пропорции головы и руки человека
- 3. Парфенон Одно из красивейших произведений древнегреческой архитектуры - Парфенон в Афинах (V в.до н.э.) содержит в
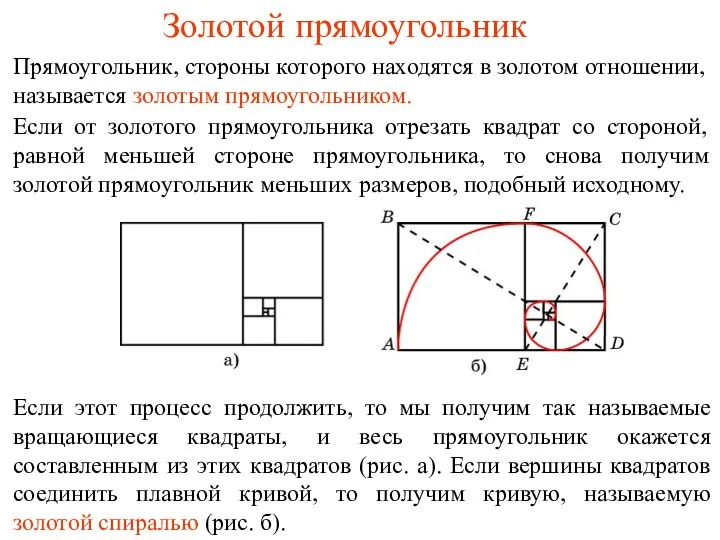
- 4. Золотой прямоугольник Прямоугольник, стороны которого находятся в золотом отношении, называется золотым прямоугольником. Если от золотого прямоугольника
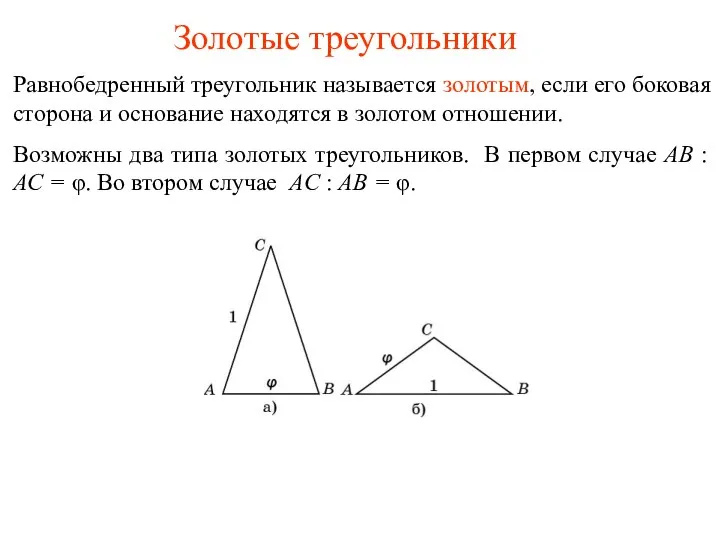
- 5. Золотые треугольники Равнобедренный треугольник называется золотым, если его боковая сторона и основание находятся в золотом отношении.
- 6. Золотые треугольники Теорема. Золотыми треугольниками являются равнобедренные треугольники с углами при вершинах 36о и 108о. Доказательство.
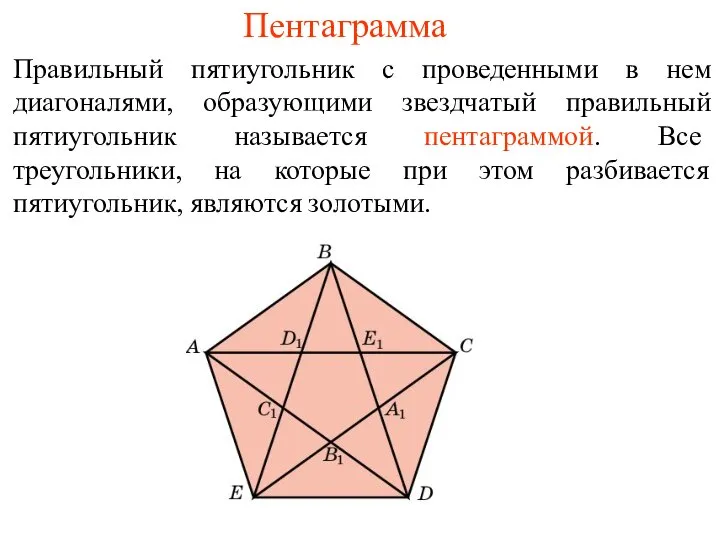
- 7. Пентаграмма Правильный пятиугольник с проведенными в нем диагоналями, образующими звездчатый правильный пятиугольник называется пентаграммой. Все треугольники,
- 8. Вопрос 1 Что называется золотым сечением? Ответ: Золотым сечением называется такое делением целого на две неравные
- 9. Вопрос 2 Каким числом выражается золотое сечение?
- 10. Вопрос 3 Как обозначается число, выражающее золотое сечение? Ответ: φ.
- 11. Вопрос 4 В честь кого золотое сечение обозначается буквой φ? Ответ: В честь древнегреческого скульптора Фидия.
- 12. Вопрос 5 Какой прямоугольник называется золотым? Ответ: Золотым прямоугольником называется прямоугольник, стороны которого находятся в золотом
- 13. Вопрос 6 Какие треугольники называются золотыми? Ответ: Золотым называется равнобедренный треугольник, боковая сторона и основание которого
- 14. Вопрос 7 Что такое пентаграмма? Ответ: Пентаграммой называется правильный пятиугольник с проведенными в нем диагоналями.
- 15. Упражнение 1 На рисунке окружность с центром в точке О касается прямой АВ в точке В,
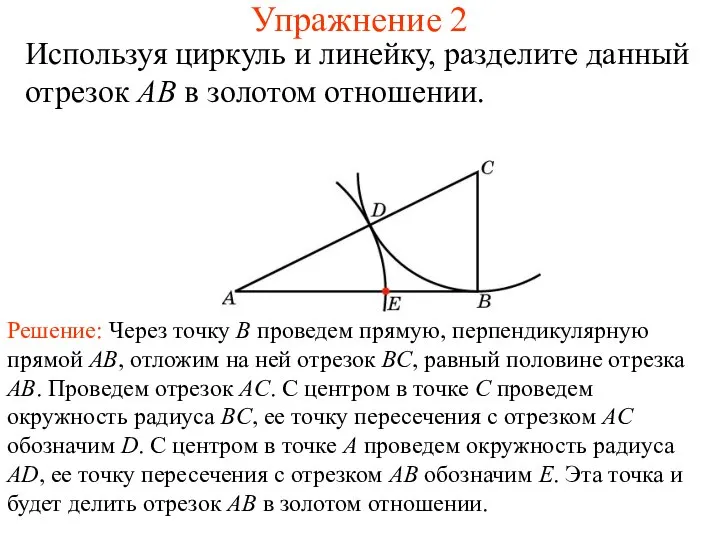
- 16. Упражнение 2 Используя циркуль и линейку, разделите данный отрезок AB в золотом отношении.
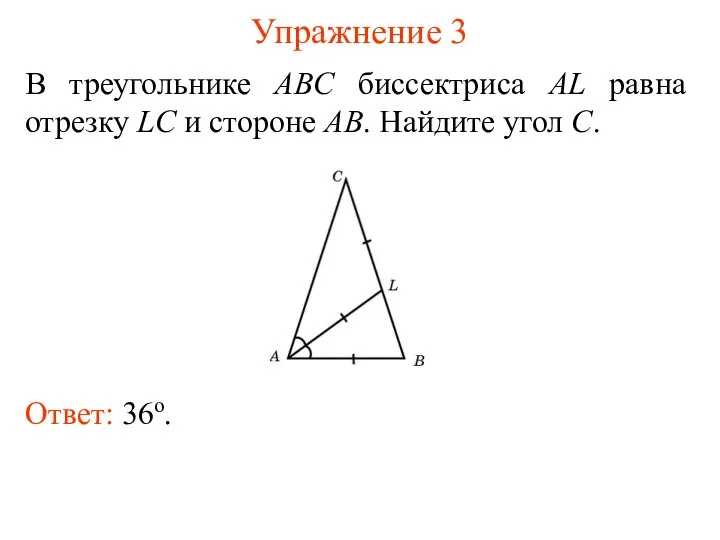
- 17. Упражнение 3 В треугольнике ABC биссектриса AL равна отрезку LC и стороне AB. Найдите угол C.
- 18. Упражнение 4 Биссектриса, проведенная из вершины основания равнобедренного треугольника, равна основанию. Найдите угол при основании этого
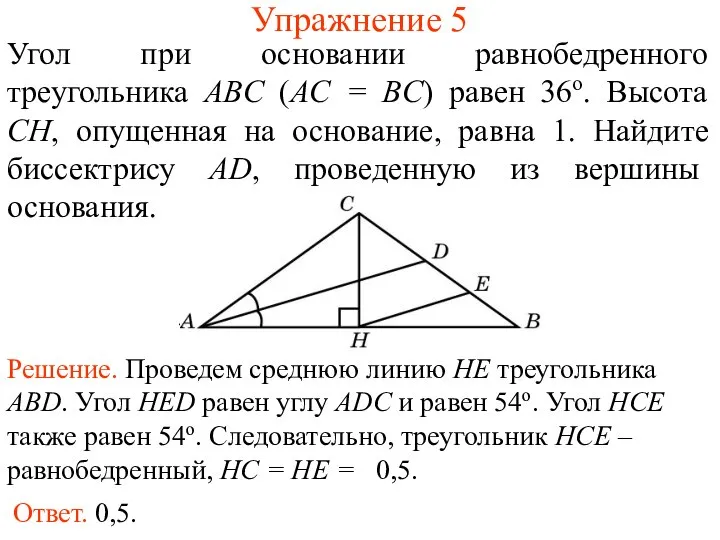
- 19. Упражнение 5 Угол при основании равнобедренного треугольника ABC (AC = BC) равен 36о. Высота CH, опущенная
- 20. Упражнение 6 Найдите радиус окружности, описанной около правильного десятиугольника со стороной 1.
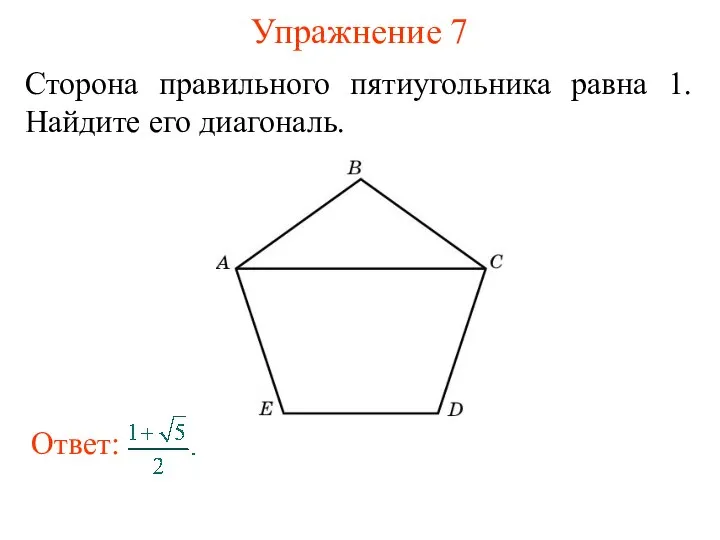
- 21. Упражнение 7 Сторона правильного пятиугольника равна 1. Найдите его диагональ.
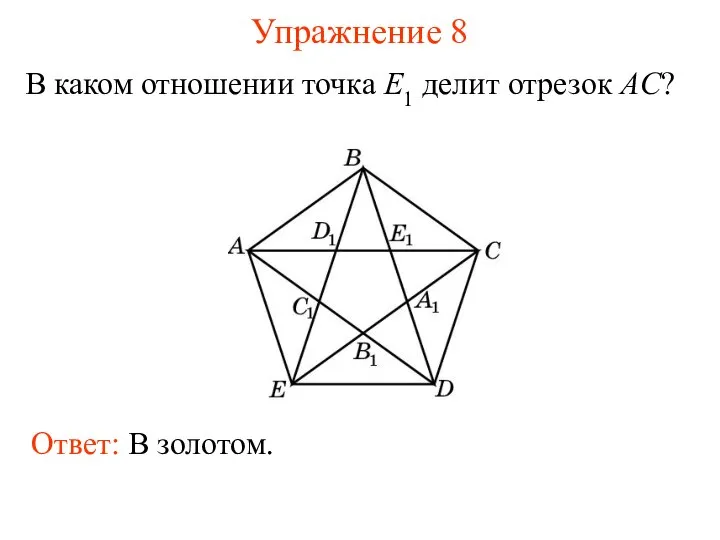
- 22. Упражнение 8 В каком отношении точка E1 делит отрезок AC? Ответ: В золотом.
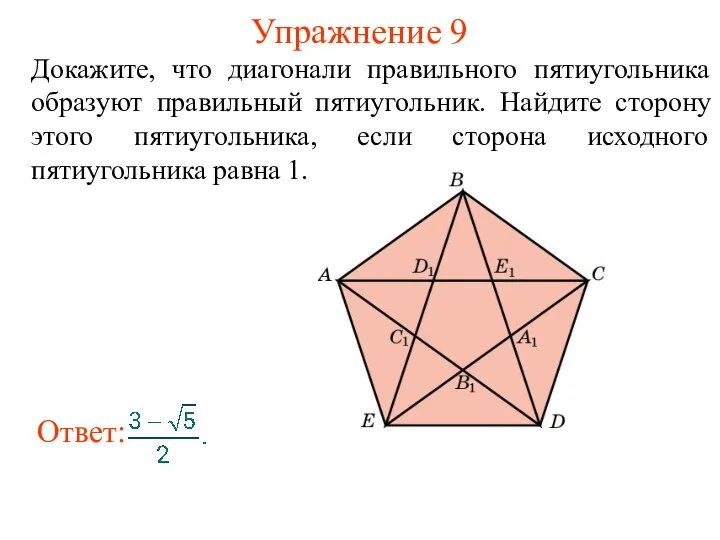
- 23. Упражнение 9 Докажите, что диагонали правильного пятиугольника образуют правильный пятиугольник. Найдите сторону этого пятиугольника, если сторона
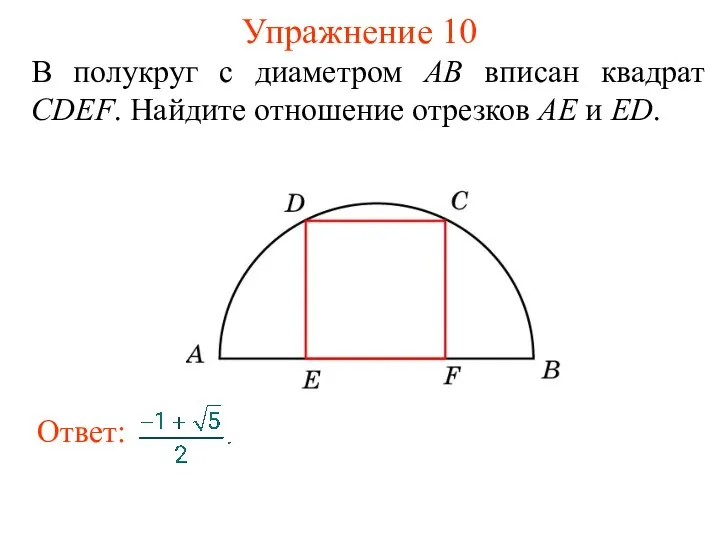
- 24. Упражнение 10 В полукруг с диаметром АВ вписан квадрат CDEF. Найдите отношение отрезков АЕ и ED.
- 25. Упражнение 11 Катет прямоугольного треугольника равен 1. Найдите его гипотенузу, если угол, противолежащий данному катету, равен:
- 26. Упражнение 12 Докажите, что каждый следующий виток золотой спирали подобен предыдущему. Найдите коэффициент подобия.
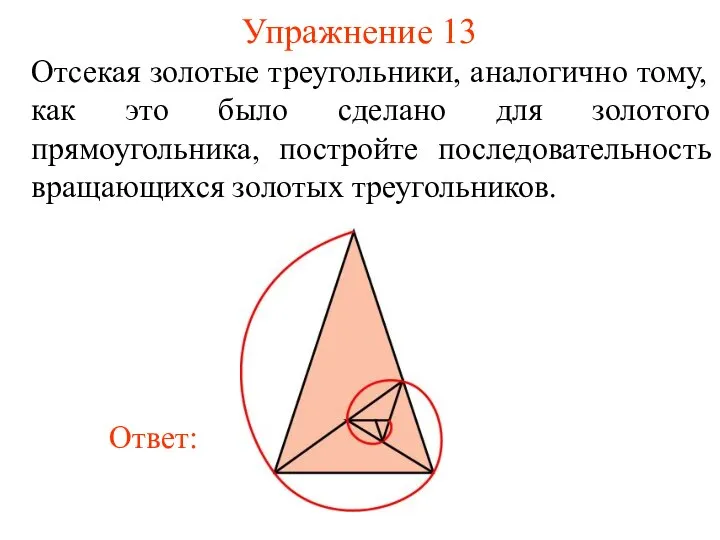
- 27. Упражнение 13 Отсекая золотые треугольники, аналогично тому, как это было сделано для золотого прямоугольника, постройте последовательность
- 29. Скачать презентацию














 Единицы времени. Час. минута
Единицы времени. Час. минута Презентация на тему Тренажер - Табличное умножение и деление
Презентация на тему Тренажер - Табличное умножение и деление  Представьте данные смешанные числа в виде неправильных дробей
Представьте данные смешанные числа в виде неправильных дробей Симметрия. Виды симметрии
Симметрия. Виды симметрии Деление чисел
Деление чисел Презентация на тему Решение простейших тригонометрических уравнений
Презентация на тему Решение простейших тригонометрических уравнений  Уравнение прямой
Уравнение прямой Основы оптимального проектирования
Основы оптимального проектирования Теорема Пифагора. Учебник
Теорема Пифагора. Учебник Замена переменных в определенном интеграле. Лекция 4
Замена переменных в определенном интеграле. Лекция 4 Деление дробных чисел
Деление дробных чисел Уравнение окружности
Уравнение окружности Признаки равенства треугольников
Признаки равенства треугольников Дидактическое сопровождение Развивающаяматематика для 4 класса
Дидактическое сопровождение Развивающаяматематика для 4 класса Вычитание. 5 класс
Вычитание. 5 класс Нелинейная парная регрессия
Нелинейная парная регрессия Презентация на тему Вертикальные и смежные углы
Презентация на тему Вертикальные и смежные углы  Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Формула Бернулли
Формула Бернулли Теорема Пифагора. Задачи на чертежах
Теорема Пифагора. Задачи на чертежах Решение квадратных уравнений
Решение квадратных уравнений Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15 Теорема Пифагора
Теорема Пифагора Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств Формирование элементарных математических представлений
Формирование элементарных математических представлений Геометрия до Евклида
Геометрия до Евклида Взаимно-обратные задачи. 2 класс
Взаимно-обратные задачи. 2 класс