Содержание
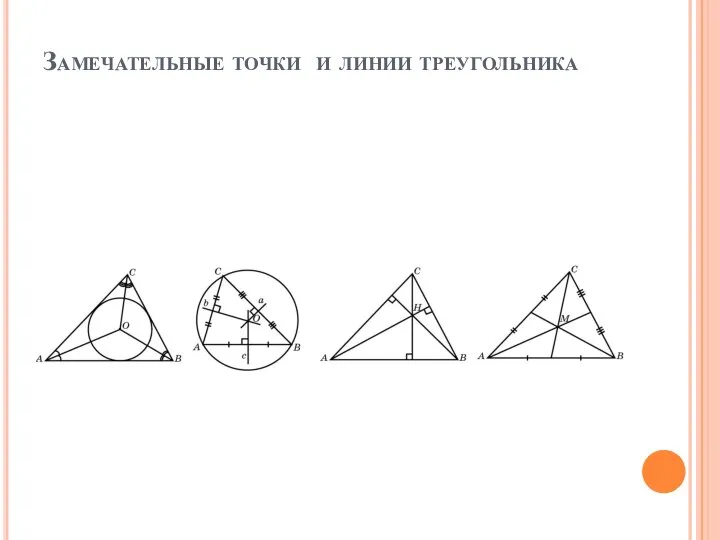
- 2. Замечательные точки и линии треугольника
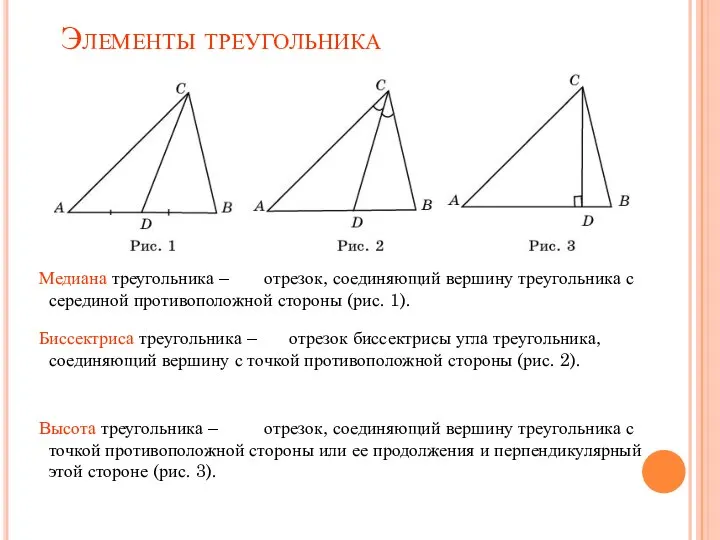
- 3. Элементы треугольника Медиана треугольника – Биссектриса треугольника – Высота треугольника – отрезок, соединяющий вершину треугольника с
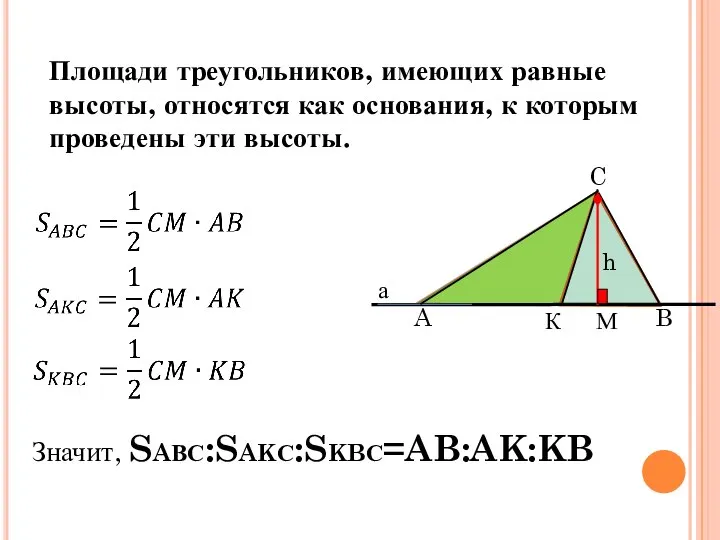
- 4. Значит, SAВС:SAKС:SKBС=AB:AK:KB Пропорциональность площадей Площади треугольников, имеющих равные высоты, относятся как основания, к которым проведены эти
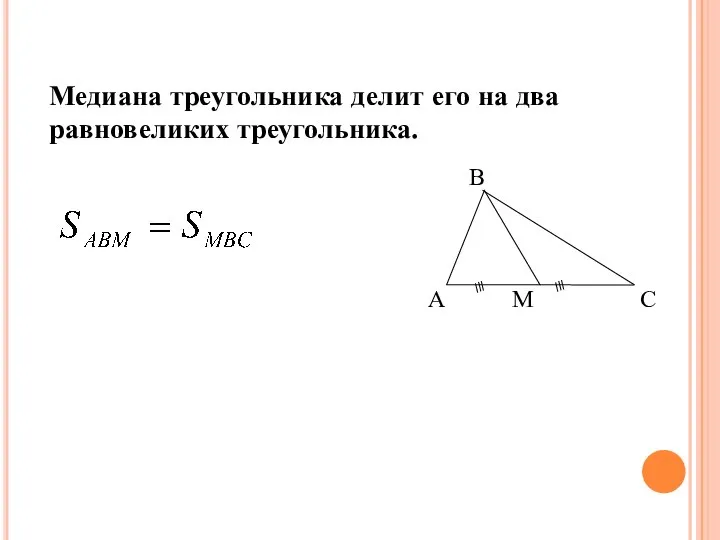
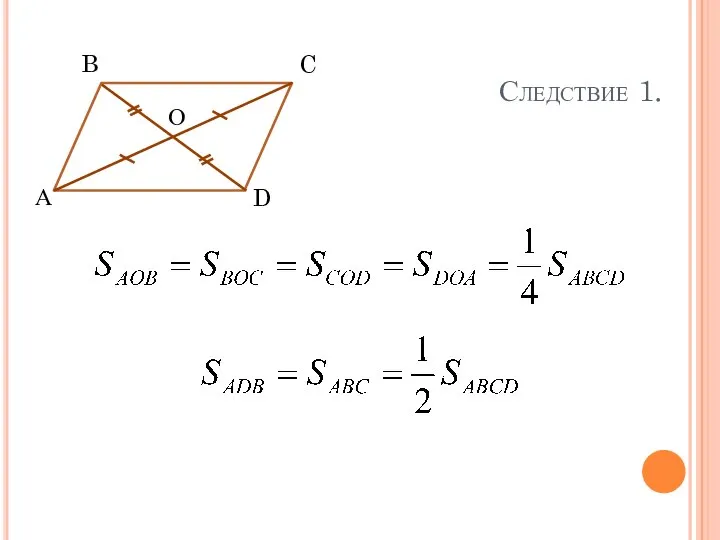
- 5. Медиана треугольника делит его на два равновеликих треугольника. Следствие 1
- 6. А B C D О Рассмотреть на уроке Следствие 1.
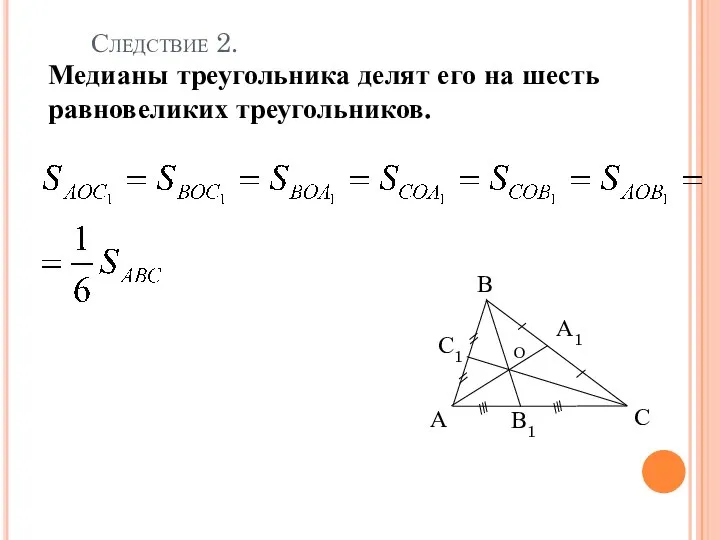
- 7. В Следствие 2 Медианы треугольника делят его на шесть равновеликих треугольников. Следствие 2.
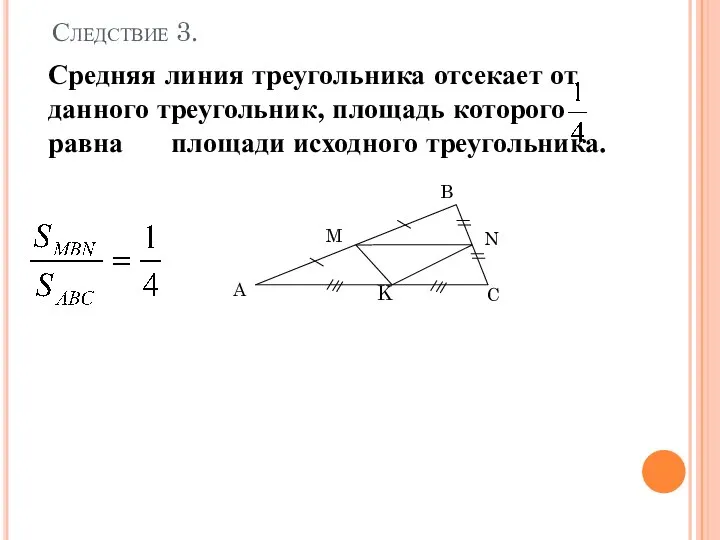
- 8. Доказать на уроке Средняя линия треугольника отсекает от данного треугольник, площадь которого равна площади исходного треугольника.
- 9. Площадь треугольника a b α
- 10. Если угол одного треугольника равен углу другого треугольника, то площади данных треугольников относятся как произведения сторон,
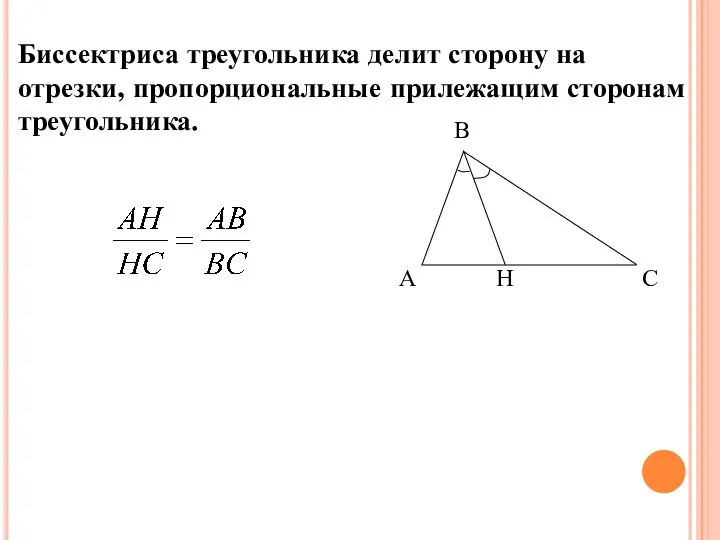
- 11. Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Следствие
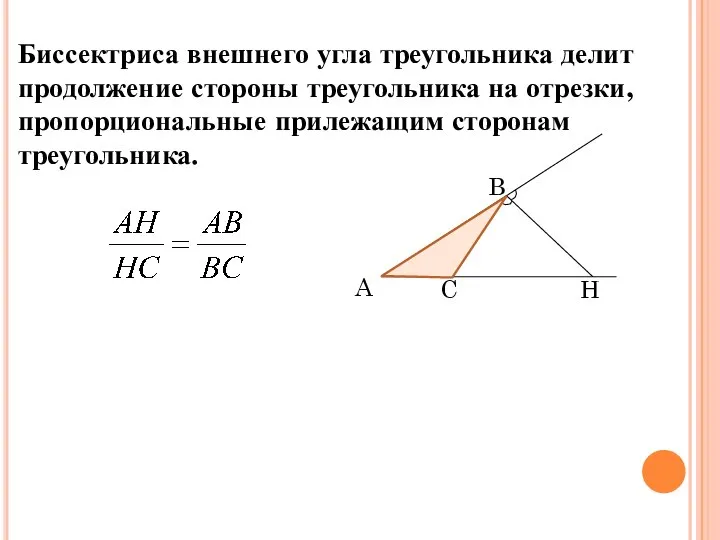
- 12. Биссектриса внешнего угла треугольника делит продолжение стороны треугольника на отрезки, пропорциональные прилежащим сторонам треугольника. Следствие
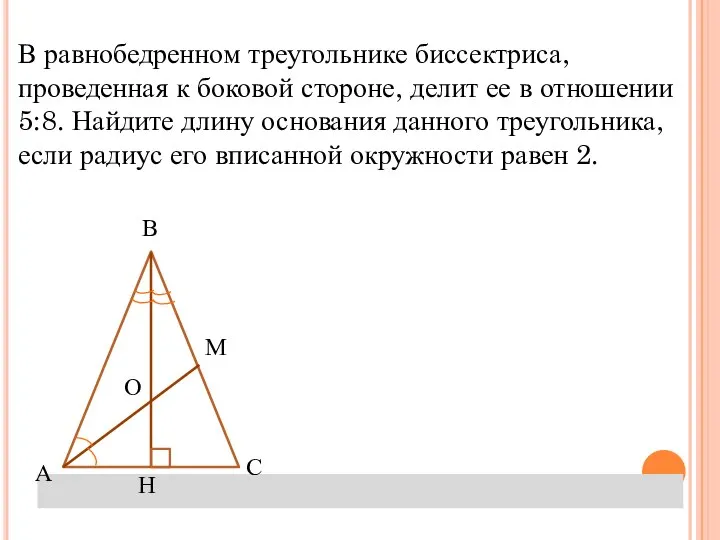
- 13. Задача №4 В равнобедренном треугольнике биссектриса, проведенная к боковой стороне, делит ее в отношении 5:8. Найдите
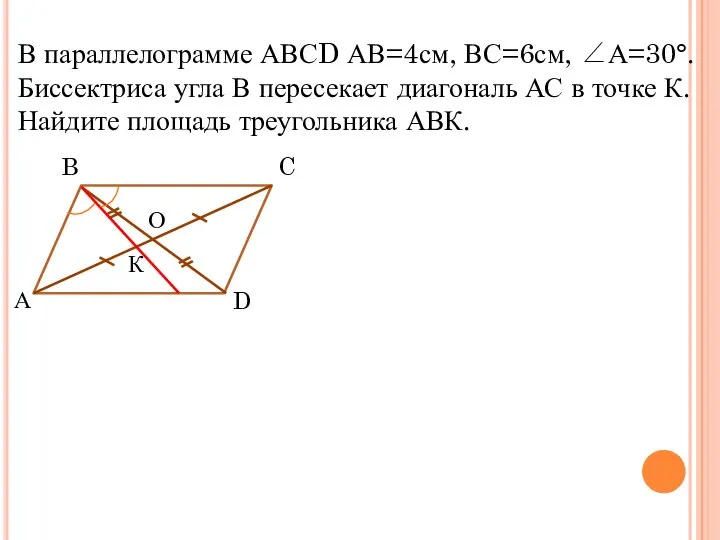
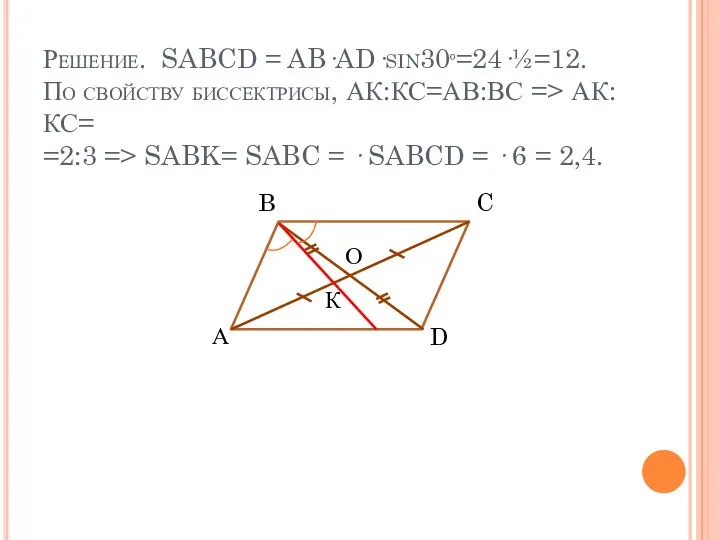
- 14. Задача №5 О В параллелограмме АВСD АВ=4см, ВС=6см, ∠А=30°. Биссектриса угла В пересекает диагональ АС в
- 15. Решение. SABCD = AB·AD·sin30º=24·½=12. По свойству биссектрисы, АК:КС=АВ:ВС => АК:КС= =2:3 => SABK= SABC = ·
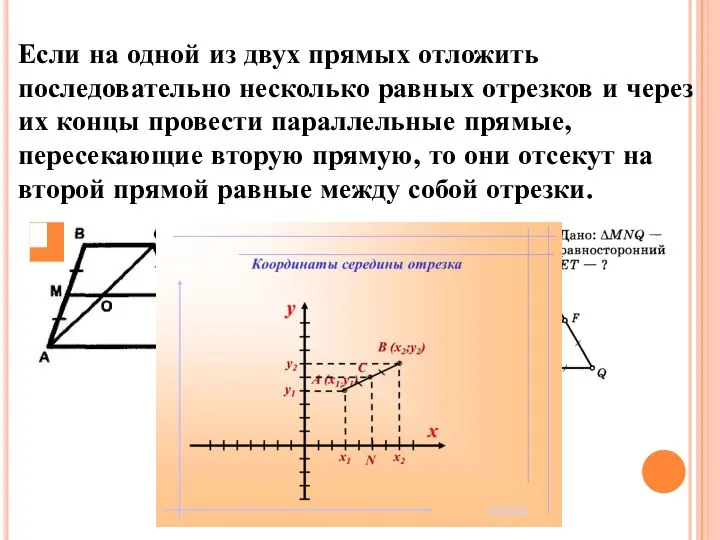
- 16. Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их
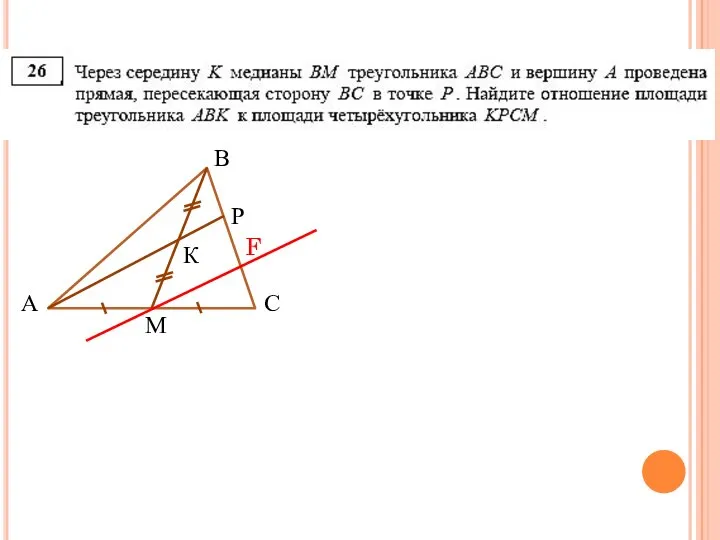
- 17. ГИА 2013 А В С К М Р F
- 19. Скачать презентацию
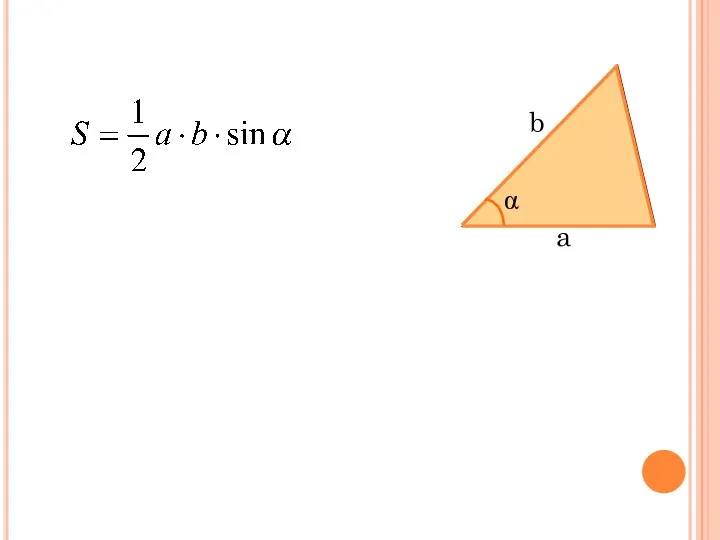

 Прогрессия
Прогрессия Дифференциальные уравнения. Лекция 3
Дифференциальные уравнения. Лекция 3 Метр. (2класс)
Метр. (2класс) Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Число и цифра 5. Дидактическое пособие для детей 4-5 лет
Число и цифра 5. Дидактическое пособие для детей 4-5 лет Симметрия и асимметрия
Симметрия и асимметрия Решение неопределенных интегралов
Решение неопределенных интегралов Занятие 01.10+Задания для п.р
Занятие 01.10+Задания для п.р Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим
Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим Одночлен и его стандартный вид
Одночлен и его стандартный вид Числовая окружность. Занятие 1-2
Числовая окружность. Занятие 1-2 Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Тригонометрия. Учебно-игровое пособие
Тригонометрия. Учебно-игровое пособие Предел функции
Предел функции Скалярное произведение векторов. Решение задач
Скалярное произведение векторов. Решение задач Анализ данных. Описательные статистики
Анализ данных. Описательные статистики Понятие корня
Понятие корня Международный день головоломки
Международный день головоломки Собери съедобные грибы в корзинку
Собери съедобные грибы в корзинку Презентация на тему Упрощение выражений (5 класс)
Презентация на тему Упрощение выражений (5 класс)  Религия Байеса
Религия Байеса Пересечение поверхностей
Пересечение поверхностей Теория вероятностей
Теория вероятностей Учимся писать цифры
Учимся писать цифры Методика прикладных вычислений в конечных полях
Методика прикладных вычислений в конечных полях Свойства тригонометрических функций и их графики
Свойства тригонометрических функций и их графики Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА
Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА