Двугранный угол. Перпендикулярность плоскостей

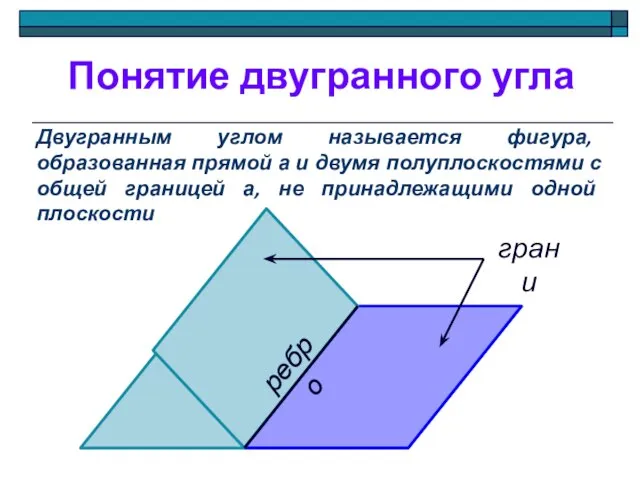
Понятие двугранного угла
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости
ребро
грани

Применение двугранных углов

Применение двугранных углов

Применение двугранных углов

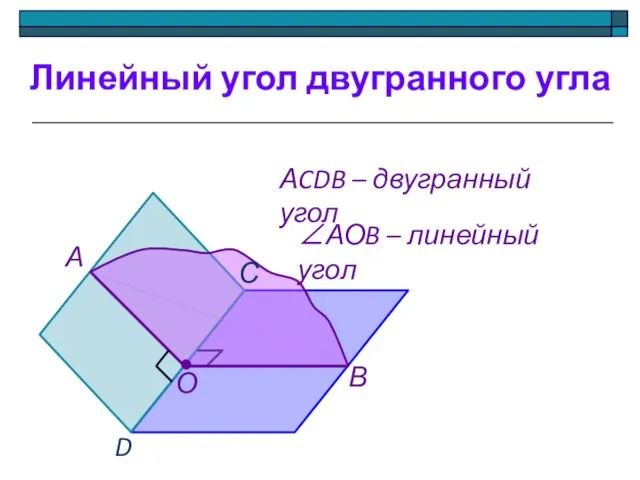
Линейный угол двугранного угла
А
В
О
D
С
АCDB – двугранный угол
∠АОB – линейный угол

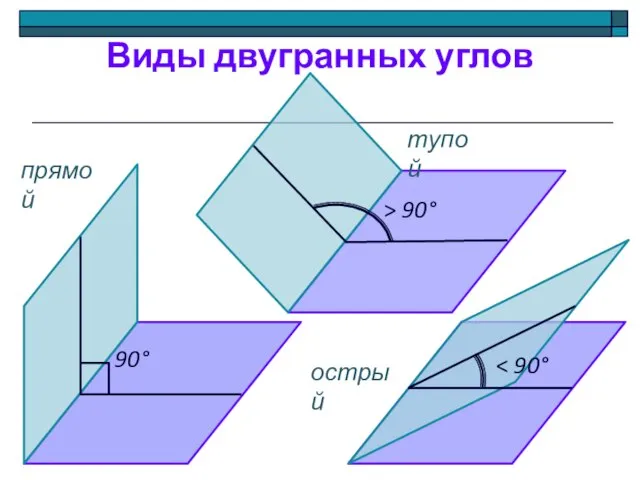
Виды двугранных углов
90°
> 90°
< 90°
острый
тупой
прямой

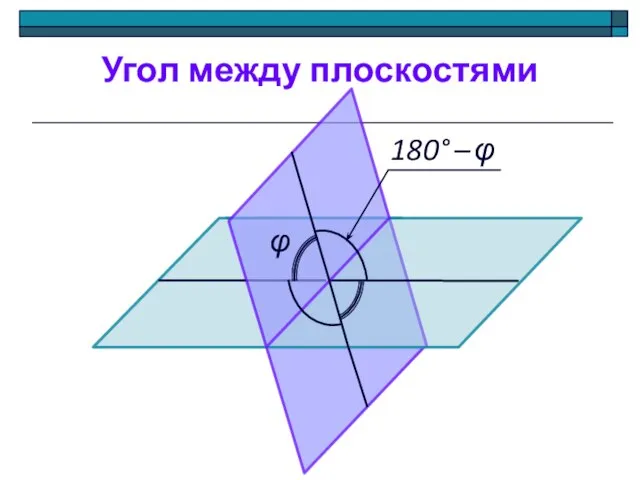
Угол между плоскостями
φ
180° – φ

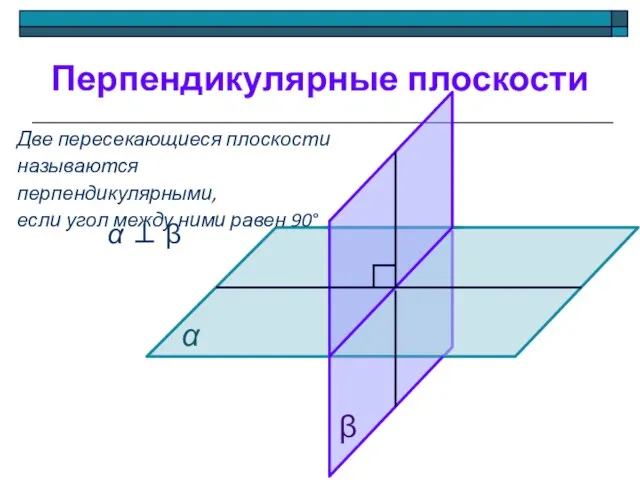
Перпендикулярные плоскости
Две пересекающиеся плоскости
называются перпендикулярными,
если угол между ними равен 90°
α
α ⊥ β
β

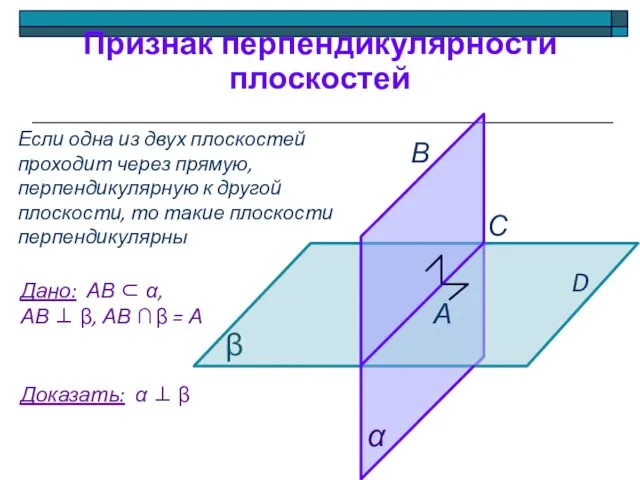
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны
β
А
В
D
С
α
Дано: АВ ⊂ α,
АВ ⊥ β, АВ ∩ β = А
Доказать: α ⊥ β

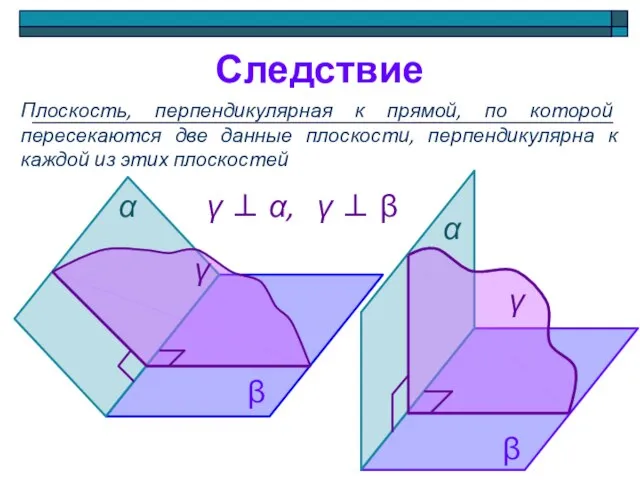
Следствие
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей
α
γ
β
β
α
γ
γ ⊥ α, γ ⊥ β

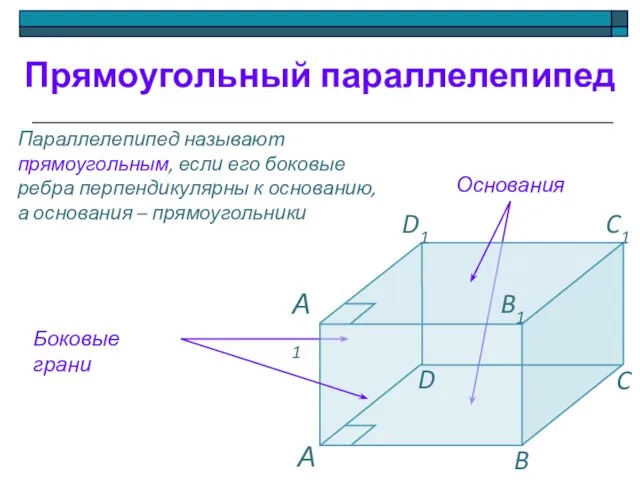
Прямоугольный параллелепипед
Параллелепипед называют прямоугольным, если его боковые ребра перпендикулярны к основанию,
а основания – прямоугольники
Основания
Боковые грани

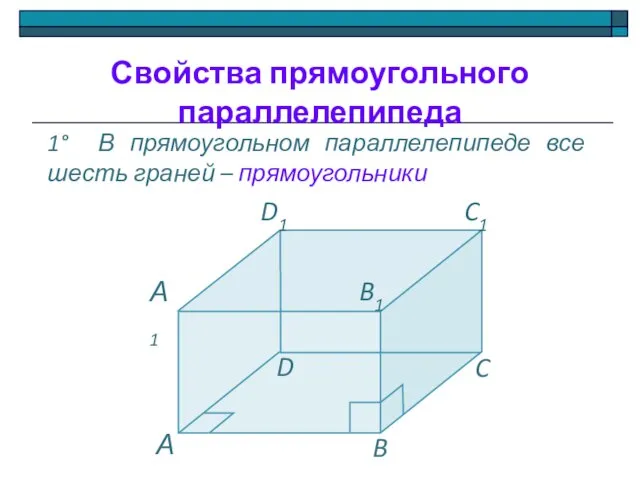
Свойства прямоугольного параллелепипеда
1° В прямоугольном параллелепипеде все шесть граней – прямоугольники

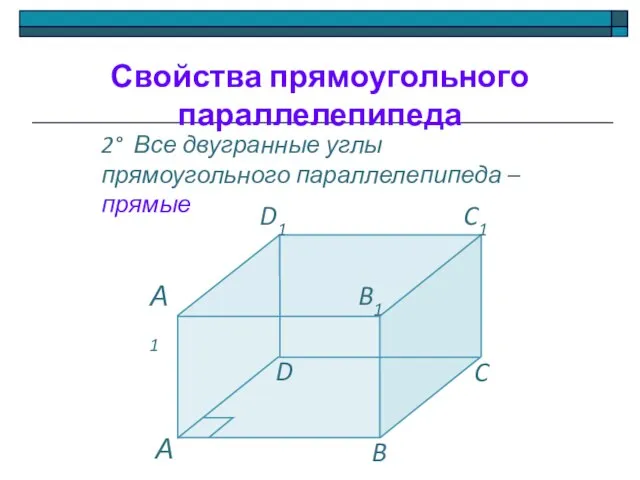
2° Все двугранные углы прямоугольного параллелепипеда – прямые
Свойства прямоугольного параллелепипеда

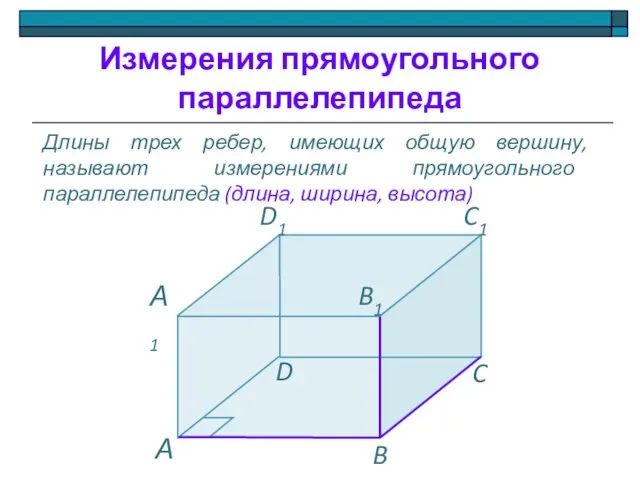
Длины трех ребер, имеющих общую вершину, называют измерениями прямоугольного параллелепипеда (длина, ширина, высота)
Измерения прямоугольного параллелепипеда

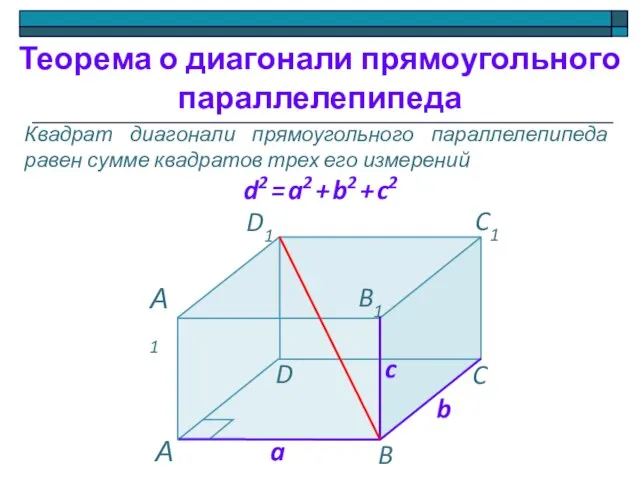
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений
d2 = a2 + b2 + c2
Теорема о диагонали прямоугольного параллелепипеда
a
b
c

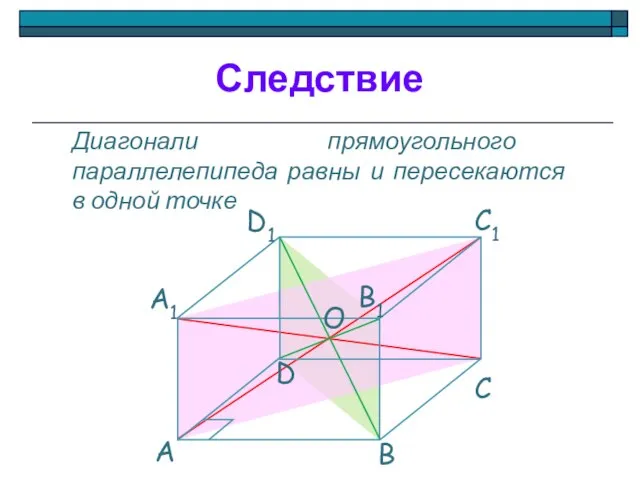
Диагонали прямоугольного параллелепипеда равны и пересекаются в одной точке
Следствие
О