Содержание
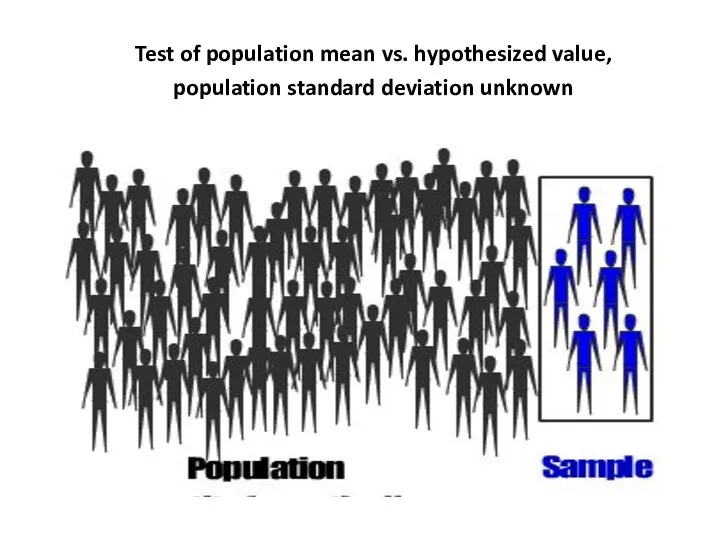
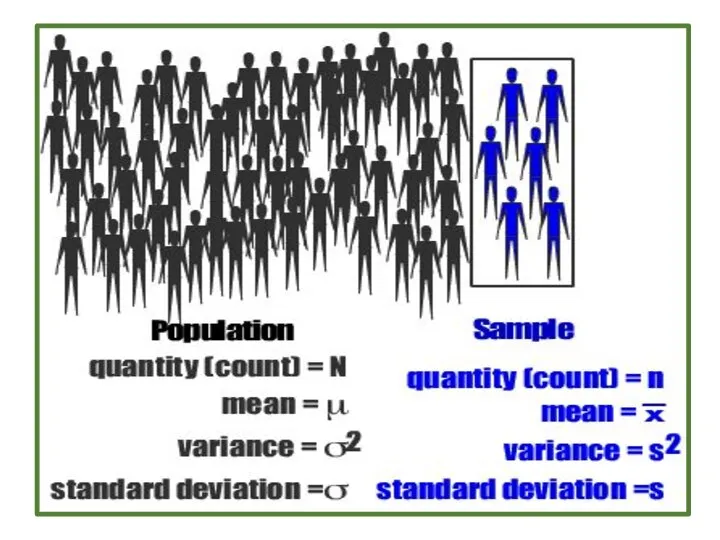
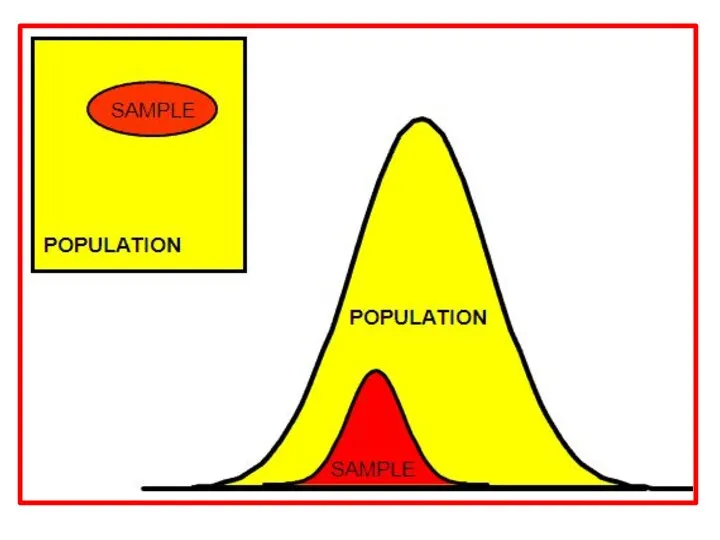
- 2. Test of population mean vs. hypothesized value, population standard deviation unknown
- 5. Exercise (13)
- 6. Exercise (13): It is known that the mean Haemoglobin percent (Hb%) of adult females in a
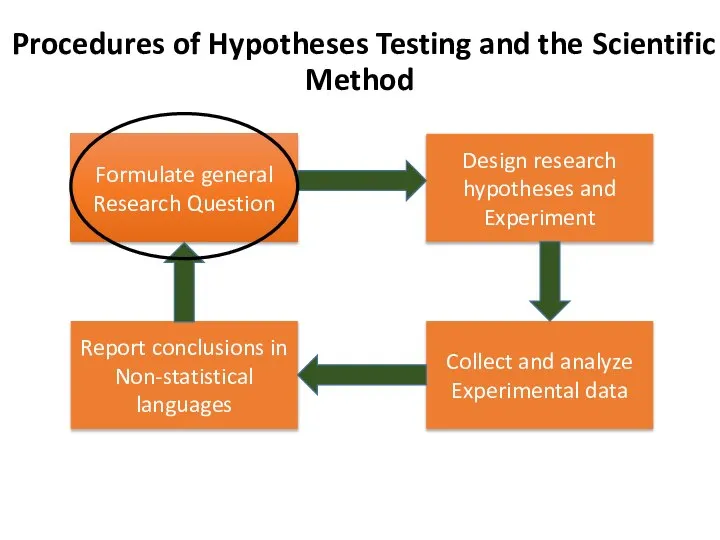
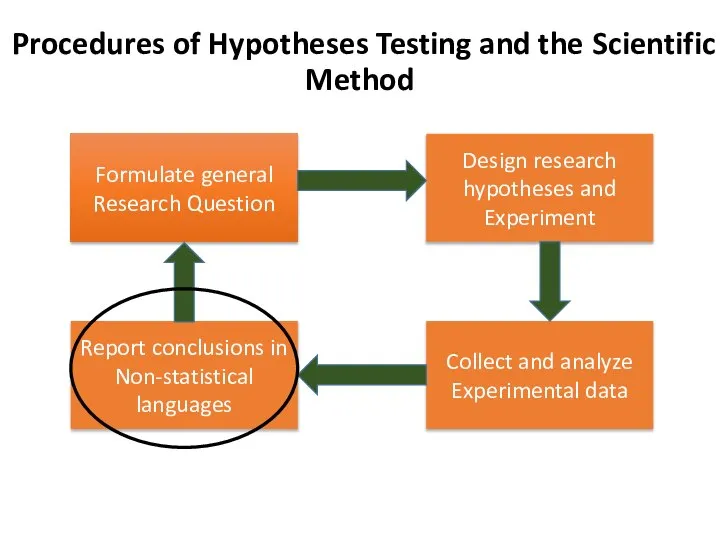
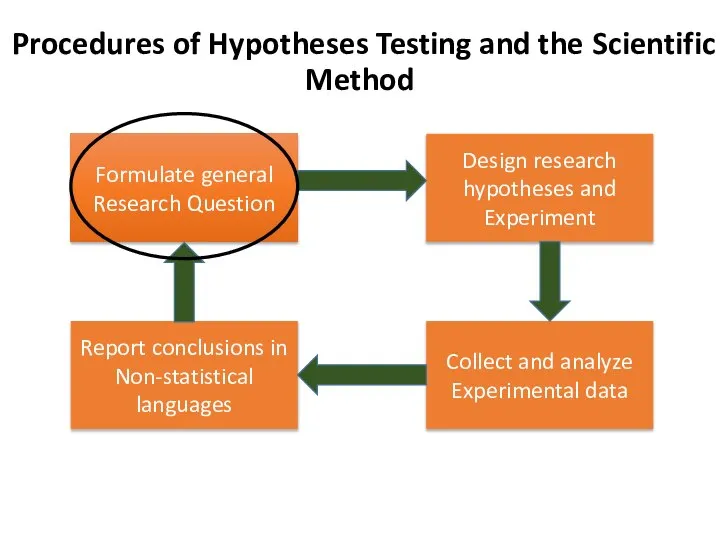
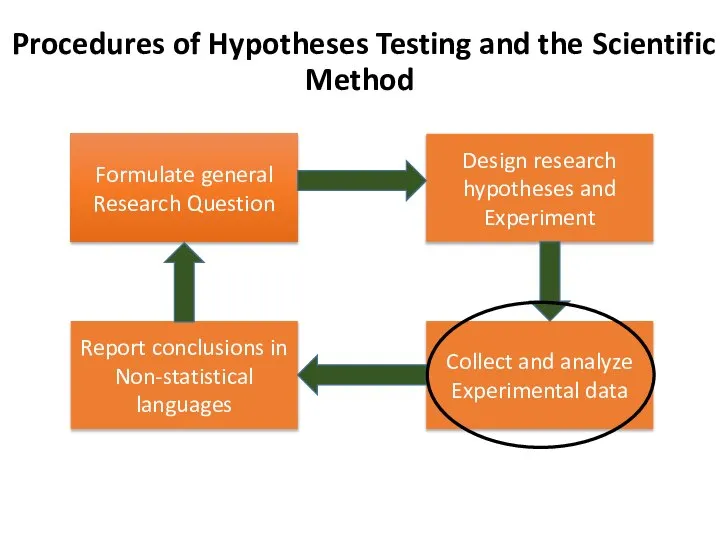
- 7. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 8. I. Formulate general Research Question Does pregnancy have significant effect on mean Hb%?
- 9. I. Formulate general Research Question Does pregnancy have significant effect on mean Hb%?
- 10. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 11. II. State Research Hypotheses Ho: µ = X (pregnancy has no significant effect on mean Hb%)
- 12. II. State Research Hypotheses Ho: µ = X (pregnancy has no significant effect on mean Hb%)
- 13. II. State Research Hypotheses Ho: µ = X (pregnancy has no significant effect on mean Hb%)
- 14. II. State Research Hypotheses Ho: µ = X (pregnancy has no significant effect on mean Hb%)
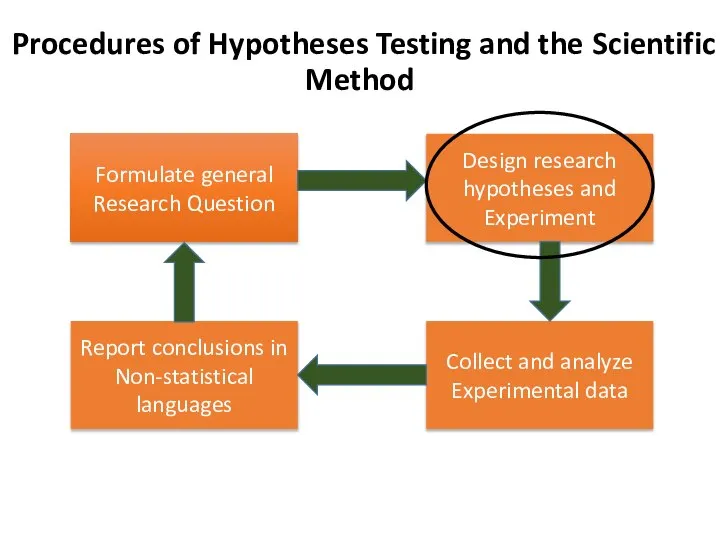
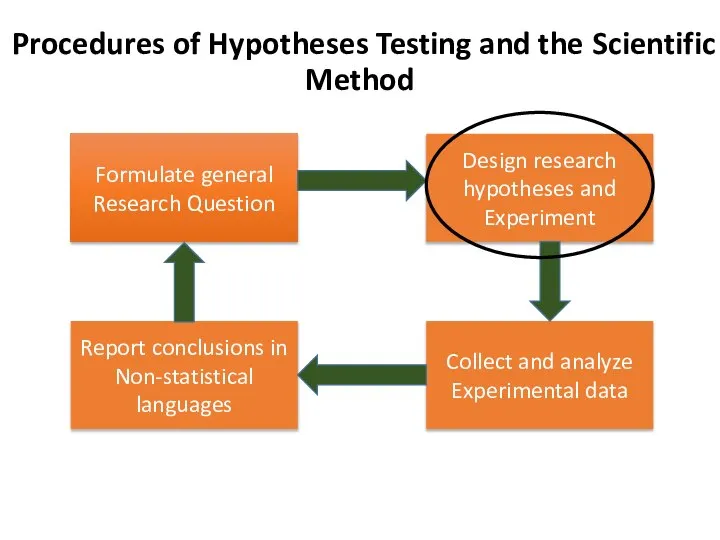
- 15. Design Research Hypotheses and Experiment
- 16. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 17. V. Calculate test statistic VI. Make a Decision regarding Research Hypotheses (Specify the Decision Method) Reject
- 18. V. Calculate test statistic VI. Make a Decision regarding Research Hypotheses (Specify the Decision Method) Reject
- 19. V. Calculate test statistic VI. Make a Decision regarding Research Hypotheses (Specify the Decision Method) Reject
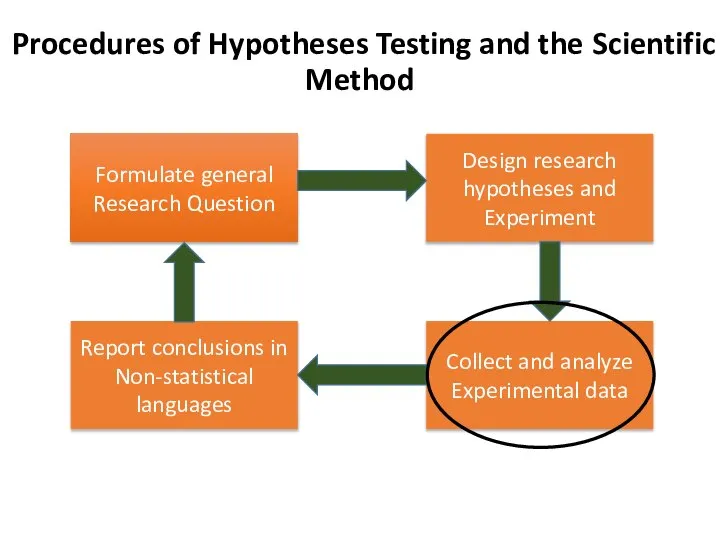
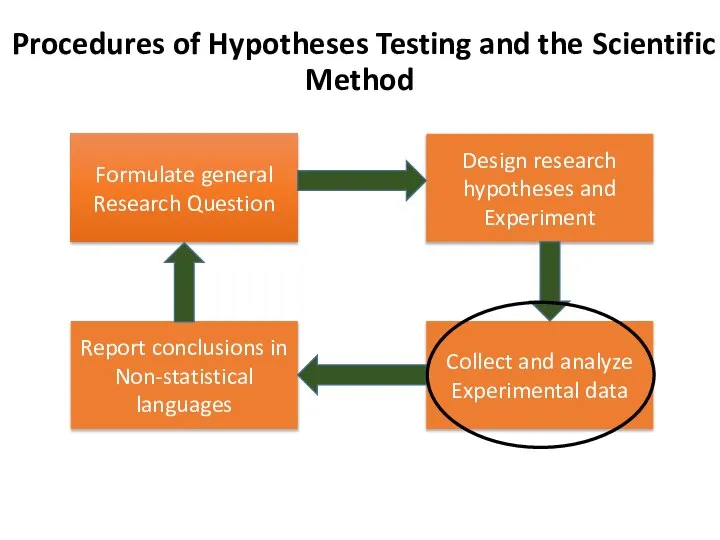
- 20. Collect and Analyze Experimental Data
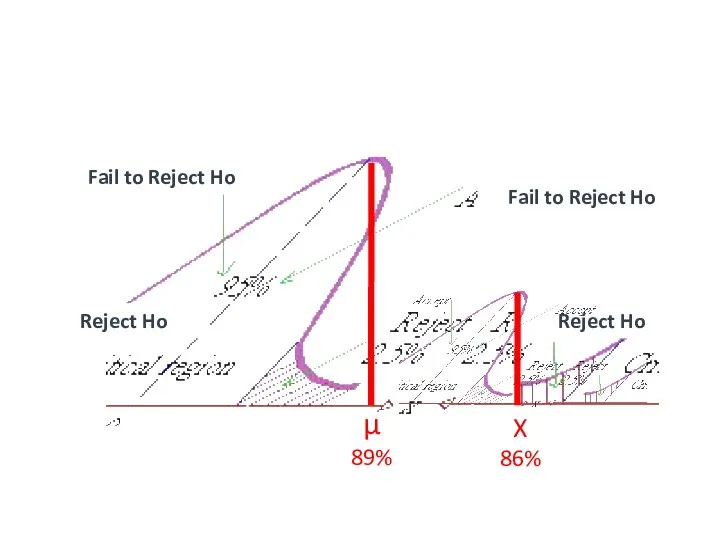
- 22. Reject Ho Fail to Reject Ho Fail to Reject Ho Reject Ho +1.96 -1.96 µ 89%
- 23. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
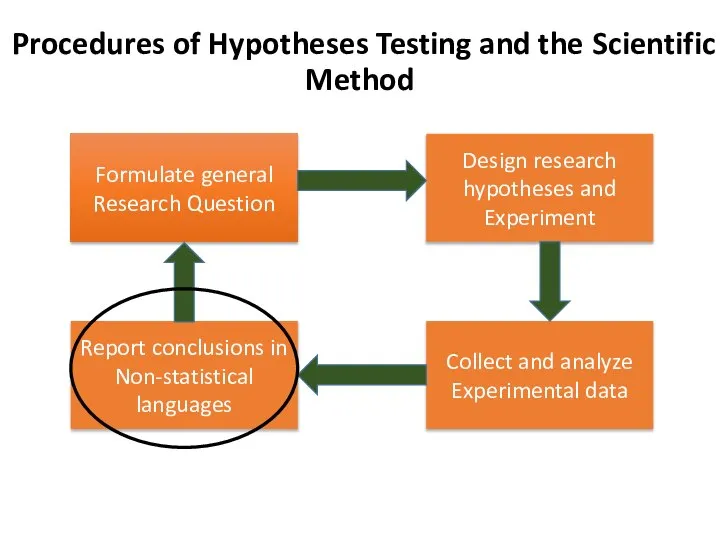
- 24. VII. Report a conclusion Pregnancy has a significant effect on mean Hb%. The mean Hb% of
- 25. VII. Report a conclusion Pregnancy has a significant effect on mean Hb%. The mean Hb% of
- 26. Comparing Means (Parametric tests) One Population Inference Two Population Inference Independent Sampling Model Dependent Sampling Model
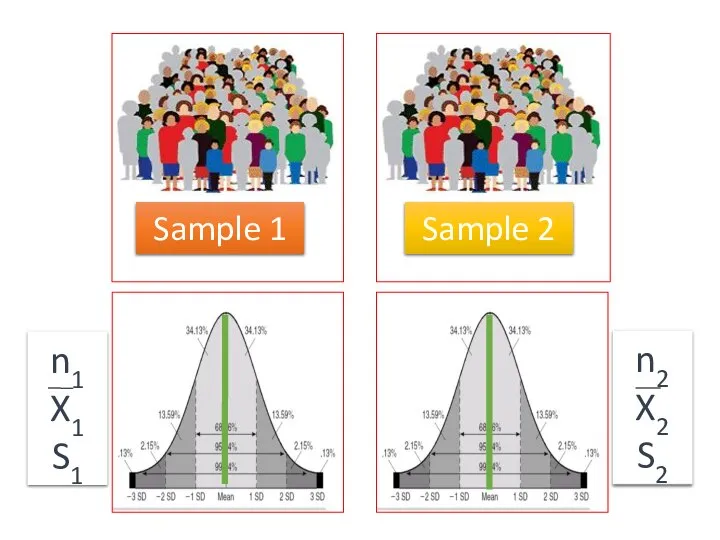
- 27. Sample 1 Sample 2 The data is collected by two simple random samples from separate and
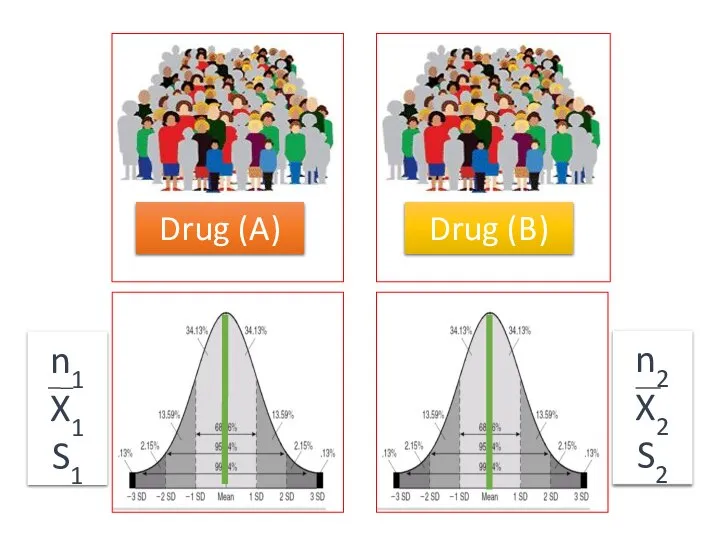
- 28. Sample 1 Sample 2 n1 X1 S1 n2 X2 S2
- 29. Exercise (14)
- 30. Researchers were motivated to test a new antihypertensive drug (A) on a group of patients. They
- 31. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 32. I. Formulate general Research Question Does pregnancy have significant effect on mean Hb%?
- 33. I. Formulate general Research Question Is there any significant difference in the mean reduction of systolic
- 34. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 35. II. State Research Hypotheses Ho: X1 = X2 There is no significant difference in the mean
- 36. II. State Research Hypotheses Ho: X1 = X2 There is no significant difference in the mean
- 37. II. State Research Hypotheses Ho: X1 = X2 There is no significant difference in the mean
- 38. II. State Research Hypotheses Ho: X1 = X2 There is no significant difference in the mean
- 39. Design Research Hypotheses and Experiment
- 40. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 41. V. Make a Decision regarding Research Hypotheses (Specify the Decision Method) Fail to Reject Null Hypothesis
- 42. Collect and Analyze Experimental Data
- 43. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
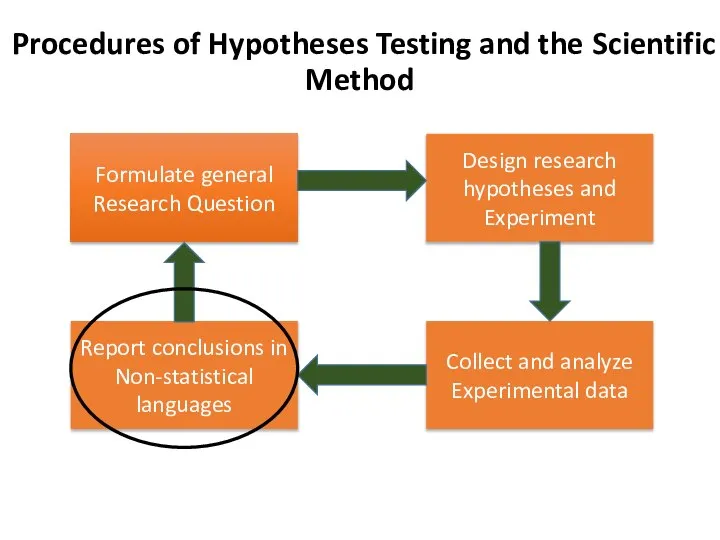
- 44. VI. Report a conclusion Pregnancy has a significant effect on mean Hb%. The mean Hb% of
- 45. VI. Report a conclusion There is insufficient evidence to support the claim that there is a
- 46. Drug (A) Drug (B) n1 X1 S1 n2 X2 S2
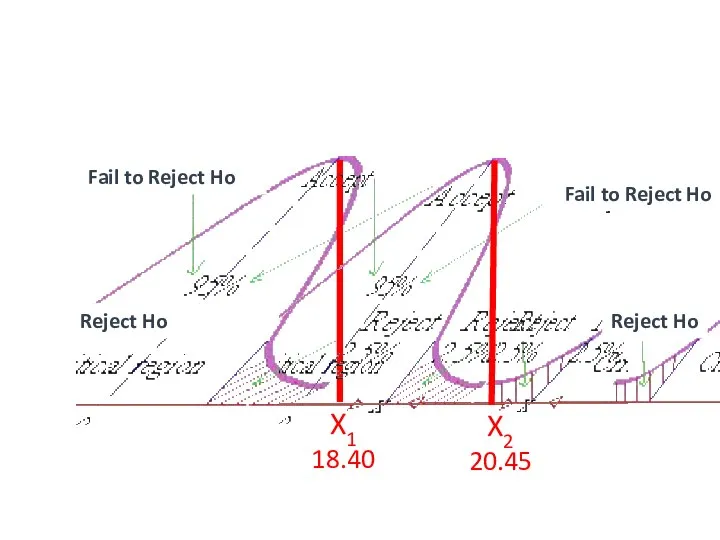
- 47. +1.96 -1.96 X1 9 X2 12 Fail to Reject Ho Reject Ho Reject Ho Fail to
- 48. Comparing Means (Parametric tests) One Population Inference Two Population Inference Independent Sampling Model Dependent Sampling Model
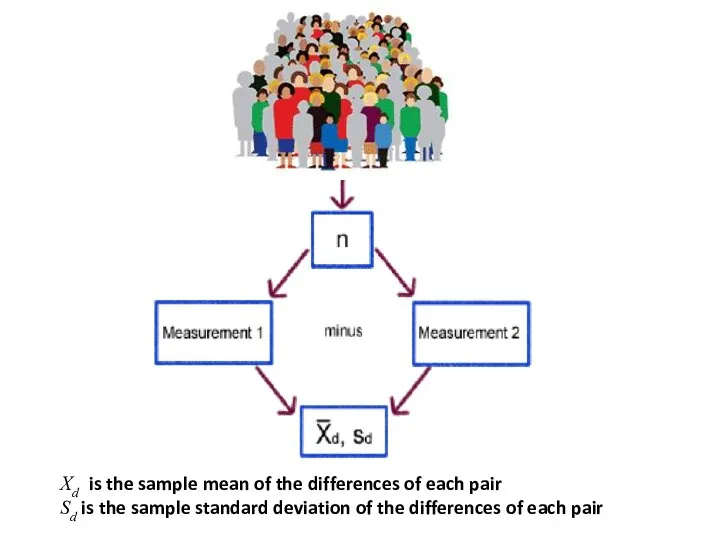
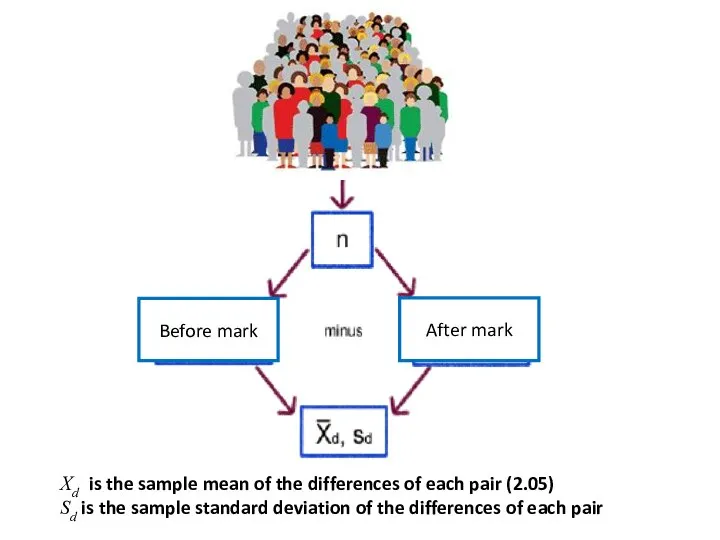
- 49. Sample The data consists of a single population and two measurements. A simple random sample is
- 50. Xd is the sample mean of the differences of each pair Sd is the sample standard
- 51. Matched pairs t-test compares the means for two dependent populations (paired difference t-test) Model Assumptions Variable
- 52. Matched pairs t-test compares the means for two dependent populations (paired difference t-test) Test Statistic Xd
- 53. Exercise (15)
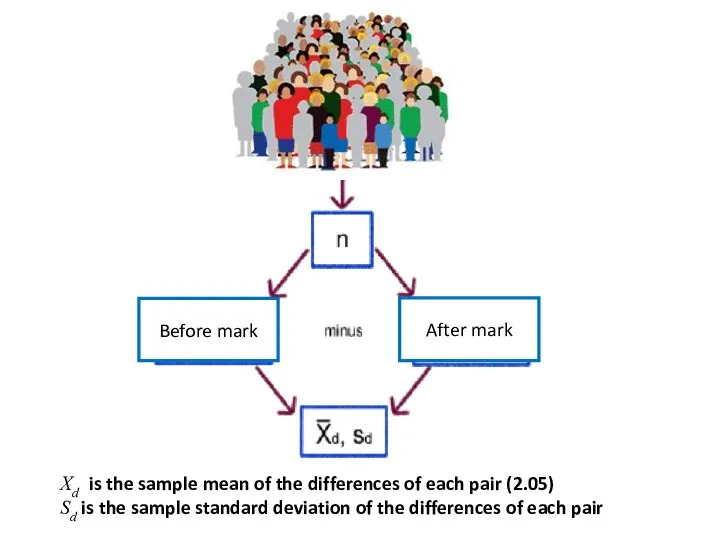
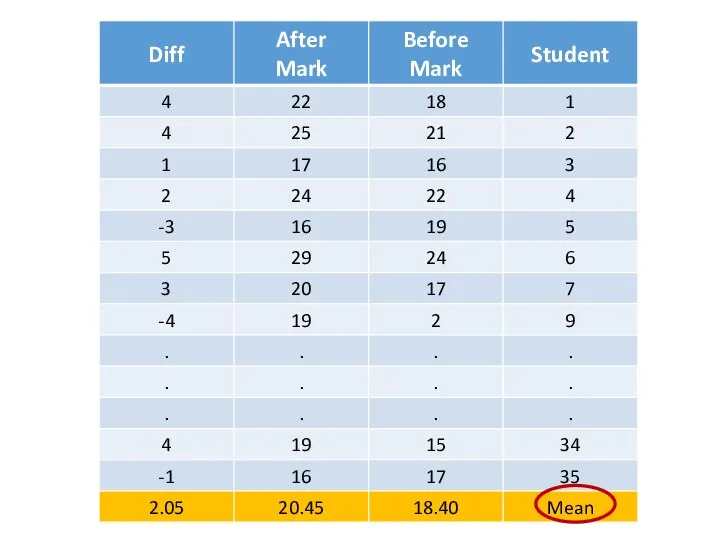
- 54. Exercise (15): An instructor of Anatomy course wants to know if student marks are different on
- 55. Xd is the sample mean of the differences of each pair (2.05) Sd is the sample
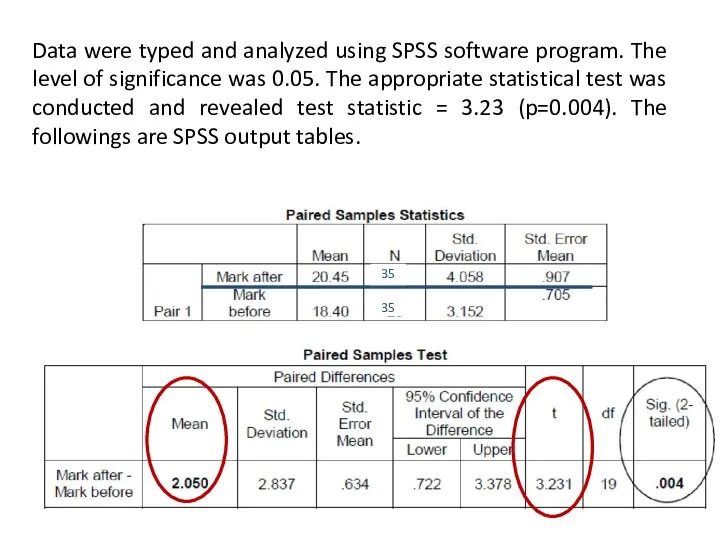
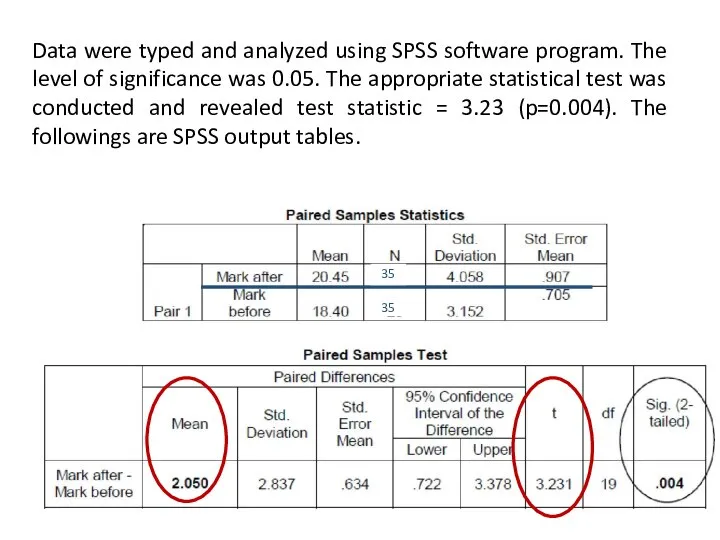
- 57. Data were typed and analyzed using SPSS software program. The level of significance was 0.05. The
- 58. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 59. I. Formulate general Research Question Does pregnancy have significant effect on mean Hb%?
- 60. I. Formulate general Research Question Is there a difference in students’ marks following implementation of TBL
- 61. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 62. II. State Research Hypotheses Ho: There is no difference in mean pre- and post-TBL marks H1:
- 63. II. State Research Hypotheses Ho: There is no difference in mean pre- and post-TBL marks H1:
- 64. II. State Research Hypotheses Ho: There is no difference in mean pre- and post-TBL marks H1:
- 65. II. State Research Hypotheses Ho: There is no difference in mean pre- and post-TBL marks H1:
- 66. Design Research Hypotheses and Experiment
- 67. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 68. Collect and Analyze Experimental Data
- 69. V. Make a Decision regarding Research Hypotheses (Specify the Decision Method) Reject Null Hypothesis Ho P-value
- 70. Data were typed and analyzed using SPSS software program. The level of significance was 0.05. The
- 71. V. Make a Decision regarding Research Hypotheses (Specify the Decision Method) Reject Null Hypothesis Ho P-value
- 72. Formulate general Research Question Procedures of Hypotheses Testing and the Scientific Method Design research hypotheses and
- 73. VI. Report a conclusion Pregnancy has a significant effect on mean Hb%. The mean Hb% of
- 74. VI. Report a conclusion There is a strong evidence (t = 3.23, p = 0.004) that
- 75. Xd is the sample mean of the differences of each pair (2.05) Sd is the sample
- 76. +1.96 -1.96 X1 18.40 X2 20.45 Fail to Reject Ho Reject Ho Reject Ho Fail to
- 77. Comparing Means (Parametric tests) One Population Inference Two Population Inference Independent Sampling Model Dependent Sampling Model
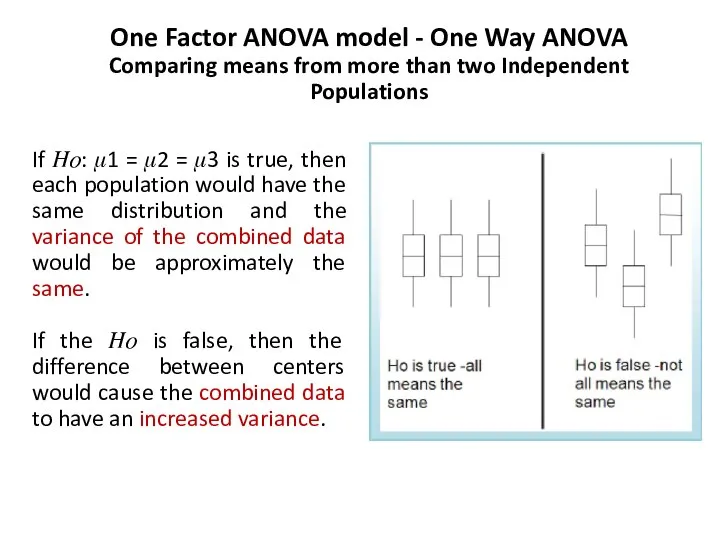
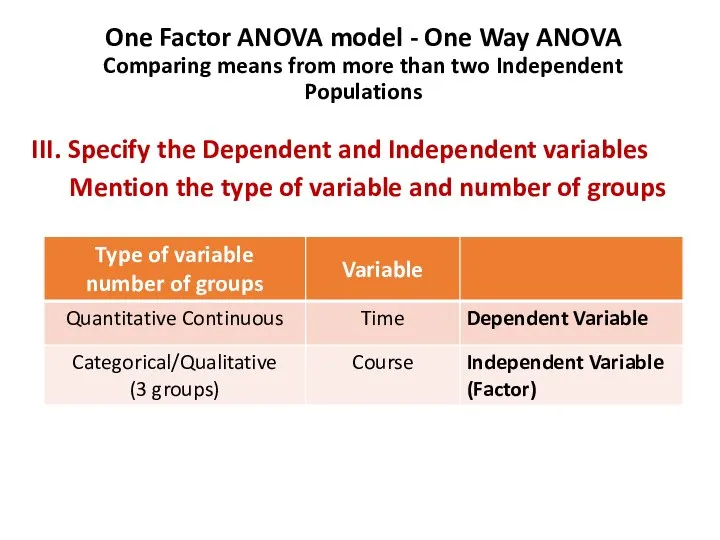
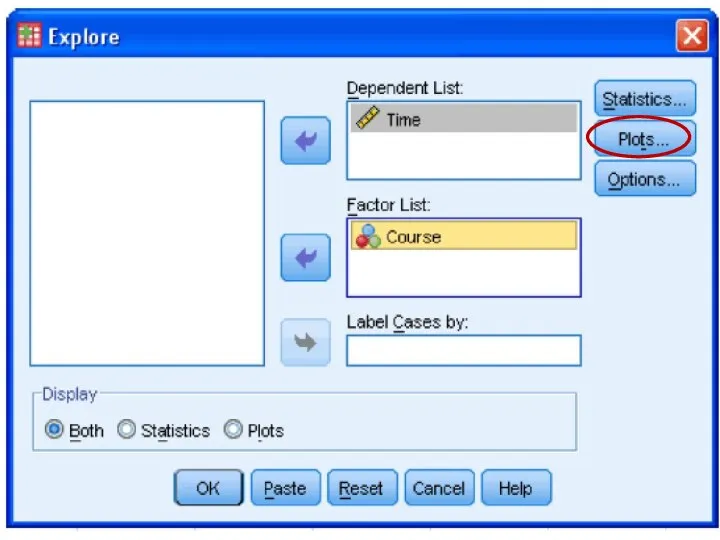
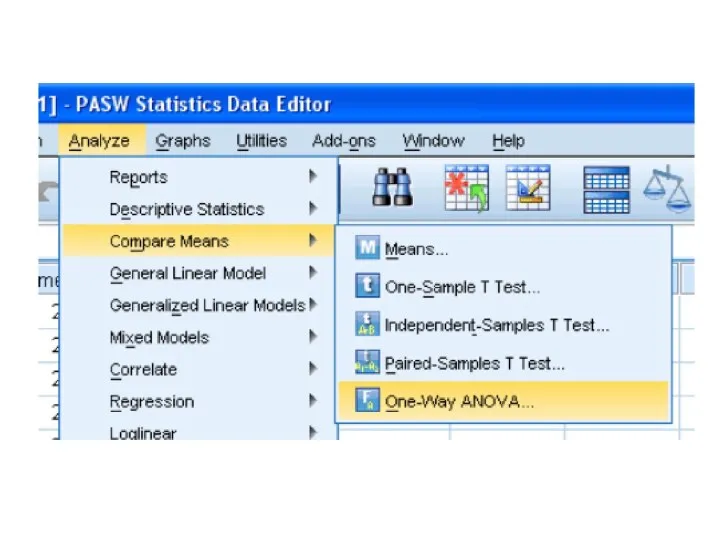
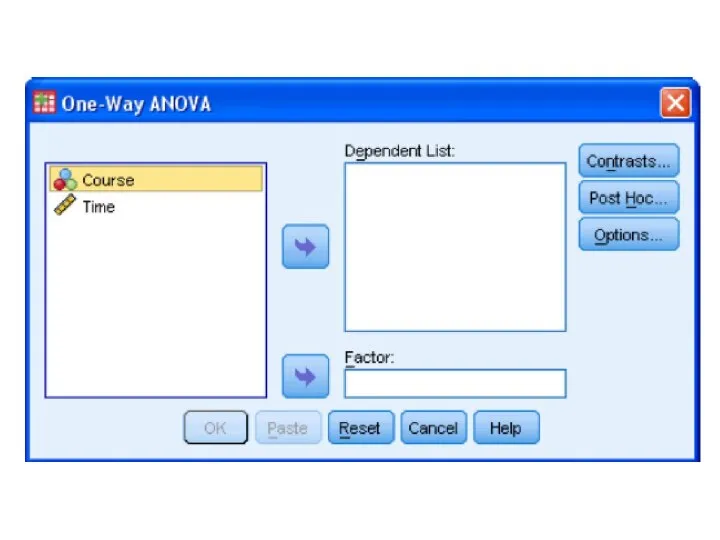
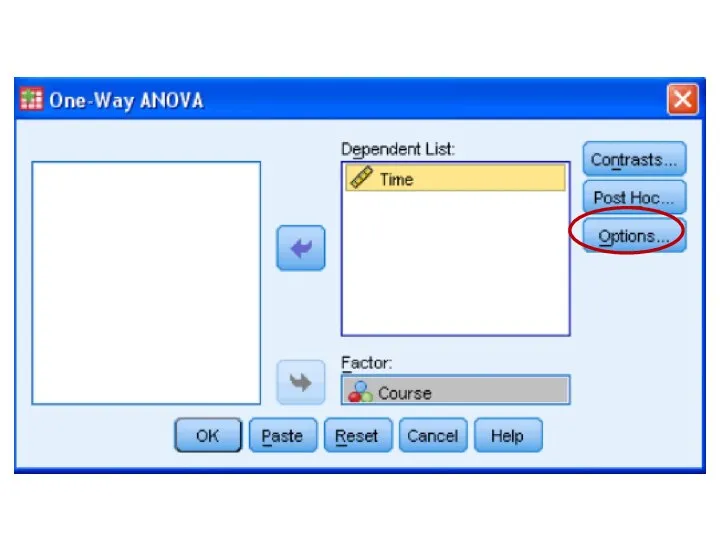
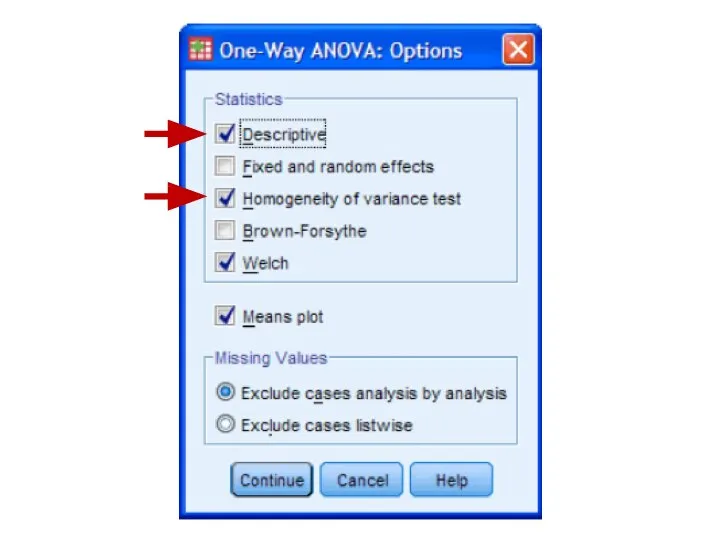
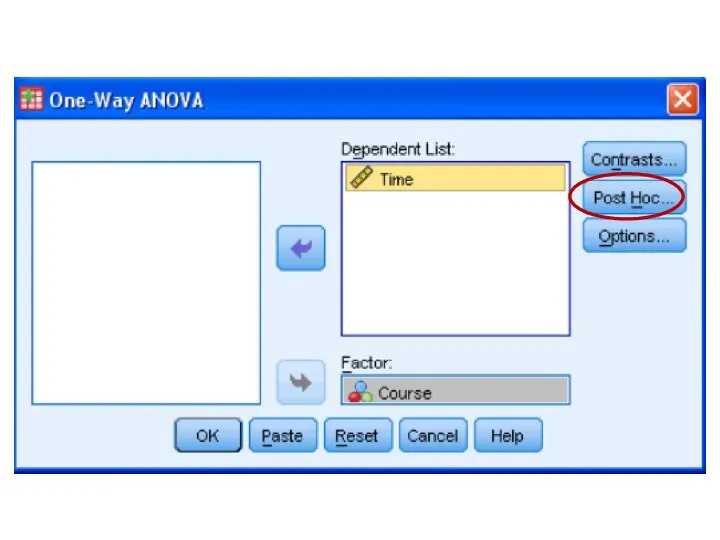
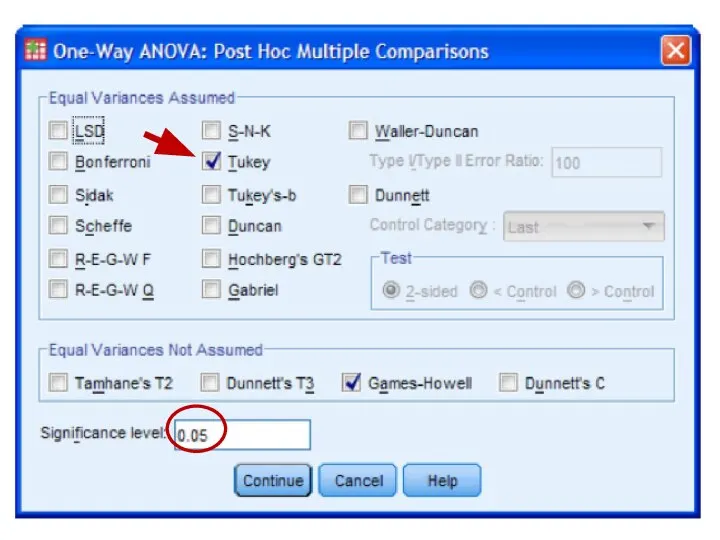
- 78. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 79. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 80. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
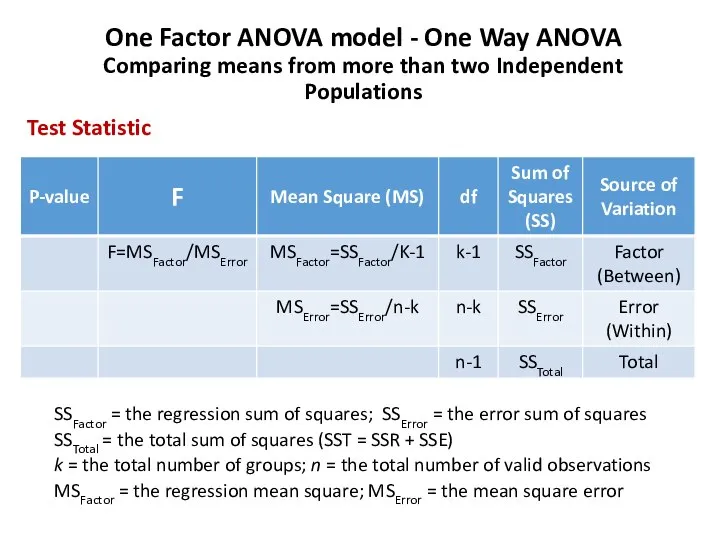
- 81. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 82. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 83. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 84. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 85. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
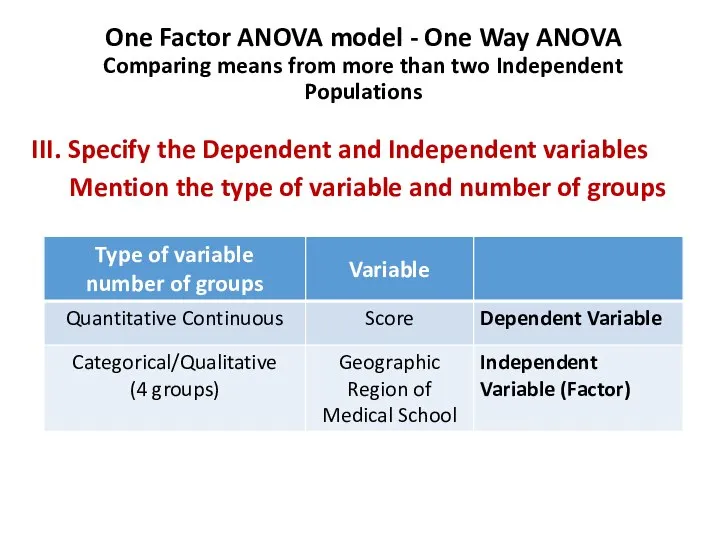
- 86. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 87. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 88. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 89. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 90. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 91. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 92. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
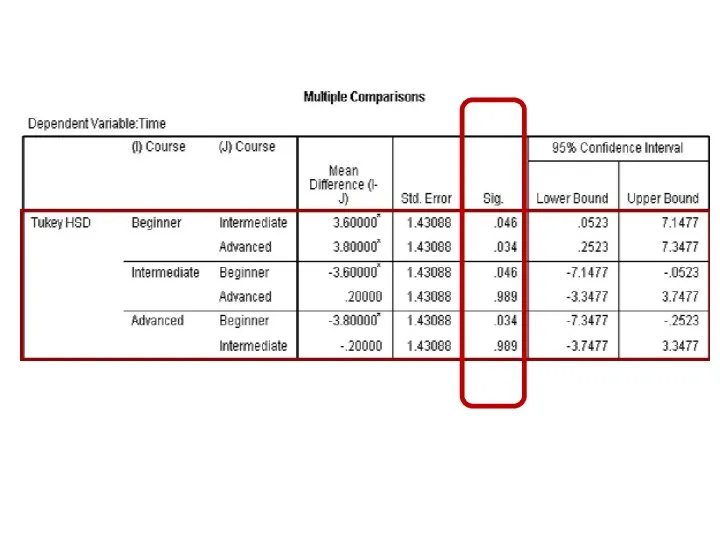
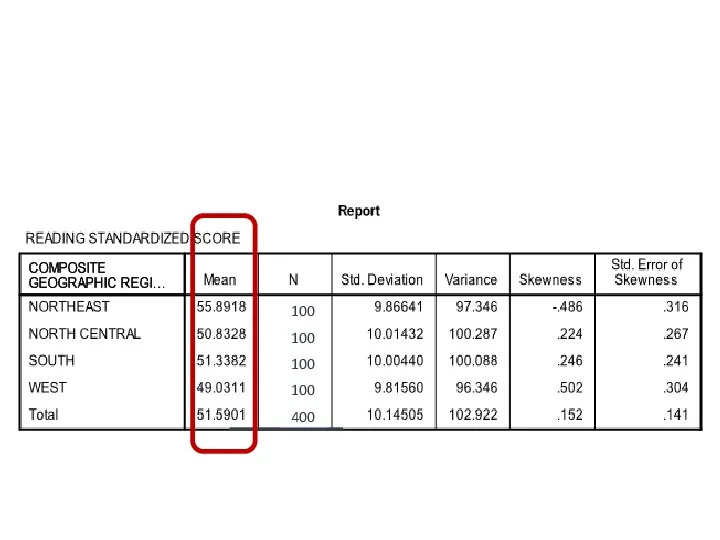
- 93. Exercise (16)
- 94. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 95. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 96. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 97. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 98. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 99. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 100. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
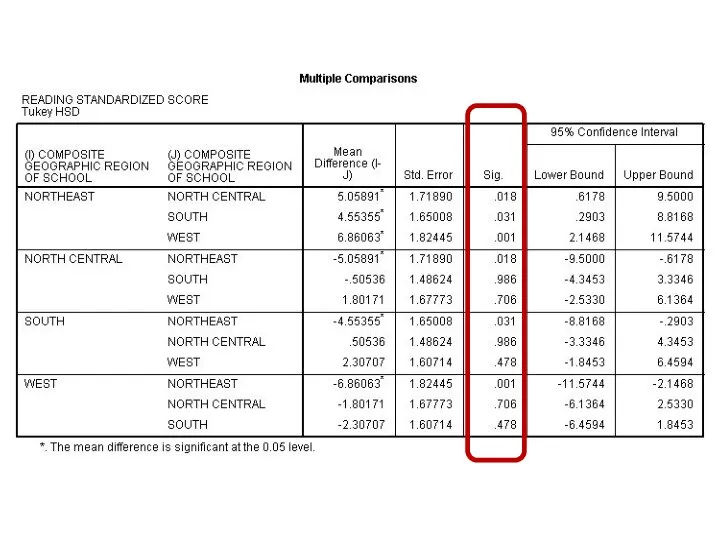
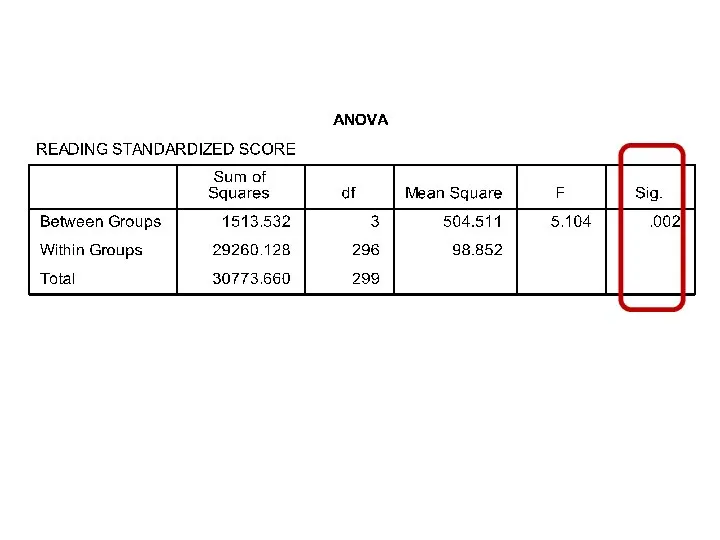
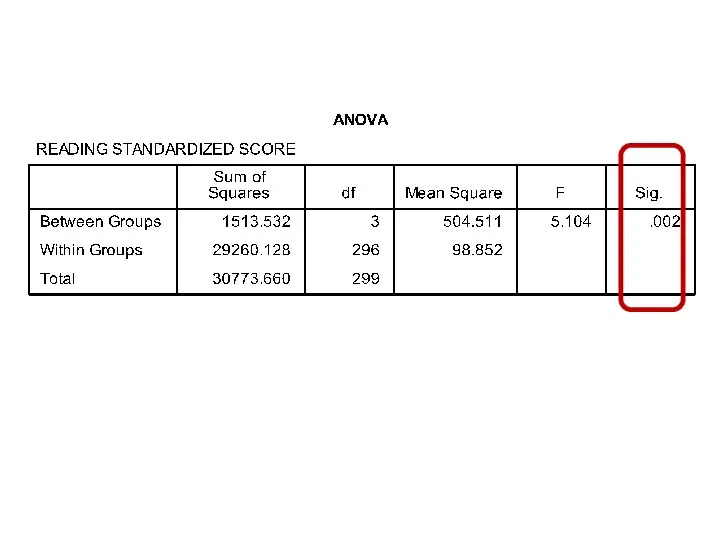
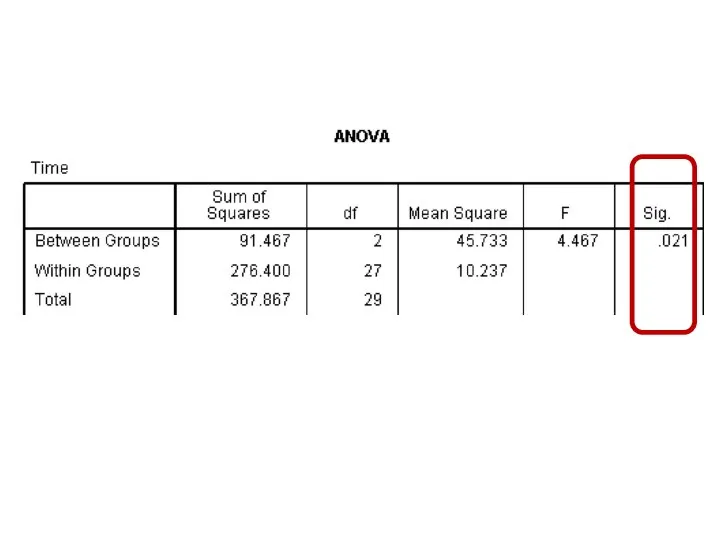
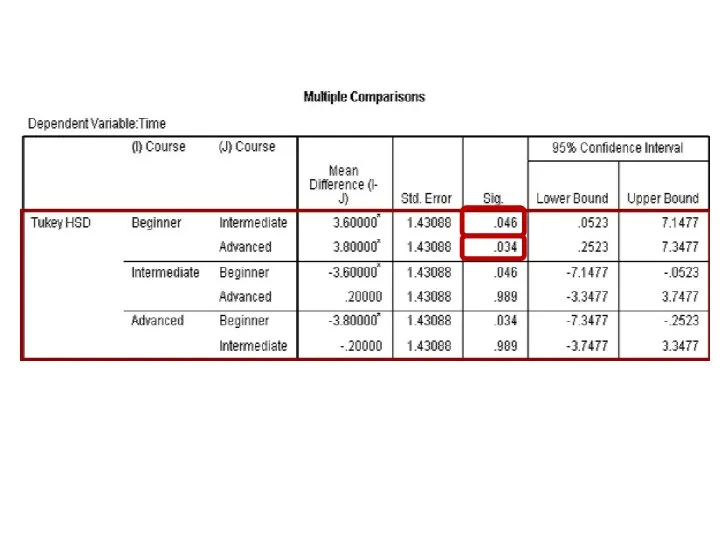
- 101. Exercise (17)
- 102. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 103. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 104. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 105. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 106. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 107. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 108. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 109. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 110. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 111. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 112. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 113. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
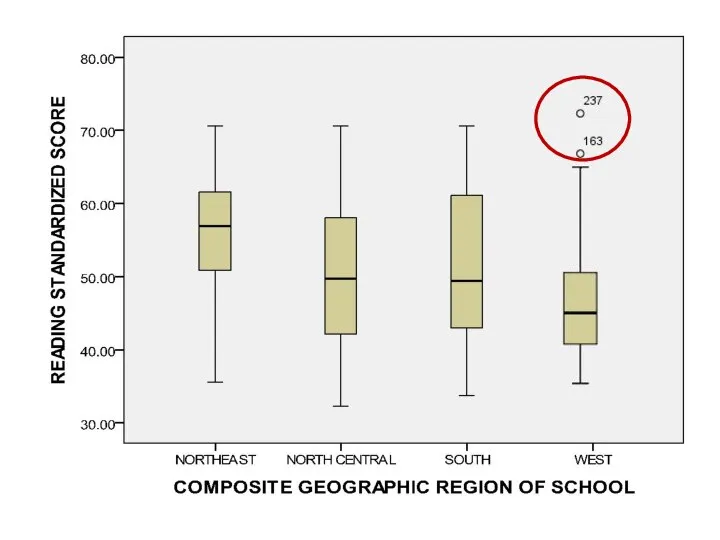
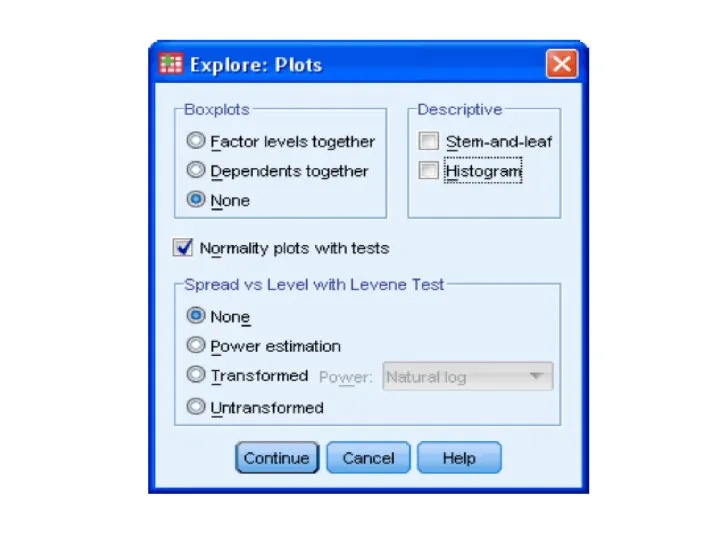
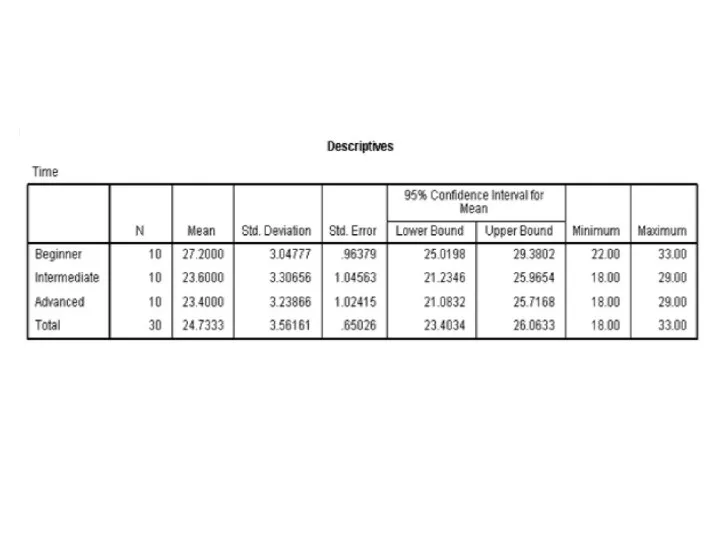
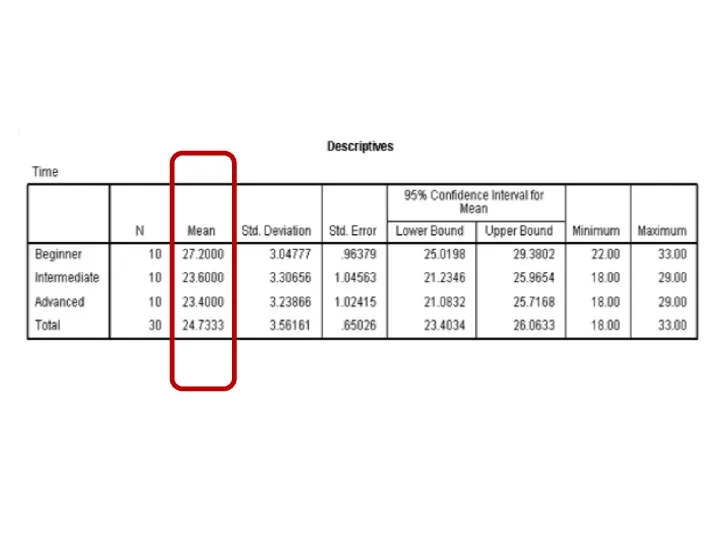
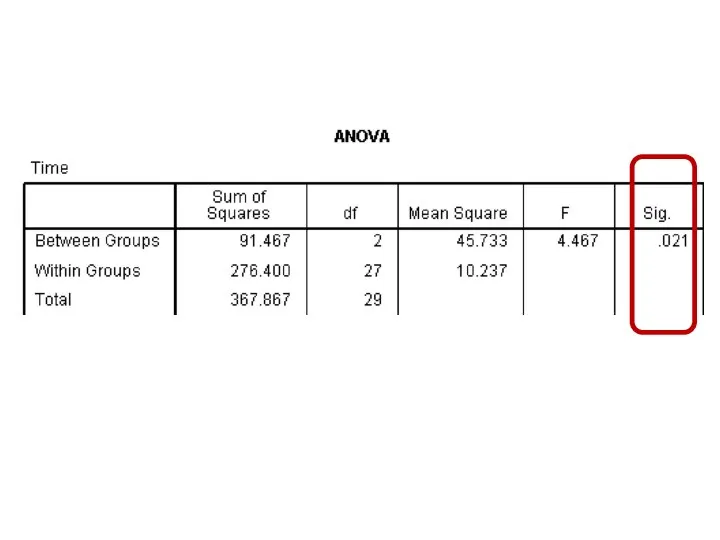
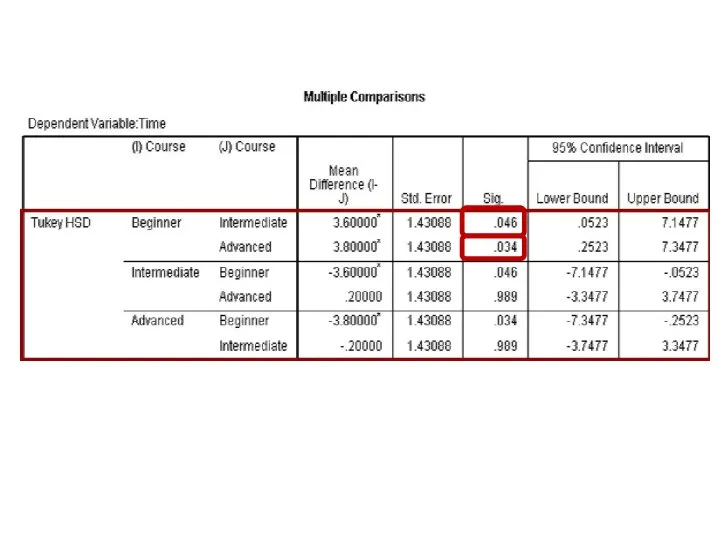
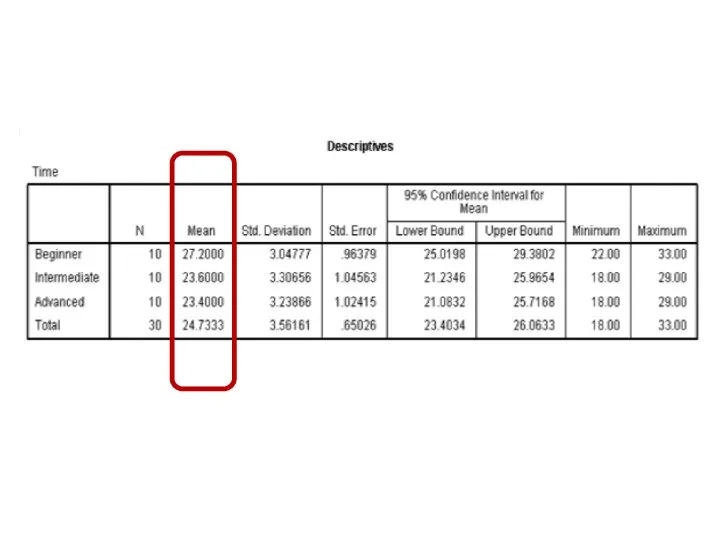
- 114. Box plot graph
- 116. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
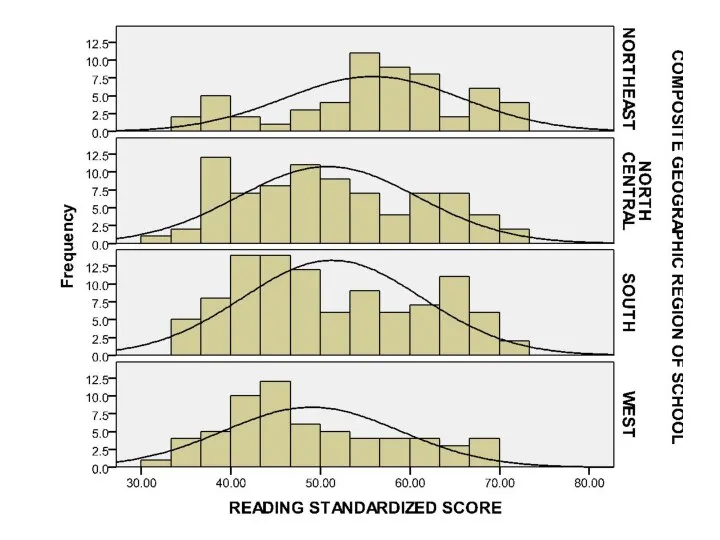
- 117. Histogram
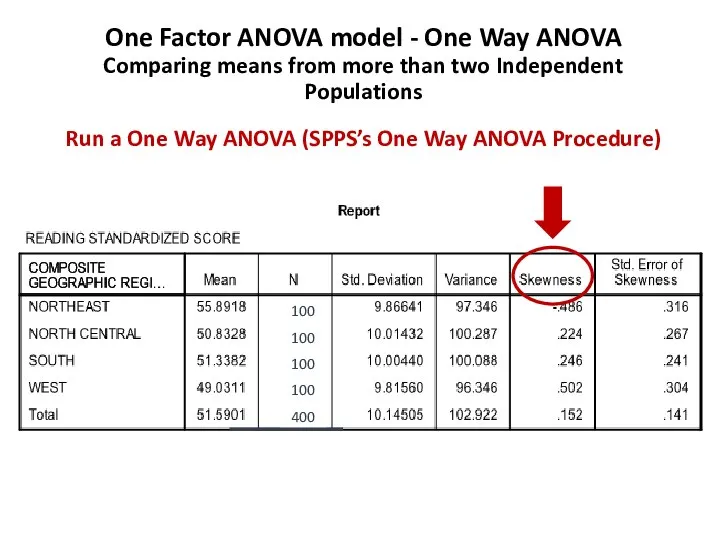
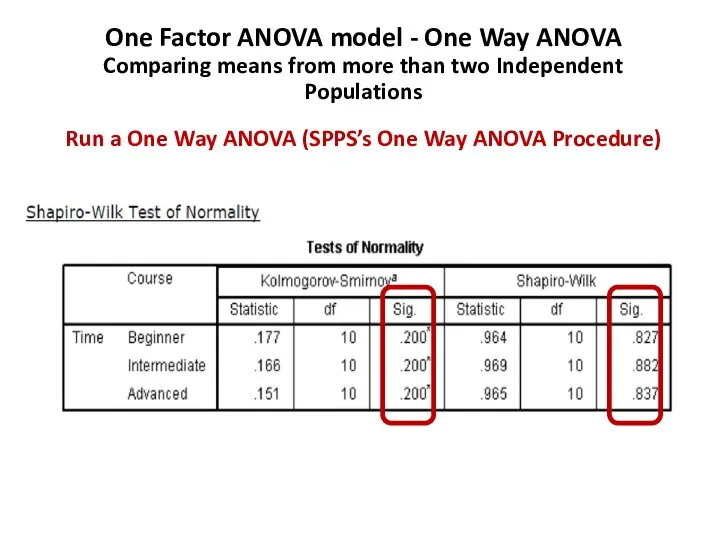
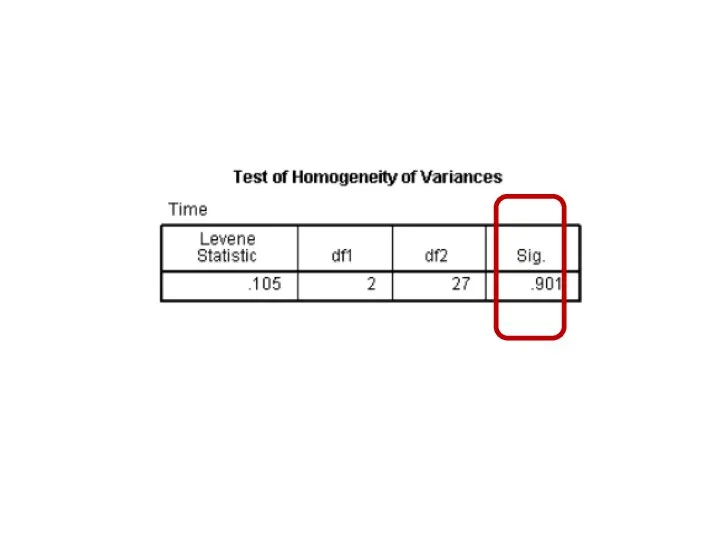
- 119. Tests of Normality
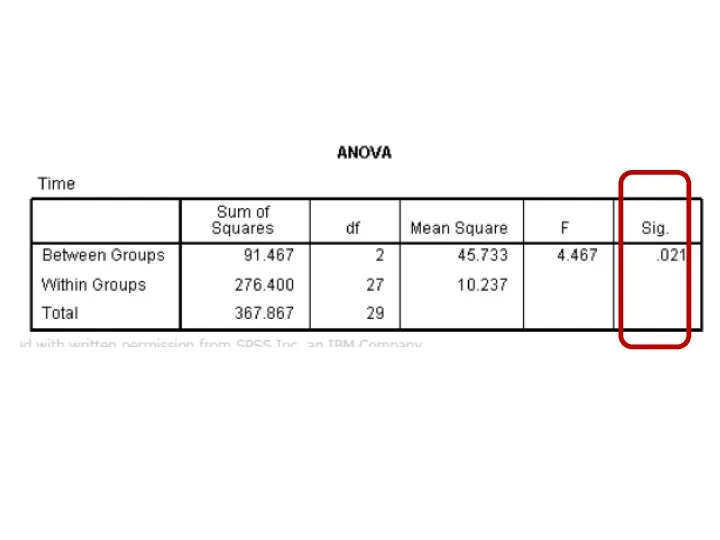
- 120. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 122. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 123. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
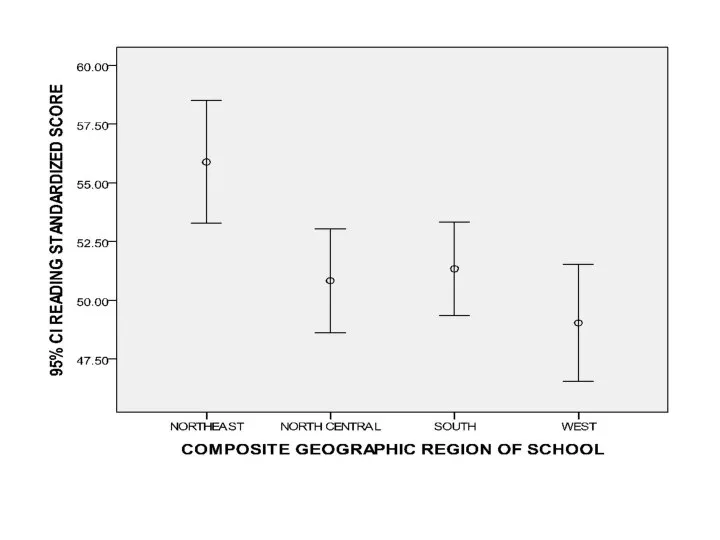
- 124. Error Bar graph
- 126. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 127. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 128. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
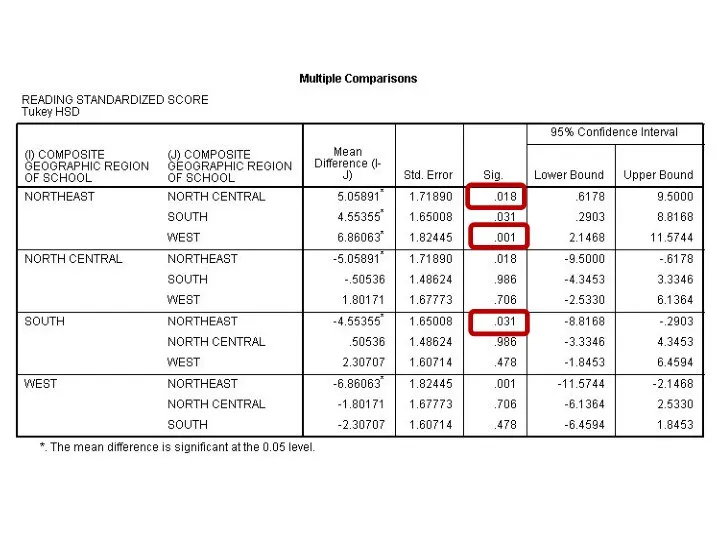
- 136. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 137. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 138. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 144. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 145. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 146. Return to Exercise (16)
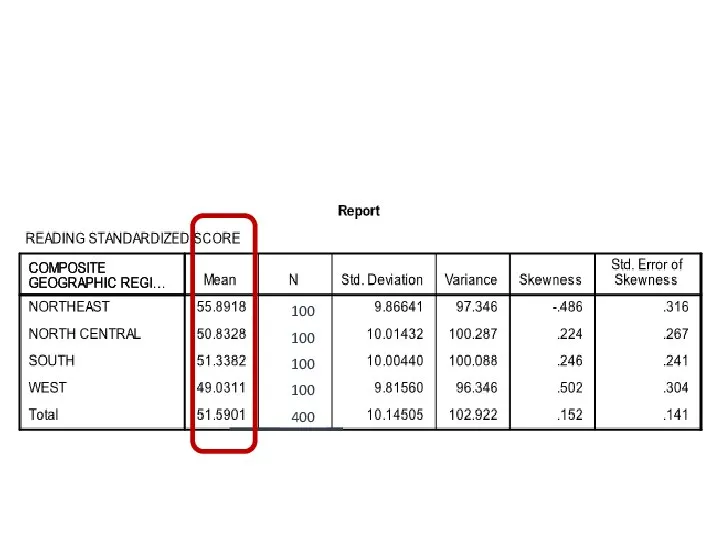
- 149. 100 100 100 100 400
- 150. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 152. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 153. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 155. 100 100 100 100 400
- 156. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
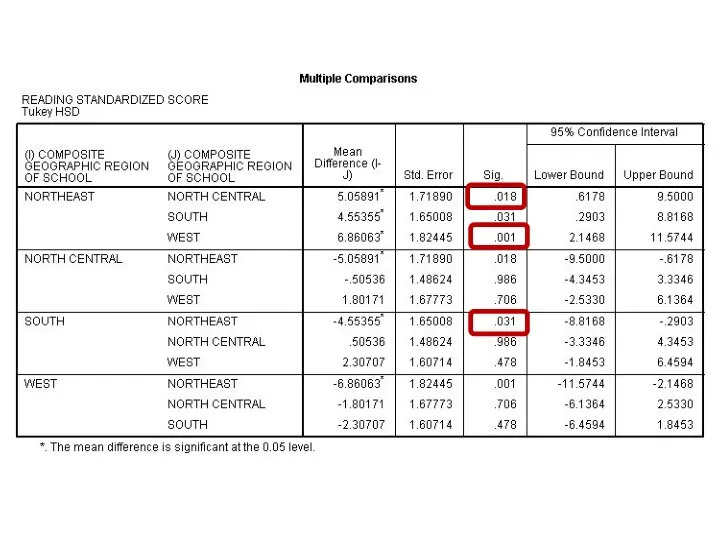
- 157. Return to Exercise (17)
- 161. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 163. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 164. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 167. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 168. One Factor ANOVA model - One Way ANOVA Comparing means from more than two Independent Populations
- 169. Comparing Means (Parametric tests) One Population Inference Two Population Inference Independent Sampling Model Dependent Sampling Model
- 172. Скачать презентацию









































































































 Врачевание в Древней Месопотамии
Врачевание в Древней Месопотамии На что способен наш мозг
На что способен наш мозг Биохимические показатели крови при различных клинических ситуациях
Биохимические показатели крови при различных клинических ситуациях Брюшной тиф
Брюшной тиф Простатит. Жалпы түсінік. Эпидемиологиясы
Простатит. Жалпы түсінік. Эпидемиологиясы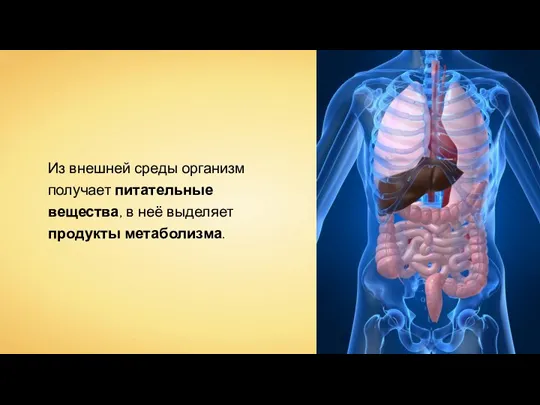 Продукты метаболизма
Продукты метаболизма Проктология, колопроктология
Проктология, колопроктология Аритмии и блокады
Аритмии и блокады Сердечно-сосудистая система
Сердечно-сосудистая система Клинический случай. Аллотрансплантация почки от живого родственного донора
Клинический случай. Аллотрансплантация почки от живого родственного донора Хроническая болезнь почек. Лабораторные анализы мочи
Хроническая болезнь почек. Лабораторные анализы мочи Мужские и женские молочные железы
Мужские и женские молочные железы Риккетсиозы. Морфология и биологические свойства. Клиническая картина. Диагностика. Профилактика
Риккетсиозы. Морфология и биологические свойства. Клиническая картина. Диагностика. Профилактика 695cbf6b-f690-48c9-acb3-4b1ee76b4469
695cbf6b-f690-48c9-acb3-4b1ee76b4469 Хирургические операции, классификация, характеристика
Хирургические операции, классификация, характеристика Методы обследования пациента в сестринской практике
Методы обследования пациента в сестринской практике Мазок на наличие бациллы Леффлера
Мазок на наличие бациллы Леффлера Душистые вещества. Гвоздика
Душистые вещества. Гвоздика Гипокальцемия у кошек
Гипокальцемия у кошек Подготовка документов для получения квоты на программу Вспомогательных Репродуктивных Технологий
Подготовка документов для получения квоты на программу Вспомогательных Репродуктивных Технологий Грип H1N1
Грип H1N1 Системная красная волчанка
Системная красная волчанка Анаэробные споронеобразующие бактерии
Анаэробные споронеобразующие бактерии Щитовидная железа
Щитовидная железа Питание детей 1-го года жизни. Организация питания на педиатрическом участке
Питание детей 1-го года жизни. Организация питания на педиатрическом участке Скелет свободной нижней конечности
Скелет свободной нижней конечности The first woman doctor in Russia
The first woman doctor in Russia Опухолевый процесс
Опухолевый процесс