Содержание
Слайд 31. Если функция непрерывна на отрезке, то она достигает на нем и
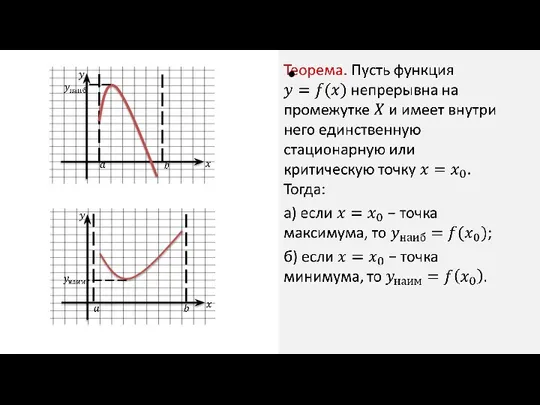
1. Если функция непрерывна на отрезке, то она достигает на нем и
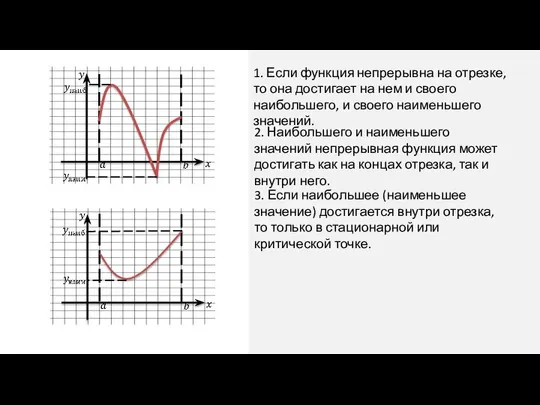
своего наибольшего, и своего наименьшего значений.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее (наименьшее значение) достигается внутри отрезка, то только в стационарной или критической точке.
Слайд 5Пример:
Пример:
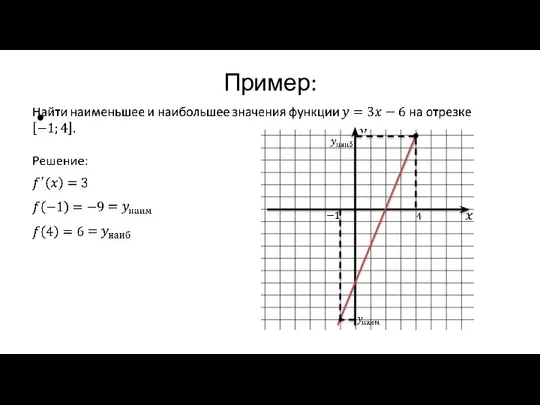
Слайд 6Пример:
Пример:
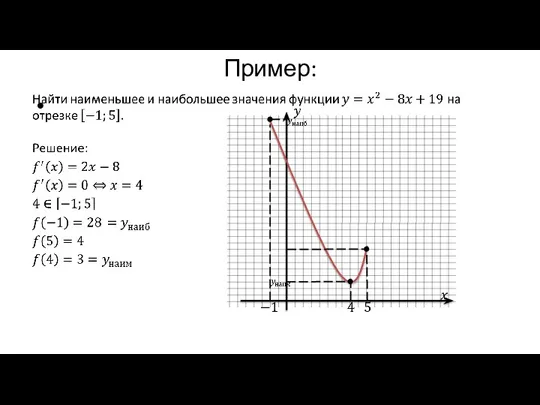
Слайд 8Пример:
Пример:
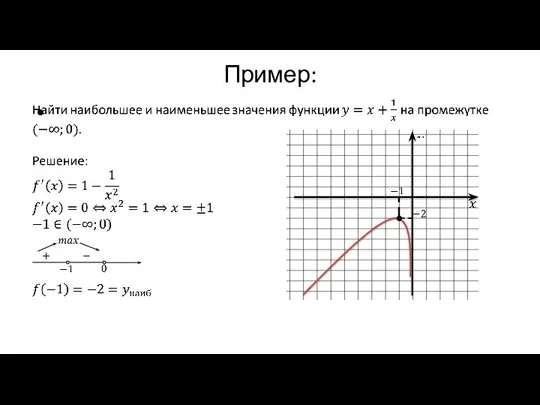
- Предыдущая
Притяжательные прилагательныеСледующая -
Знатоки дорожных знаков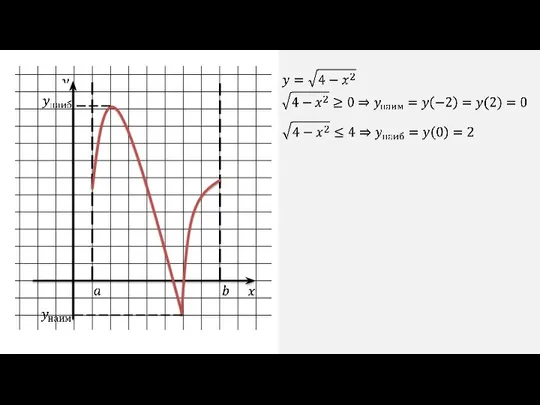

 Оценка острой кровопотери и гемотрансфузия при травме и синдроме ДВС
Оценка острой кровопотери и гемотрансфузия при травме и синдроме ДВС Индивидуальное здоровье человека
Индивидуальное здоровье человека trakheit_bronkhit
trakheit_bronkhit Психическое заболевание булимия
Психическое заболевание булимия Санитарно – эпидемиологический режим
Санитарно – эпидемиологический режим Понятие об электрическом поле источника тока. Однополюсные отведения. Отведения по Нэбу. Электрокардиограмма
Понятие об электрическом поле источника тока. Однополюсные отведения. Отведения по Нэбу. Электрокардиограмма Олигометастатическая болезнь при раке молочной железы
Олигометастатическая болезнь при раке молочной железы Рубец на матке. Перспективы самостоятельных родов
Рубец на матке. Перспективы самостоятельных родов Тест на ВИЧ: Экспедиция 2019
Тест на ВИЧ: Экспедиция 2019 Bronhopneumonia. Definiție
Bronhopneumonia. Definiție Правильное питание. 7 класс
Правильное питание. 7 класс Фракционный вакуумный массаж на аппарате ICOONE-H
Фракционный вакуумный массаж на аппарате ICOONE-H Гестационная трофобластическая болезнь
Гестационная трофобластическая болезнь Жіті сол қарыншалық жетіспеушілігінің диагностикасы және жедел жәрдем көрсету алгоритмі
Жіті сол қарыншалық жетіспеушілігінің диагностикасы және жедел жәрдем көрсету алгоритмі Паротит (свинка) у детей
Паротит (свинка) у детей Панариции и флегмоны кисти
Панариции и флегмоны кисти Синдром Леша-Нихана
Синдром Леша-Нихана Анализ заболевания почек
Анализ заболевания почек Суррогатты азық-түліктердің маңызы. Азық – түліктің фальсификациясы
Суррогатты азық-түліктердің маңызы. Азық – түліктің фальсификациясы Иммуноцитокины - цитокины
Иммуноцитокины - цитокины Неопиоидные анальгетики
Неопиоидные анальгетики Методы диагностики беременности и бесплодия
Методы диагностики беременности и бесплодия Внебольничная пневмония
Внебольничная пневмония Черепно-мозговые травмы. Переломы свода черепа. Переломы верхней и нижней челюсти. Переломы носа
Черепно-мозговые травмы. Переломы свода черепа. Переломы верхней и нижней челюсти. Переломы носа Экссудативный плеврит у детей
Экссудативный плеврит у детей Вены. Варикозная болезнь
Вены. Варикозная болезнь Wirus zapalenia wątroby typu B
Wirus zapalenia wątroby typu B Клиническая дерматология
Клиническая дерматология