Содержание
- 2. Эксперимент как метод исследований Эксперимент (от лат. «проба, опыт») - ведущий метод научного познания, направлен на
- 3. Виды переменных: Независимая переменная – это та, которую изменяет экспериментатор. Зависимая переменная – фактор, изменяющийся в
- 4. Основные этапы выполнения лабораторной работы:
- 5. Систематические погрешности обусловлены ограниченной точностью изготовления приборов (приборные погрешности), недостатками выбранного метода измерений, неточностью расчетной формулы,
- 6. Случайные погрешности вызываются большим числом случайных причин (изменением температуры, давления, сотрясения здания и т.д.), действия которых
- 7. Промахи, или грубые ошибки, - это неправильные отсчеты по прибору, неправильная запись отсчета и т.п. Как
- 8. Нахождение среднего значения и погрешности измерений методом границ (метод Корнфельда) В зависимости от характеристик измеряемой величины
- 9. Запись результатов измерений При вычислении абсолютной погрешности ∆x полученное значение округляют до одной значащей цифры. Сам
- 10. Прямые измерения Косвенные измерения Погрешности измерений 1) если единичное измерение 2) если несколько измерений: относительная погрешность:
- 11. L = (10.60 ± 0.05) см Приборная погрешность (интервал, в котором лежит истинное значение измеряемой величины
- 12. Запись и округление результата измерения 1) общий показатель степени выносят за скобку или заменяют соответствующей приставкой:
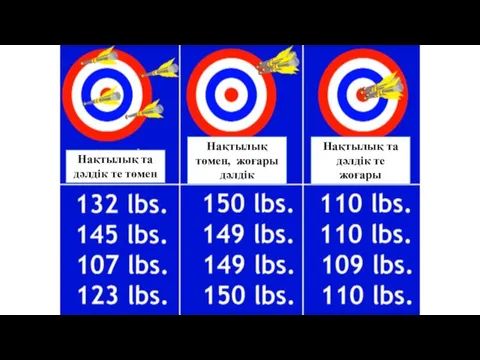
- 14. Нақтылық та дәлдік те төмен Нақтылық төмен, жоғары дәлдік Нақтылық та дәлдік те жоғары
- 15. Accuracy - a measure of how close a measurement is to the true value of the
- 16. Precision – a measure of how close a series of measurements are to one another. A
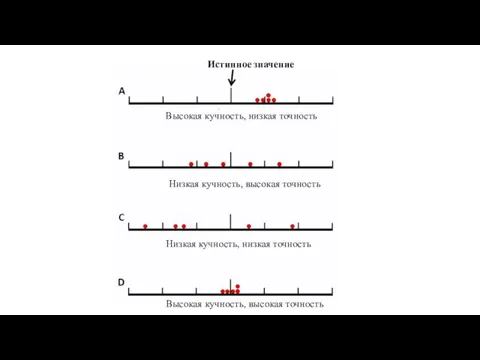
- 17. Истинное значение Высокая кучность, низкая точность Высокая кучность, высокая точность Низкая кучность, низкая точность Низкая кучность,
- 18. Example: Accuracy Who is more accurate when measuring a book that has a true length of
- 19. Example: Precision Who is more precise when measuring the same 17.0cm book? Susan: 17.0cm, 16.0cm, 18.0cm,
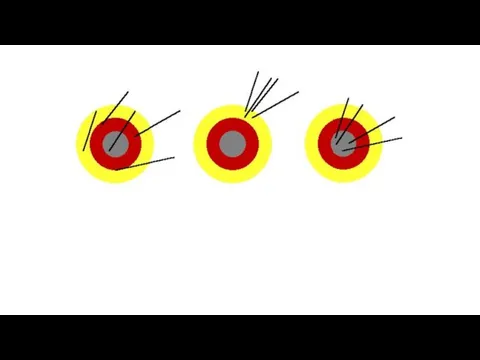
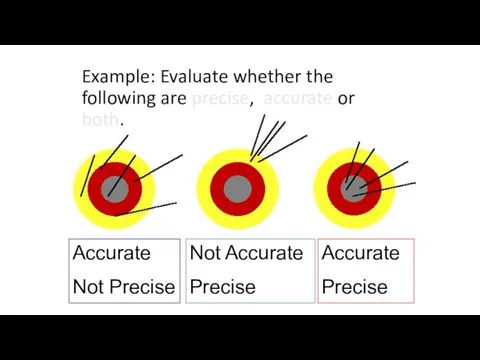
- 21. Example: Evaluate whether the following are precise, accurate or both. Accurate Not Precise Not Accurate Precise
- 22. Домашнее задание Четверо учеников измеряют длину карандаша линейкой. Фактический размер карандаша 15,0 см. Результаты измерений студентов
- 23. Представление данных: Первая строка таблицы (заголовок) должна быть заполнена (наименование физической величины /единица измерения); измерения следует
- 24. Оценка и управление рисками Риском называют вероятность возникновения какой-либо опасности во время проведения эксперимента. Под термином
- 25. If data are to be added or subtracted, add the absolute uncertainty: Propagating uncertainties through calculations
- 26. If data are to be multiplied or divided, add the fractional or percentage uncertainty: Propagating uncertainties
- 28. A 9.51 ± 0.15 meter rope ladder is hung from a roof that is 12.56 ±
- 29. A=(2.0+0.2)cm How to calculate the uncertainty of A square
- 30. A=(2.0+0.2)m How to calculate the uncertainty of square root of A*B? B=(4.0+0.1)m
- 32. Построение графиков Название графика, обозначение осей (физическая величина/единица измерения) Ось Ох - независимая переменная, Ось Оу-
- 33. При оформлении графического материала необходимо придерживаться следующих требований: -графики должны выполняться на миллиметровой бумаге; -по горизонтальной
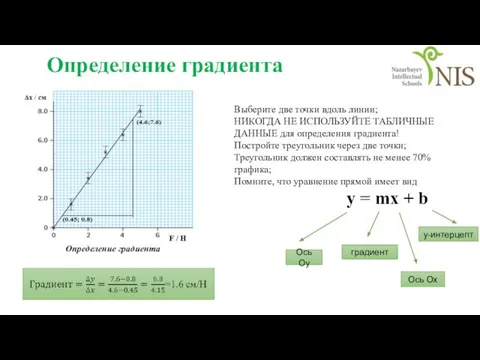
- 34. Определение градиента Ось Оу Ось Ох градиент у-интерцепт Определение градиента Выберите две точки вдоль линии; НИКОГДА
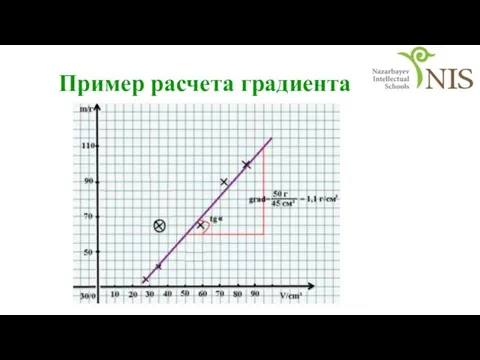
- 35. Пример расчета градиента
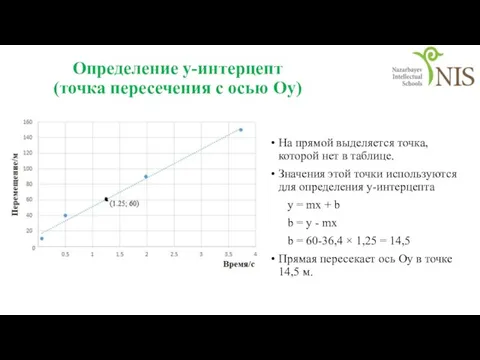
- 36. Определение у-интерцепт (точка пересечения с осью Оу) На прямой выделяется точка, которой нет в таблице. Значения
- 37. Линейная зависимость Задача нахождения наилучшей аппроксимирующей кривой в общем случае является достаточно сложной и наиболее просто
- 38. Практическая работа 2 «Приведение уравнения к линейной зависимости и построение графика»
- 39. Пересечение графика с осью ОУ (intercept) рано нулю.
- 40. 2. Результаты расчета дополнительных столбцов таблицы
- 42. Скачать презентацию
































 Дивногорский техникум лесных технологий
Дивногорский техникум лесных технологий Институт Аграрного Маркетинга
Институт Аграрного Маркетинга Введение. Что такое материал и материаловедение. Материалы природного происхождения
Введение. Что такое материал и материаловедение. Материалы природного происхождения Ссылки и их атрибуты Ссылки на документы и почтовые ссылки
Ссылки и их атрибуты Ссылки на документы и почтовые ссылки Спортивная подготовка в художественной гимнастике
Спортивная подготовка в художественной гимнастике Глава 3 Экономика фирмы
Глава 3 Экономика фирмы МАТЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ И КОНСТРУИРОВАНИЕ
МАТЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ И КОНСТРУИРОВАНИЕ Скинуло кафтан зелёный лето, Отсвистели жаворонки всласть, Осень в шубу жёлтую одета, По лесам с метёлкою прошлась. Раструбили жур
Скинуло кафтан зелёный лето, Отсвистели жаворонки всласть, Осень в шубу жёлтую одета, По лесам с метёлкою прошлась. Раструбили жур Rodina_Viktoria_Bi21-4_Chs_Tekhnogennogo_Kharaktera (1)
Rodina_Viktoria_Bi21-4_Chs_Tekhnogennogo_Kharaktera (1) История Русского церковного пения
История Русского церковного пения Виды слаймов
Виды слаймов Понятие и признаки налога. Принципы налогообложения. Налоговая система. Налоговое правоотношение
Понятие и признаки налога. Принципы налогообложения. Налоговая система. Налоговое правоотношение кибер-готы
кибер-готы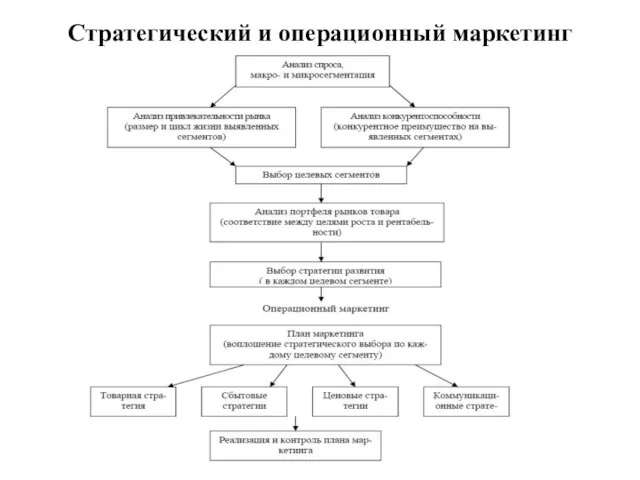 Стратегический и операционный маркетинг Детерминанты стратегического маркетинга
Стратегический и операционный маркетинг Детерминанты стратегического маркетинга Набор для обучения по программам подготовки сержантов запаса
Набор для обучения по программам подготовки сержантов запаса Куда пойти учиться в Амурской области
Куда пойти учиться в Амурской области Дети с тяжелыми нарушениями речи
Дети с тяжелыми нарушениями речи Основы бенчмаркинга (часть 2)
Основы бенчмаркинга (часть 2) pril
pril Термообработка с добавками (термодиффузионная обработка)
Термообработка с добавками (термодиффузионная обработка) Бальзам Уян Номо
Бальзам Уян Номо Strategy template. Шаблон
Strategy template. Шаблон 2CV – Rencontre mondiale
2CV – Rencontre mondiale Летняя образовательно-оздоровительная программа Хранители истоков
Летняя образовательно-оздоровительная программа Хранители истоков Презентация на тему ПРИНТЕРЫ
Презентация на тему ПРИНТЕРЫ  Презентация на тему Различные экосистемы
Презентация на тему Различные экосистемы  Поиск консультационной фирмы (консультанта). Тема 4
Поиск консультационной фирмы (консультанта). Тема 4 Создание лидирующих приложений
Создание лидирующих приложений