Содержание
- 2. Цели урока: Обобщить и систематизировать знания учащихся; Подготовиться к контрольной работе; Развить познавательный интерес учащихся к
- 3. В игре участвуют 4 команды. Каждая команда получает карточку, в которой указаны номера десяти вопросов. Учитель
- 4. Русское лото
- 5. 1 21 2 1 2 3 1 2 3 1 2 3 1 2 3 4
- 6. Что называют степенью числа a с натуральным показателем n ?
- 7. Как разделить степени с одинаковыми основаниями ?
- 8. Как возвести степень в степень ?
- 9. Как возвести в степень произведение ?
- 10. Что называется уравнением ?
- 11. Как возвести в степень дробь ?
- 12. Что, значит, решить уравнение ?
- 13. Что называется корнем уравнения ?
- 14. Что называется одночленом ?
- 15. Что называется многочленом ?
- 16. Какие одночлены называются подобными ?
- 17. Как привести подобные члены ?
- 18. Решите уравнение 2х+1=3х-х.
- 19. Представьте многочлен в стандартном виде
- 20. Решите уравнение (3х-9)(2х+1)=0.
- 21. Будет ли x = -3,071 корнем уравнения 8-20x = 45-16x-4x ?
- 22. Имеет ли смысл выражение
- 23. Приведите пример алгебраического выражения с переменной x, которое не имеет смысла при x=5.
- 24. Подберите такие значения a и b, чтобы выражение не имело смысла.
- 25. Как разделить многочлен на одночлен?
- 26. При каком значении m верно равенство ((x2)m)3=(x4)3(x3)2 ?
- 27. Упростить выражение
- 28. Вычислить 5x-1ּ 5xּ 53-2x.
- 29. Решите уравнение
- 30. Привести одночлен к стандартному виду (-5a3b2c)2ּac3.
- 31. Привести одночлен к стандартному виду –3x2ּxy2ּy3ּ(2- x)2.
- 32. Упростить выражение
- 33. Привести одночлен к стандартному виду
- 34. Сравнить два числа (-15)18 и (-18)15.
- 35. Найти ошибку (-7)(-7)(-7)(-7)=-74
- 36. Найти значение каждого из выражений
- 37. Найти значение выражения , при a= -2.
- 38. Будут ли данные одночлены подобными
- 39. Найдите значение многочлена при
- 40. Найти значение выражения (4+7a)-(3a+4) при a= -1,2.
- 41. Найти значение выражения (a2+b)-(a2-b) при a=1,7; b= -3.
- 42. Уравнения 2x-6=0; 3x+p=1 имеют общий корень. Найти pp.
- 43. Найти значение выражения при a=3.
- 44. Выполнить деление
- 45. Как умножить многочлен на многочлен?
- 46. Степенью числа а с натуральным показателем n , большим 1, называется произведение n множителей, каждый из
- 47. При деление степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются
- 48. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются
- 49. При возведении в степень произведения в эту степень возводится каждый множитель
- 50. Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением
- 51. При возведении в степень дроби в эту степень возводятся и числитель и знаменатель
- 52. Решить уравнение – это значит найти все его корни или установить, что их нет
- 53. Корнем уравнение называется то значение неизвестного, при котором это уравнение превращается в верное равенство
- 54. Произведение числовых и буквенных множителей называется одночленом
- 55. Многочленом называется алгебраическая сумма нескольких одночленов
- 56. Одночлены отличающиеся только коэффициентом называются подобными одночленами
- 57. Упрощение, при котором алгебраическая сумма подобных одночленов заменяется одним одночленом называется приведением подобных
- 58. 2х+1=3х-х 2х+1=2х 1=0 Ответ: Решений нет
- 60. (3х-9)(2х+1)=0 3х-9=0 2х+1=0 х=3 х= ½ Ответ: х=3, х=1/2
- 61. 8-20х =45-16х-4х 8 – 20х = 45 - 20х 8 ≠ 45 Ответ: корней нет х
- 62. нет
- 72. > 18 – четное число
- 73. (-7)(-7)(-7)(-7) =
- 74. ; ;
- 75. Будет ли х = - 3,071 являться корнем уравнения 8 – 20х =45 – 16х –
- 76. Подберите такие значения а и в, чтобы выражение не имело смысла
- 77. Что, значит, решить уравнение ?
- 78. Найти значение выражения при а = -2
- 79. При а = -2 получим 3∙(-8) – 6 = -24 –6 = - 30
- 80. да
- 81. При
- 82. (4+7a)-(3a+4)=4 + 7а – 3а – 4 =4а При а = - 1,2 получим 4 ∙(-
- 83. При а = 3 получим
- 84. 2x-6=0; 3x+p=1 х =3 3∙3 + р = 1 р = -8
- 85. (a2+b)-(a2-b)= 2b при a=1,7; b= -3 получим 2∙(-3) = -6
- 87. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена
- 88. Чтобы разделить многочлен на одночлен, нужно каждый член многочлена разделить на этот одночлен и полученные результаты
- 90. Скачать презентацию

























































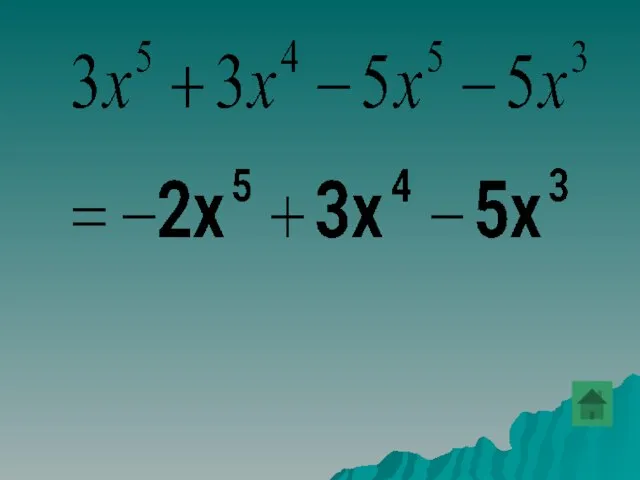



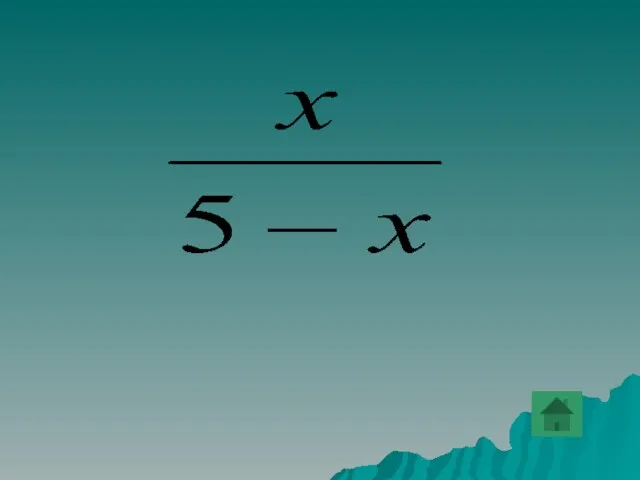
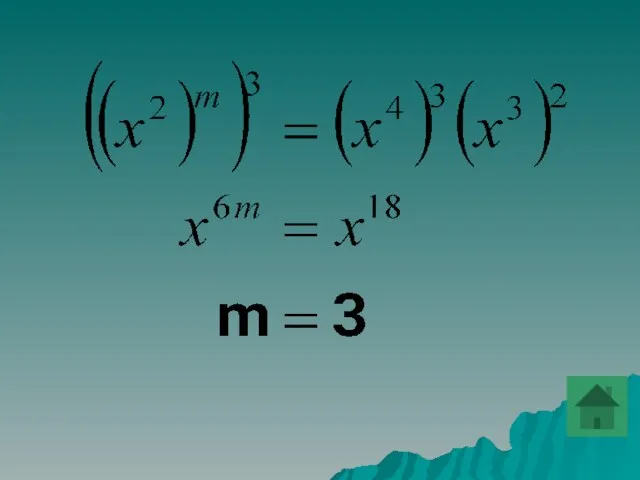
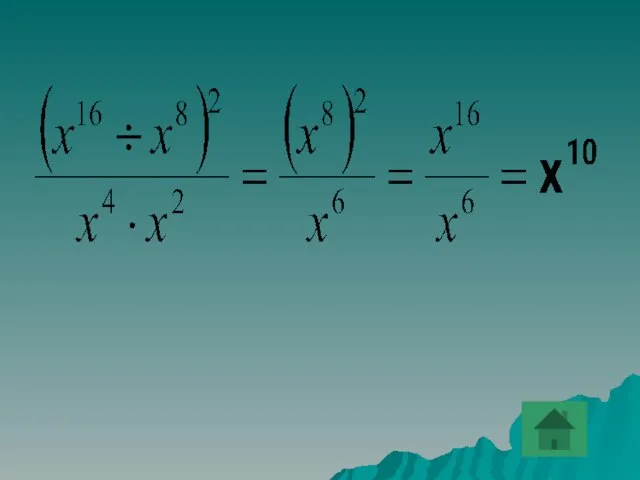
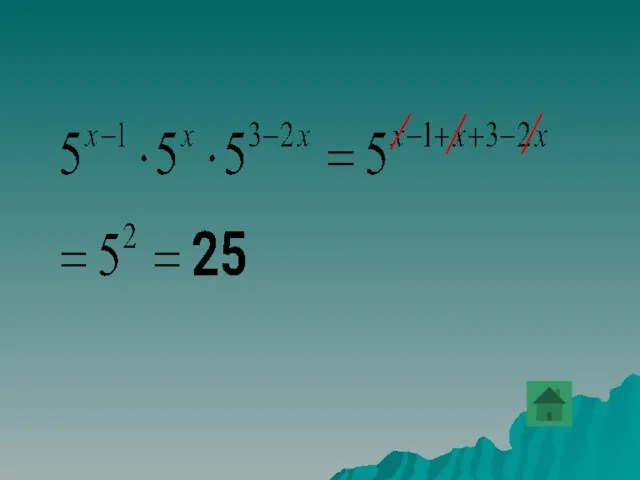
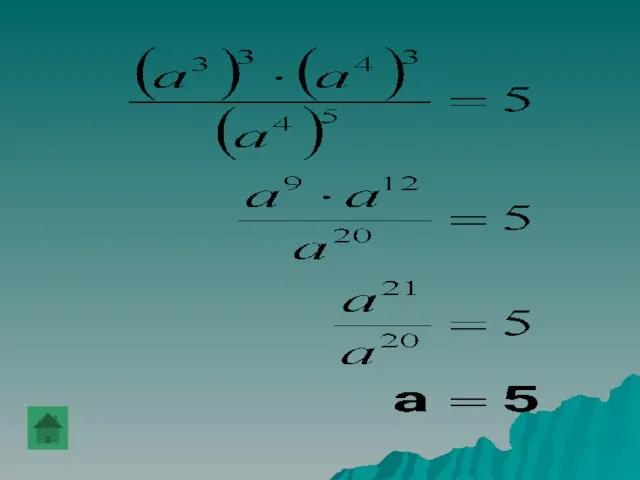
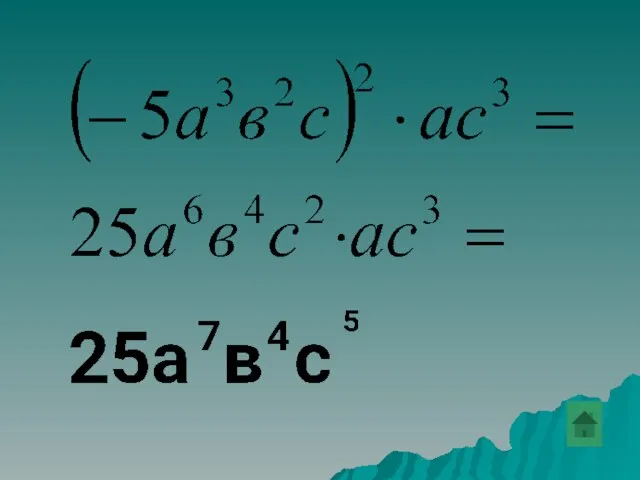
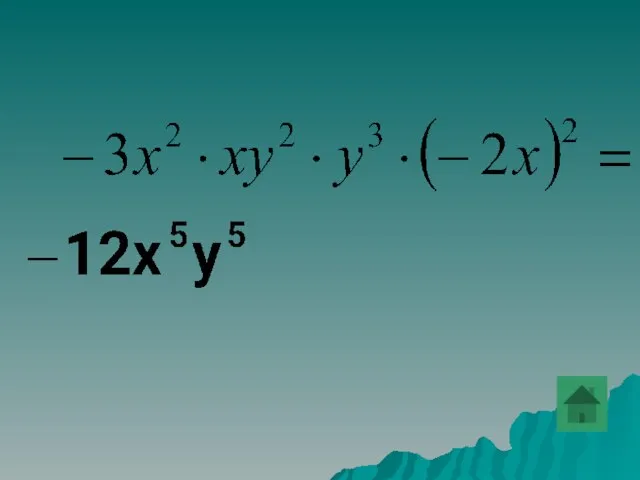
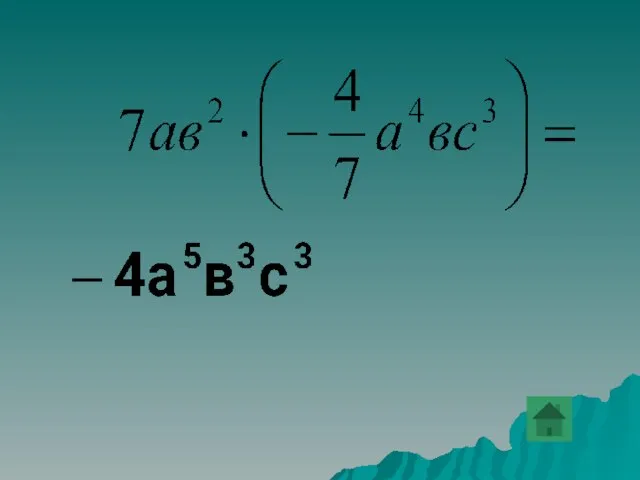
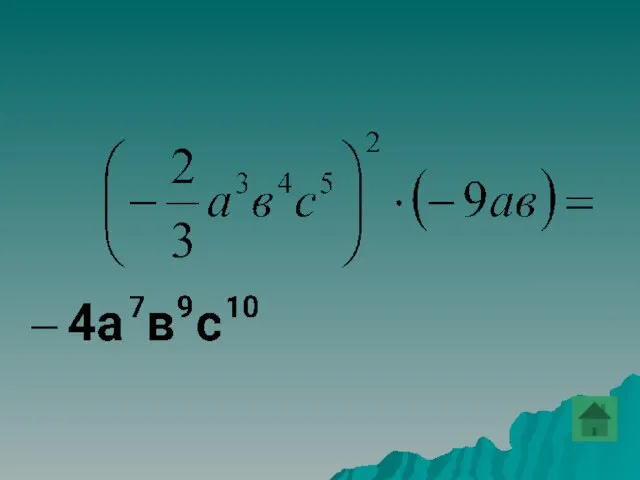
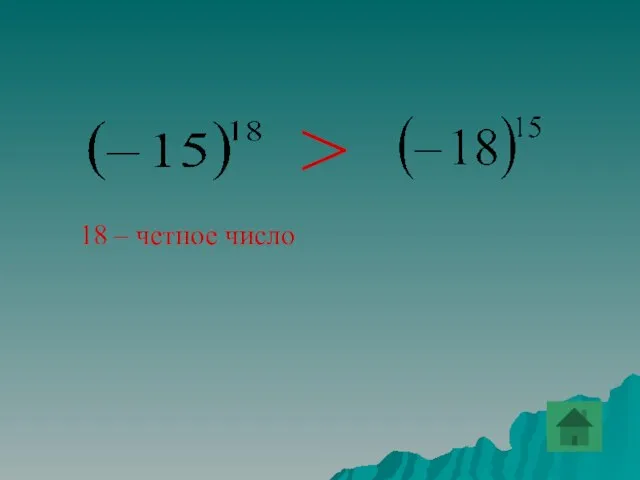
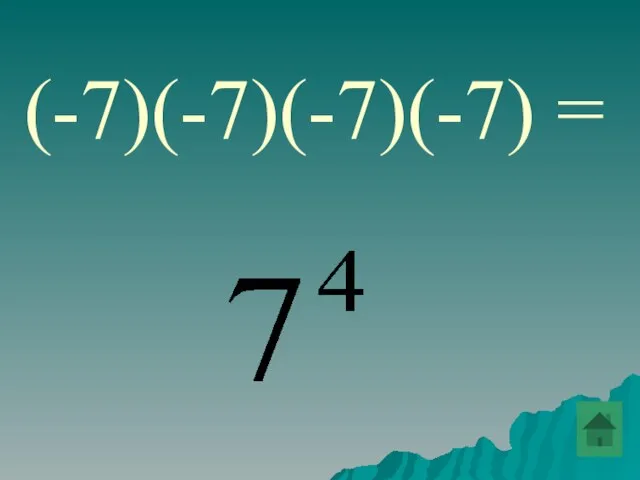
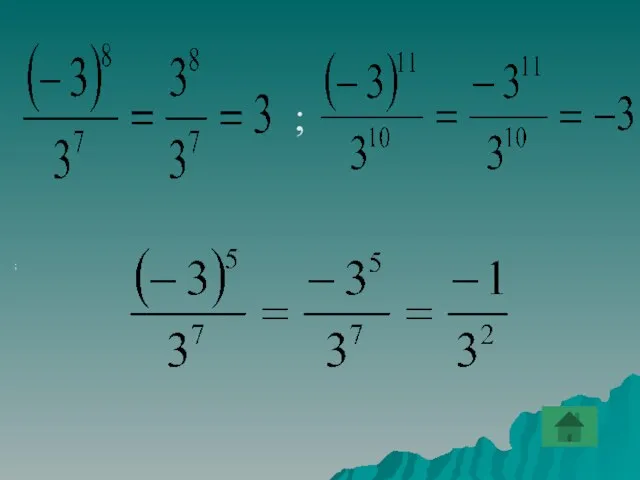




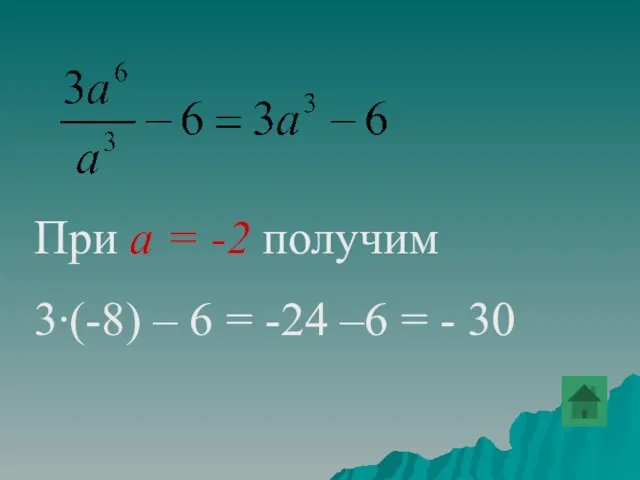
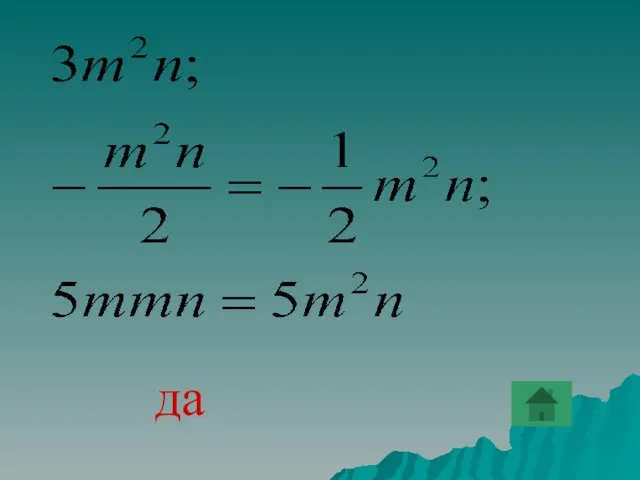
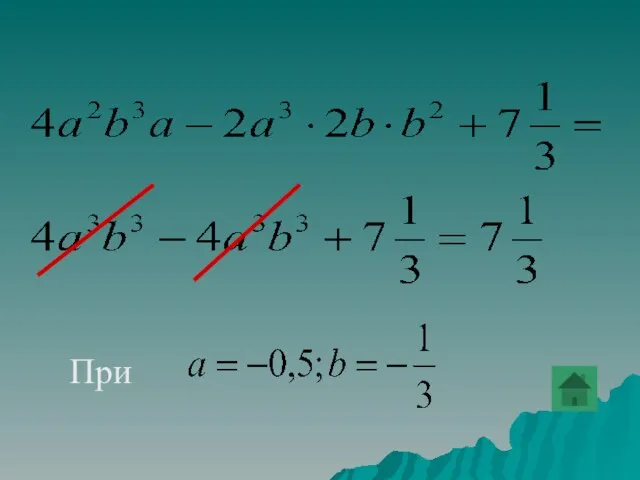

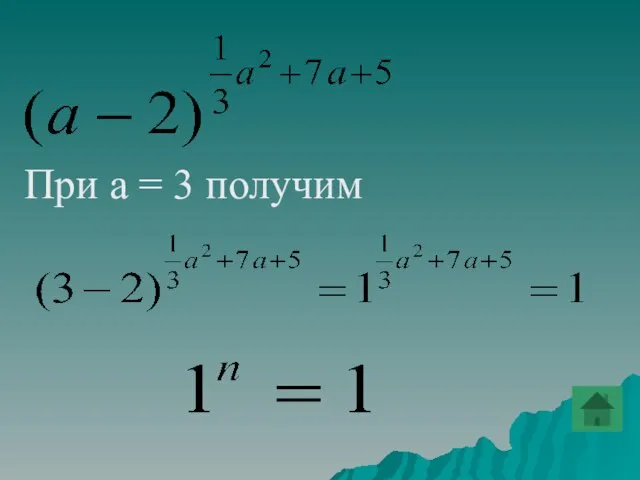
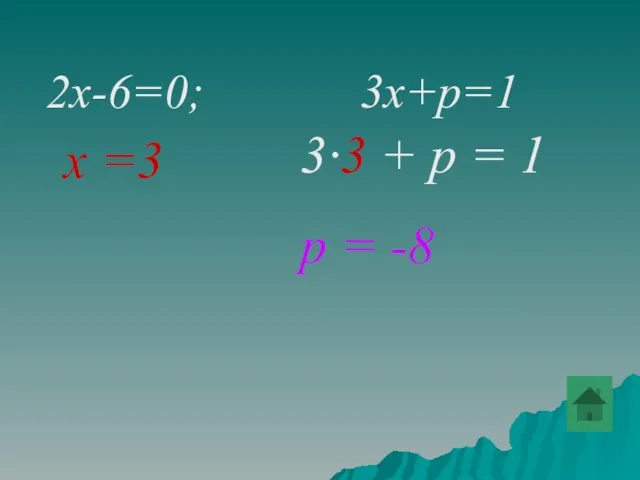

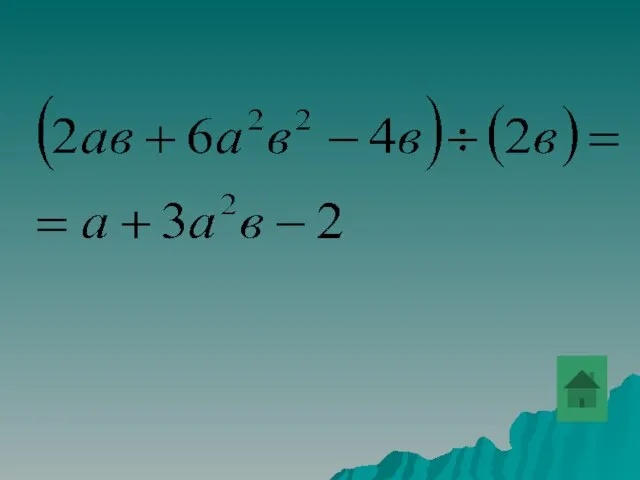


 Тема урока:Прикладная среда графического редактора Paint.
Тема урока:Прикладная среда графического редактора Paint. Презентация на тему Система национальных счетов
Презентация на тему Система национальных счетов Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр
Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр Cn(H2O)m
Cn(H2O)m 20140111_prezentatsiya_k_igre
20140111_prezentatsiya_k_igre Умей предупреждать болезни
Умей предупреждать болезни Еженедельное совещание. Статус работ блока Геология и разработка
Еженедельное совещание. Статус работ блока Геология и разработка Изделие Святой Николаус-Чудотворец
Изделие Святой Николаус-Чудотворец Среднее арифметическое, мода и размах ряда.
Среднее арифметическое, мода и размах ряда. Амплуа игроков в волейболе и их функции
Амплуа игроков в волейболе и их функции Страховые представители АО Страховая компания СОГАЗ-Мед
Страховые представители АО Страховая компания СОГАЗ-Мед «EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,
«EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,  Диего Веласкес. Сдача Бреды 1634–1635
Диего Веласкес. Сдача Бреды 1634–1635 К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается…
К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается… тема: «Воображение как общая способность»
тема: «Воображение как общая способность»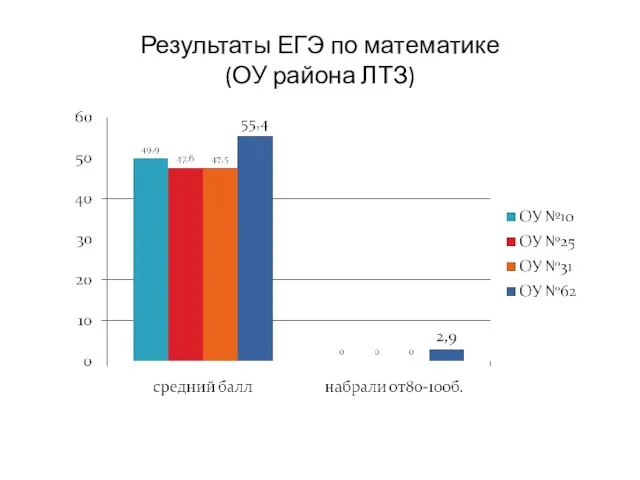 Результаты ЕГЭ по математике (ОУ района ЛТЗ)
Результаты ЕГЭ по математике (ОУ района ЛТЗ) Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина)
Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина) Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области
Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области ООО Глобал Контейнер Лоджистикс
ООО Глобал Контейнер Лоджистикс Жак Рене Ширак
Жак Рене Ширак Игра в слова
Игра в слова Бизнес-план Пончиковой
Бизнес-план Пончиковой Занятие 3 года обучения на каникулах. Декоративный натюрморт
Занятие 3 года обучения на каникулах. Декоративный натюрморт Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год
Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год Виды наказаний
Виды наказаний Ультразвуковой датчик
Ультразвуковой датчик Легенды театральной сцены
Легенды театральной сцены ПОДПИСКА
ПОДПИСКА