Содержание
- 2. Binary search
- 3. Binary search What does it mean for one element to be less than another?
- 4. Binary search What does mean sorting? Sorting means: to put into some well-defined order.
- 5. Binary search Binary search requires the array being searched to be already sorted.
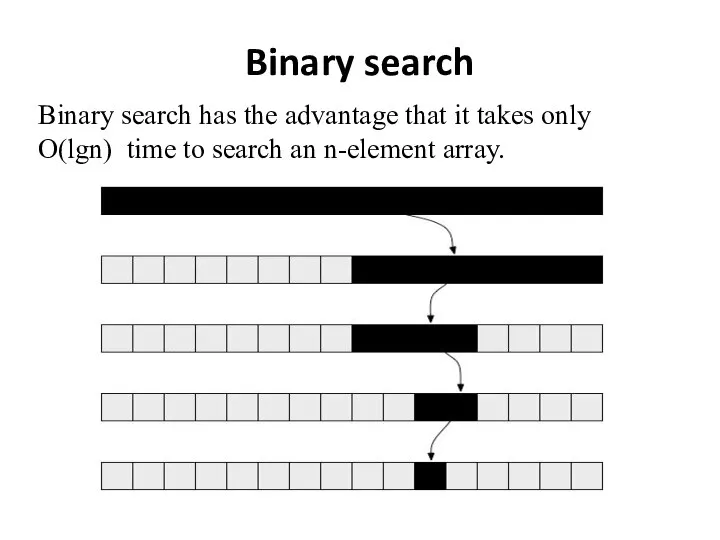
- 6. Binary search Binary search has the advantage that it takes only O(lgn) time to search an
- 7. Binary search The books on the bookshelf already sorted by author name. The position of the
- 8. Binary search
- 9. Binary search
- 10. Binary search The running time of binary search is O(lgn). ! The array is already sorted.
- 11. Selection sort Remind: Each element is less than or equals to its following element in the
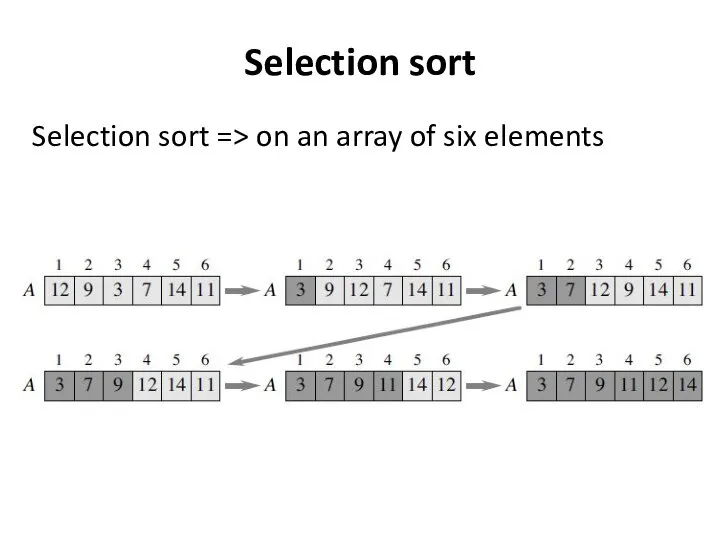
- 12. Selection sort Selection sort => on an array of six elements
- 13. Selection sort What is the running time of SELECTION-SORT?
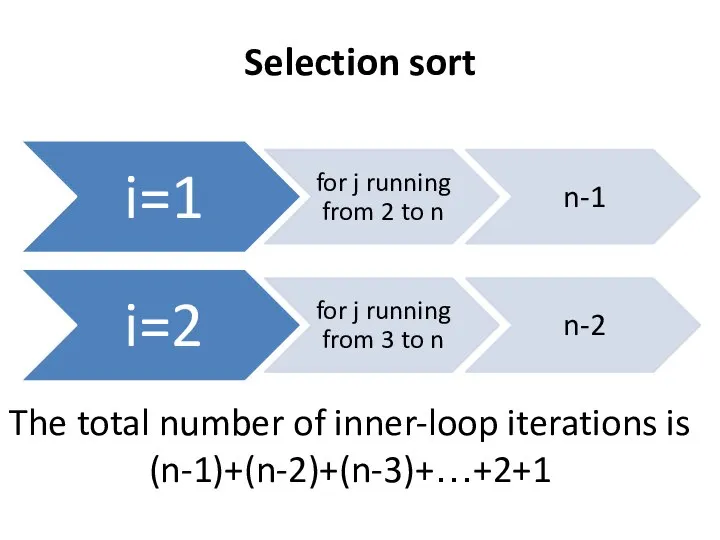
- 14. Selection sort The total number of inner-loop iterations is (n-1)+(n-2)+(n-3)+…+2+1
- 15. Selection sort n+(n-1)+(n-2)+(n-3)+…+2+1= =n(n+1)/2 It is sum of arithmetic series. (n-1)+(n-2)+(n-3)+…+2+1= =n(n-1)/2=(n2-n)/2
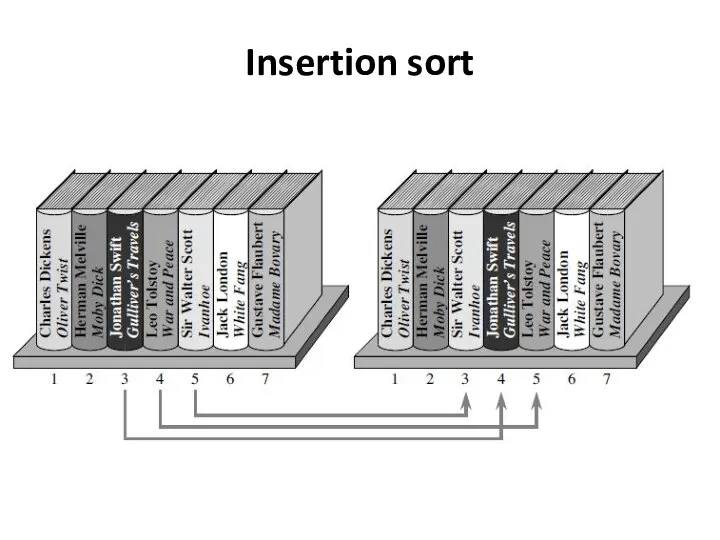
- 16. Insertion sort
- 17. Insertion sort
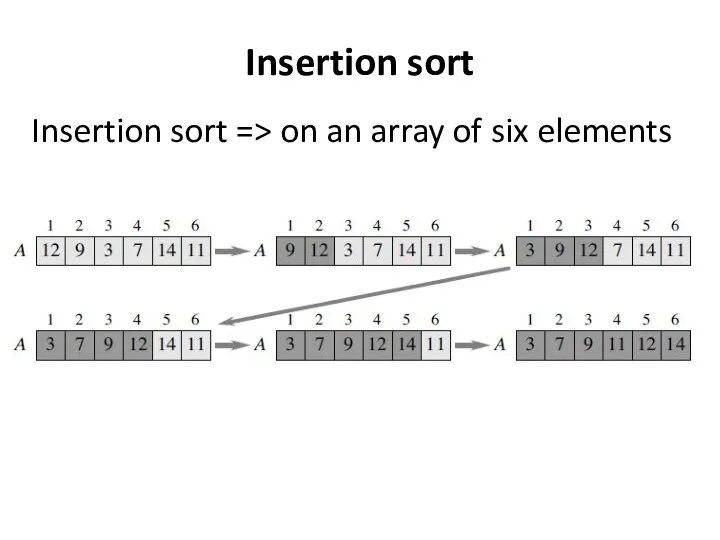
- 18. Insertion sort Insertion sort => on an array of six elements
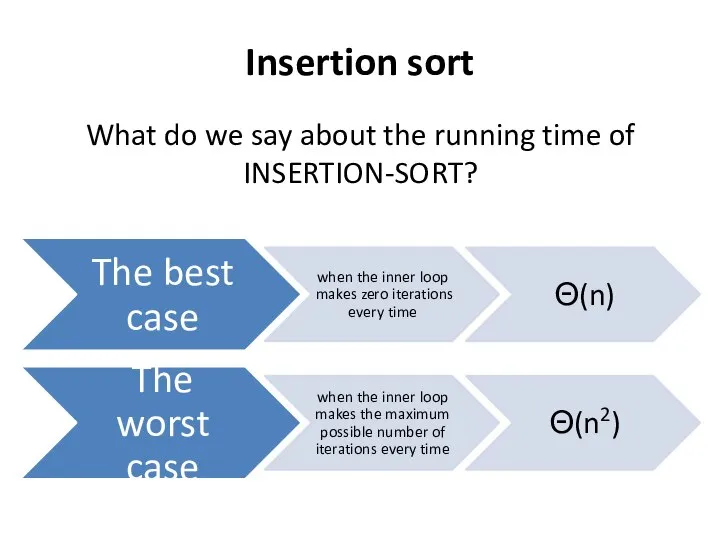
- 19. Insertion sort What do we say about the running time of INSERTION-SORT?
- 20. Merge sort The running times of selection sort and insertion sort are Θ(n2) . The running
- 21. Merge sort Disadvantages: The constant factor in the asymptotic notation is higher than for the other
- 22. Merge sort Divide-and-conquer algorithm Divide the problem into a number of subproblems that are smaller instances
- 23. Merge sort Divide all index (slot) of books in two part. The center of index’s books
- 24. Merge sort
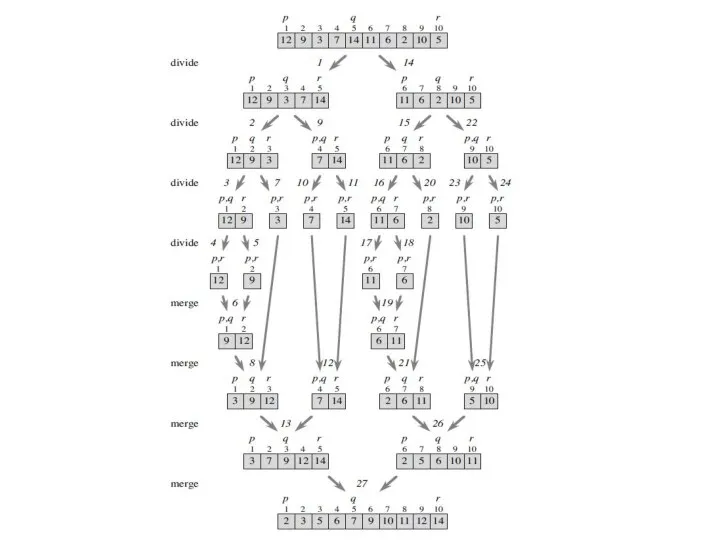
- 25. Merge sort The initial call is MERGE-SORT (A, 1, 10). Step 2A computes q to be
- 26. Merge sort At last, the call MERGE (A, 1, 5, 10) in step 2D The procedure
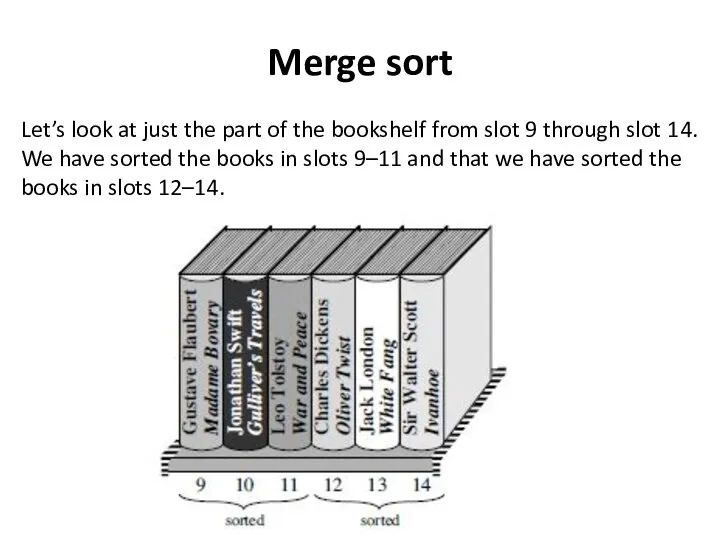
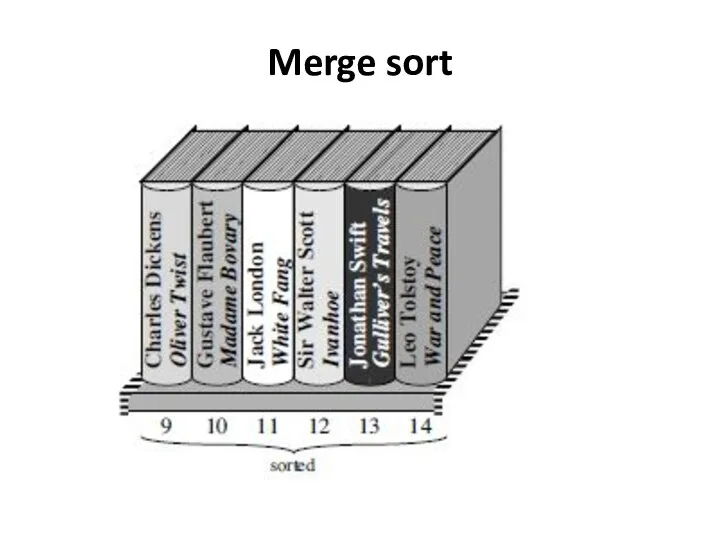
- 28. Merge sort Let’s look at just the part of the bookshelf from slot 9 through slot
- 29. Merge sort We take out the books in slots 9–11 and make a stack of them,
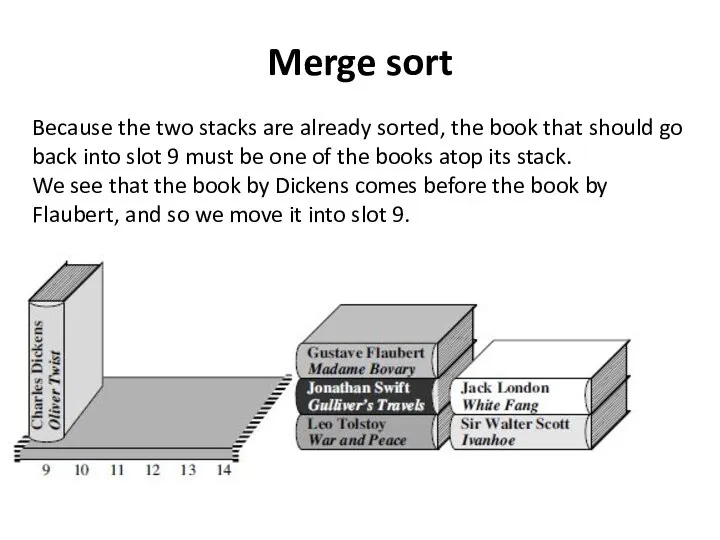
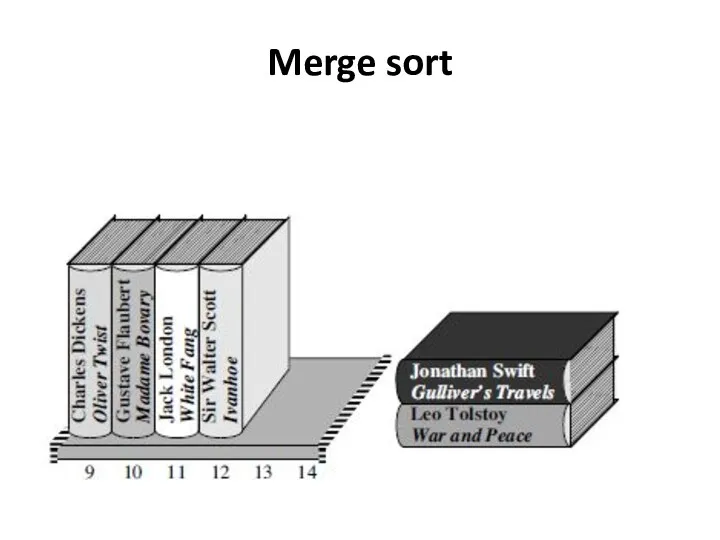
- 30. Merge sort Because the two stacks are already sorted, the book that should go back into
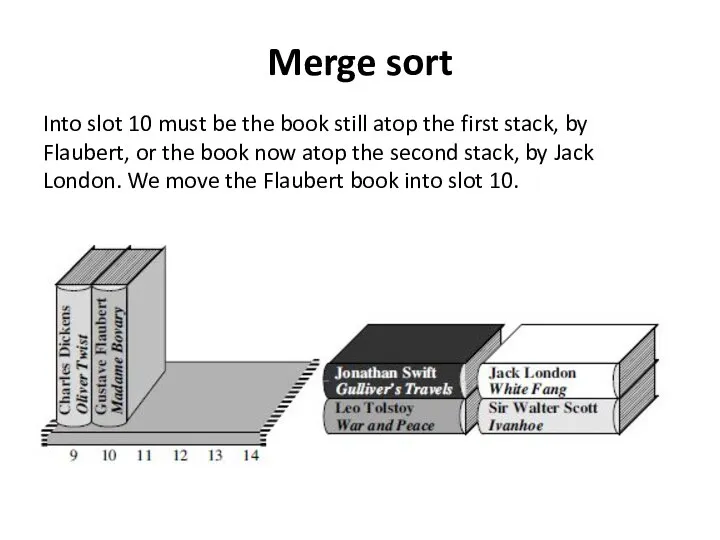
- 31. Merge sort Into slot 10 must be the book still atop the first stack, by Flaubert,
- 32. Merge sort
- 33. Merge sort
- 35. Merge sort Let’s say that sorting a subarray of n elements takes time T(n). The time
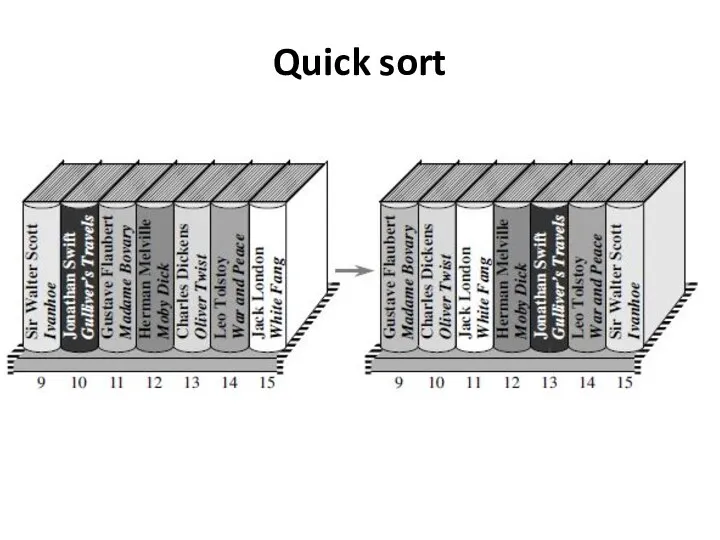
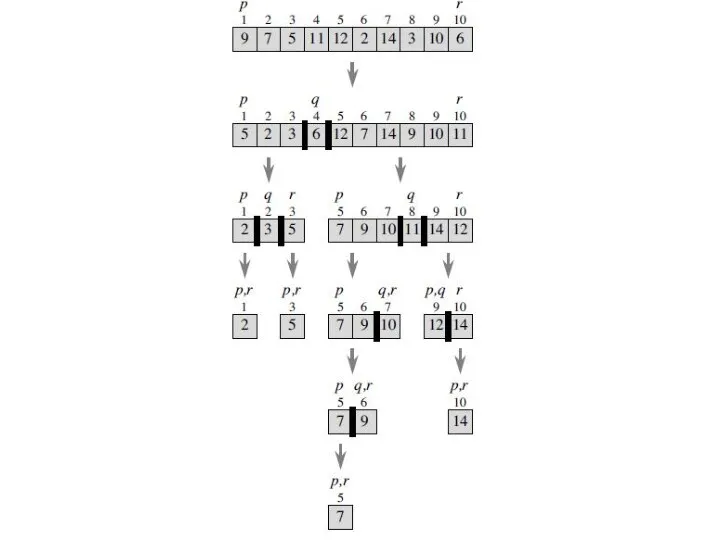
- 36. Quick sort Quicksort uses the divide-and-conquer paradigm and uses recursion. There are some differences from merge
- 37. Quick sort Divide by first choosing any one book that is in slots p through r.
- 38. Quick sort
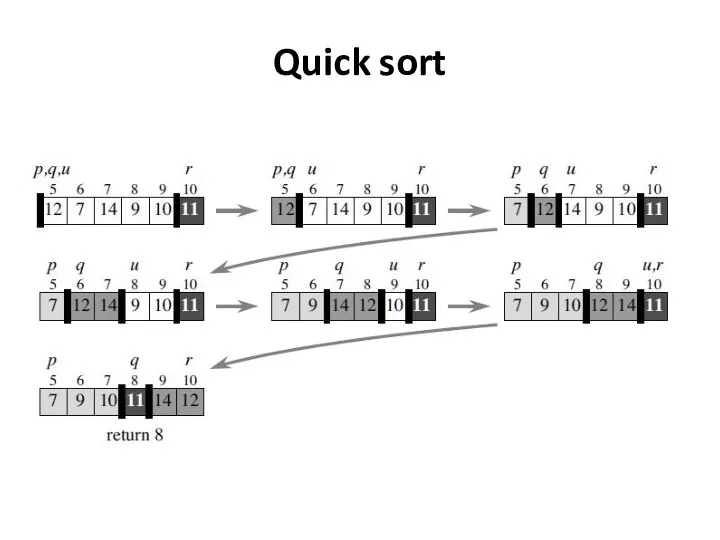
- 39. Quick sort The procedure PARTITION (A, p, r) that partitions the subarray A[p; r], returning the
- 41. Quick sort
- 42. Quick sort
- 43. Quick sort In better case quicksort has the running time Θ(nlgn). In the worst case quicksort
- 44. Recap
- 46. Скачать презентацию

























 Институциональное обеспечение стратегии развития муниципального образования
Институциональное обеспечение стратегии развития муниципального образования Традиционные украшения бурят
Традиционные украшения бурят Логика высказываний Алгоритм построения
Логика высказываний Алгоритм построения Всемирный день качества
Всемирный день качества РЕКЛАМНЫЕ ВОЗМОЖНОСТИ СЕТИ МАГАЗИНОВ МОЛОДЕЖНОЙ ОДЕЖДЫ ТВОЕ
РЕКЛАМНЫЕ ВОЗМОЖНОСТИ СЕТИ МАГАЗИНОВ МОЛОДЕЖНОЙ ОДЕЖДЫ ТВОЕ Имя существительное в русском и английском языках
Имя существительное в русском и английском языках Многофакторная модель интеллекта по Луису Терстоуну
Многофакторная модель интеллекта по Луису Терстоуну Избирательное право для всех и каждого
Избирательное право для всех и каждого Практическая работа по проектам Семейный клуб и Летние площадки психологической поддержки
Практическая работа по проектам Семейный клуб и Летние площадки психологической поддержки Британия, Британия, туманная страна…
Британия, Британия, туманная страна… Презентация на тему Виды международных договоров
Презентация на тему Виды международных договоров  MoBill – CAS(Control Access Service ) Учет использования услуг по магнитным картам
MoBill – CAS(Control Access Service ) Учет использования услуг по магнитным картам Номенклатура алканов разветвлённого строения
Номенклатура алканов разветвлённого строения Конституционно-правовой статус депутата Парламента Республики Казахстан. Тема 9
Конституционно-правовой статус депутата Парламента Республики Казахстан. Тема 9 Добро пожаловать!
Добро пожаловать! Предложения слушателей курсов ПК по результатам мониторинга Для совершенствования качества повышения квалификации слуша
Предложения слушателей курсов ПК по результатам мониторинга Для совершенствования качества повышения квалификации слуша Флора и фауна Мордовского края.
Флора и фауна Мордовского края. Концепция саморегулирования (Общие положения)
Концепция саморегулирования (Общие положения) Целеполагание в современных образовательных системах
Целеполагание в современных образовательных системах Методы и формы гражданского образования
Методы и формы гражданского образования Административное выдворение за пределы РФ. Дисквалификация
Административное выдворение за пределы РФ. Дисквалификация РУССКИЙ ЯЗЫК КАК ИНОСТРАННЫЙ Виртуальная выставка читального зала гуманитарных наук
РУССКИЙ ЯЗЫК КАК ИНОСТРАННЫЙ Виртуальная выставка читального зала гуманитарных наук «Внешнеэкономическая диспозиция России От ВТО до ЕЭП»
«Внешнеэкономическая диспозиция России От ВТО до ЕЭП» Шестое поколение мобильной связи
Шестое поколение мобильной связи Неделя карьеры ПАО КРИОГЕНМАШ
Неделя карьеры ПАО КРИОГЕНМАШ Презентация на тему Принтеры
Презентация на тему Принтеры Анне Андреевне Иващенко по случаю славного юбилея ОДА
Анне Андреевне Иващенко по случаю славного юбилея ОДА Виды общения
Виды общения