Содержание
- 2. Лекция 1. час 1. Введение. Содержание курса. 1.1. Цель и задачи курса. Определение понятия "физические свойства".
- 3. Цель и задачи курса Цель курса: Научить связывать физические свойства материалов с их структурой и фазовым
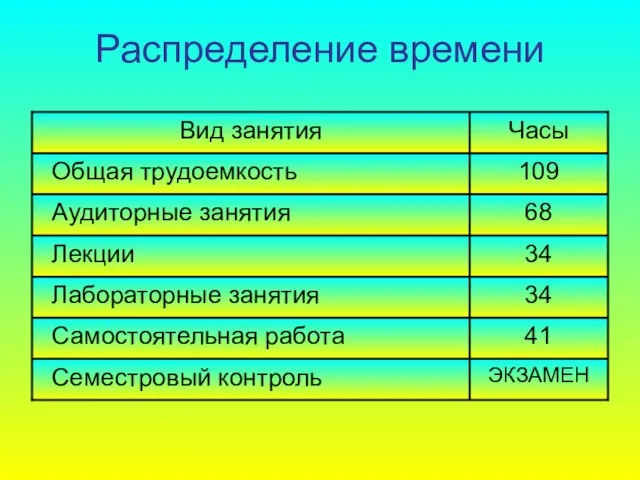
- 4. Распределение времени
- 5. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ Лекции – 34 ч 6 Лабораторных работ – 34 ч Самостоятельная работа –
- 6. Программа курса Тема 1. Введение (1 час) Тема 2. Тепловые свойства (теплоемкость и энтальпия), термическое расширение,
- 7. Литература Лившиц Б.Г., Крапошин В.С., Линецкий Я.Л. Физические свойства металлов и сплавов. М.: Металлургия, 1980, 318
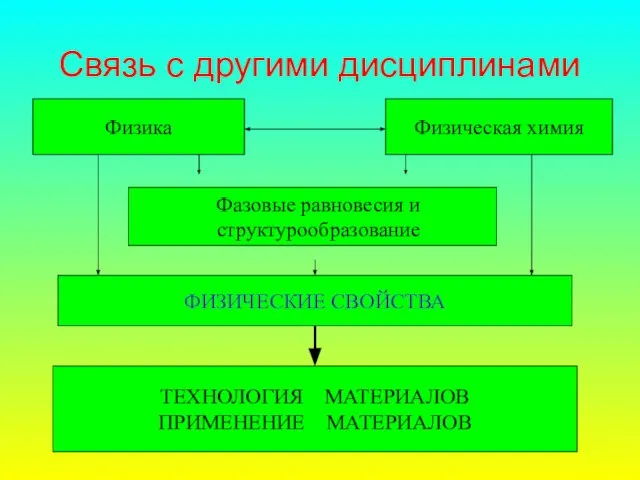
- 8. Связь с другими дисциплинами Физика Физическая химия Фазовые равновесия и структурообразование ФИЗИЧЕСКИЕ СВОЙСТВА ТЕХНОЛОГИЯ МАТЕРИАЛОВ ПРИМЕНЕНИЕ
- 9. Классификация физических свойств по влиянию микроструктуры и дефектов кристаллической решетки: 1. структурно-чувствительные свойства (ρ, λ, μ,
- 10. Влияние обработки на свойства стали У8 Отжиг Сфероидизирующий Закалка отжиг Bs=2,1 Тл Вs=2,1 Тл Вs=1,8 Тл
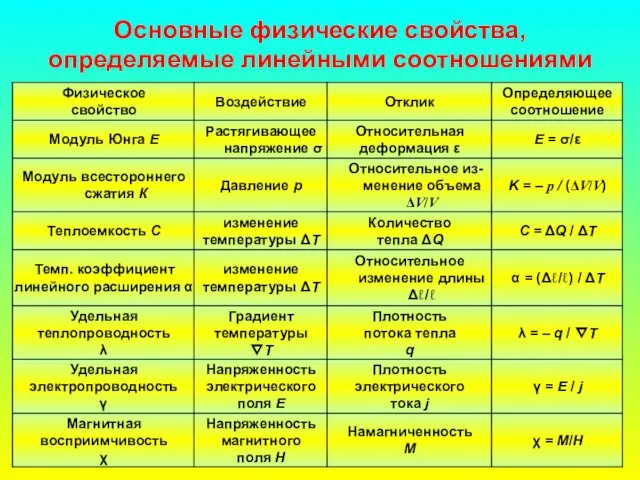
- 11. Классификация по виду физического эффекта Физический эффект, «порождающий» физическое свойство, может быть охарактеризован путем описания воздействия
- 12. Основные физические свойства, определяемые линейными соотношениями
- 13. Комментарии Различие между воздействием и откликом иногда довольно условно. Под воздействием понимают физическую величину, значение которой
- 14. Некоторые особенности физических свойств наноматериалов. В наноструктурных материалах часто изменяются фундаментальные характеристики, такие как Точка Кюри,
- 15. Лекция 2. час 2. Тема 1. Тепловые свойства. 1. Общие понятия и определения (энтальпия, виды теплоемкости
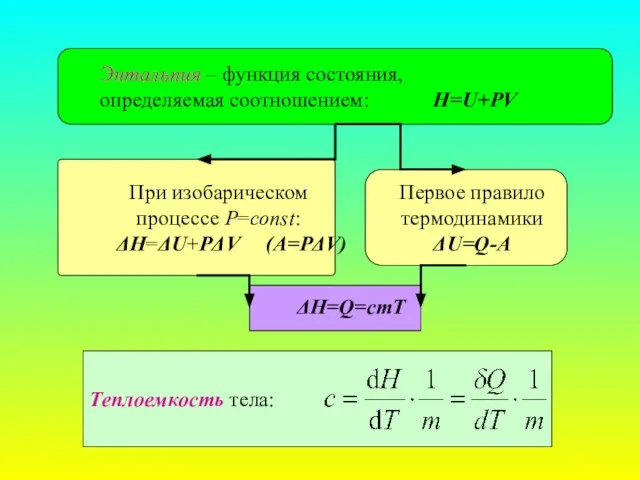
- 16. Энтальпия – функция состояния, определяемая соотношением: H=U+PV При изобарическом процессе P=const: ΔH=ΔU+PΔV (A=PΔV) Первое правило термодинамики
- 17. Виды теплоемкости Теплоемкость тела: C = δQ/dT [Дж/К]. Удельная теплоемкость: Суд = С/m [Дж/кг·К]. Молярная теплоемкость:
- 18. Теплоемкость для разных условий передачи тепла Теплоемкость при постоянном объеме: CV = (∂U/∂T)V=const. Теплоемкость при постоянном
- 19. Различие теплоемкостей Объемный коэффициент термического расширения Коэффициент всестороннего сжатия (сжимаемость)
- 20. Формула Нернста-Линдемана Причем a≠f(T) Для металлов ΔС очень мала: СP ≈ CV . (1+10-4T), НО Для
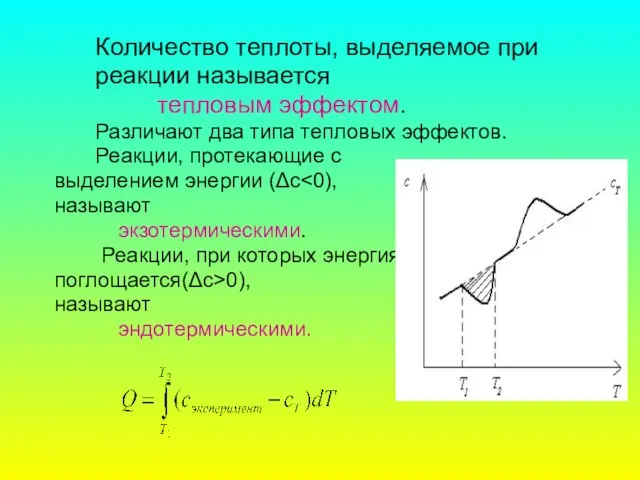
- 21. Количество теплоты, выделяемое при реакции называется тепловым эффектом. Различают два типа тепловых эффектов. Реакции, протекающие с
- 22. Составляющие теплоемкости Cp = Cрешетки + Сэл = = Сидеальной решетки + Сдефект + Сэл =
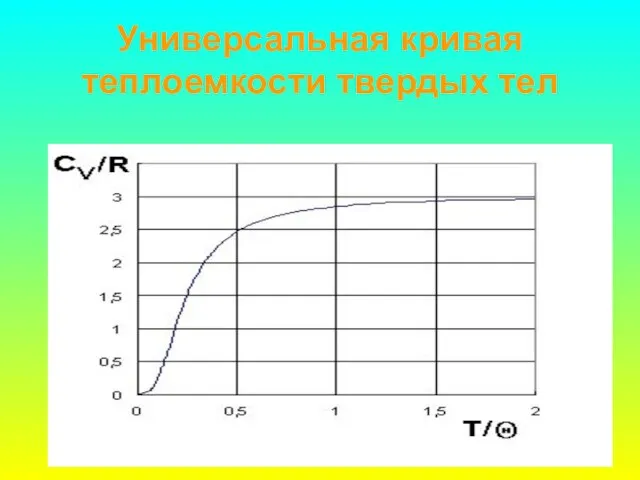
- 23. Универсальная кривая теплоемкости твердых тел
- 24. Решеточная теплоемкость 1 классическое приближение Средняя энергия классического осциллятора на 1 степень свободы: на 3 степени
- 25. Решеточная теплоемкость 2 классическое приближение Всего 6 степеней свободы – 3 - поступательное движение 3 -
- 26. Лекция 2. 2. Теории теплоемкости Эйнштейна и Дебая. Дебаевская температура как характеристика сил связи между атомами
- 27. Теория теплоемкости Эйнштейна Предположения: 1. Твердое тело – совокупность атомов, которые колеблются независимо друг от друга,
- 28. Достоинства и недостатки теории Эйнштейна Достоинства: Качественно верно описывает зависимость Cv(Т) и ее связь с жесткостью
- 29. Теория теплоемкости Дебая Основные положения: 1. При нагреве возникают связанные (коллективные) колебания атомов. Распространение колебаний в
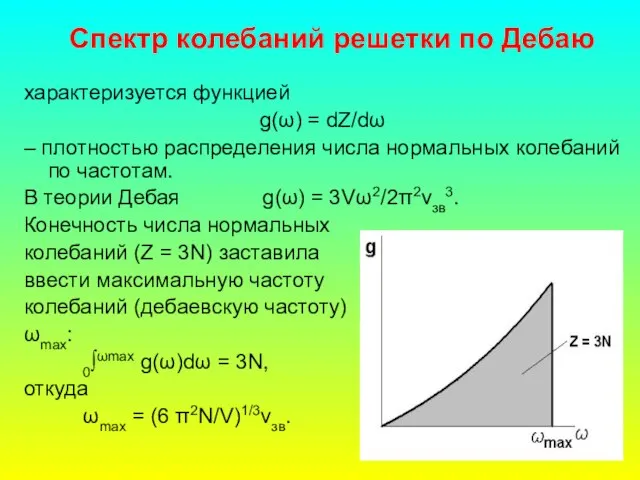
- 30. Спектр колебаний решетки по Дебаю характеризуется функцией g(ω) = dZ/dω – плотностью распределения числа нормальных колебаний
- 31. Расчет теплоемкости по Дебаю CV = ∂U/∂T = ∂/∂T 0∫ωmax g(ω) dω, CV = 9R (T/θ)3
- 32. Температура Дебая θ = ħωmax/k = (6 π2/Vат)1/3 vзв. При Т > θ возбуждены все частоты
- 33. Фононы Любую волну можно представить, как квазичастицу. Фонон – квазичастица, описывающая нормальные колебания кристаллической решетки. Энергия
- 34. Число фононов Число фононов n = 1/[exp(1/x)-1], где x = ħω/kT. Общее число фононов Nфон =
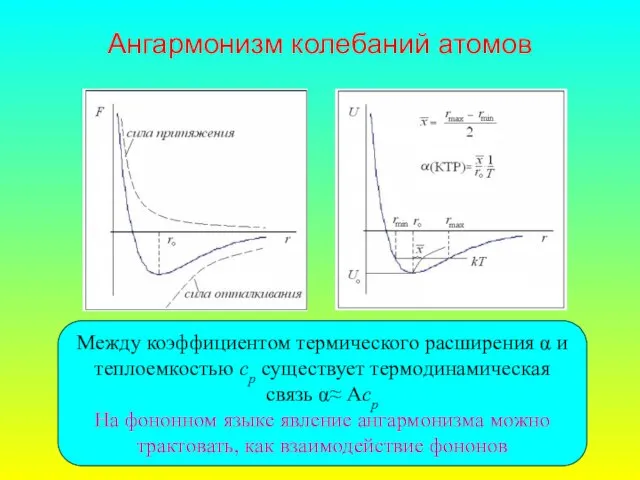
- 35. Ангармонизм колебаний атомов Между коэффициентом термического расширения α и теплоемкостью ср существует термодинамическая связь α≈ Аср
- 36. Влияние ангармонизма колебаний атомов на теплоемкость Решеточная теплоемкость с учетом ангармонизма равна: Здесь : g –
- 37. Вакансионный вклад в теплоемкость Равновесная концентрация вакансий: Появление вакансий приводит к росту энтальпии Вакансионный вклад в
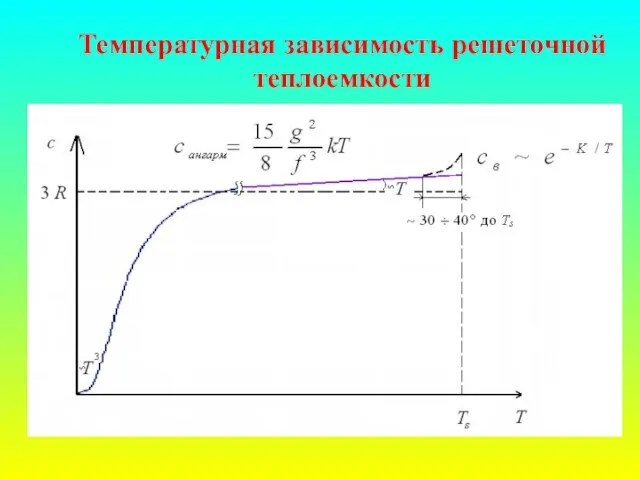
- 38. Температурная зависимость решеточной теплоемкости
- 39. Заключение Теплоемкость «скачет» - существует вклад, зависящий от положения в таблице Менделеева При высоких температурах реальная
- 40. Лекция 3. 1 час. Электронная составляющая теплоемкости 3.1 Электронная составляющая теплоемкости простых и переходных металлов. Общие
- 41. энергия Ферми Рассмотрим энергетический спектр одновалентного металла – в его зоне N-уровней, но занято N/2 Значение
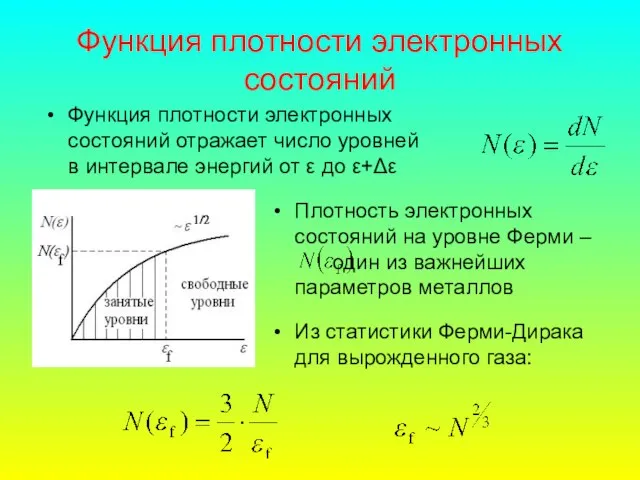
- 42. Функция плотности электронных состояний Функция плотности электронных состояний отражает число уровней в интервале энергий от ε
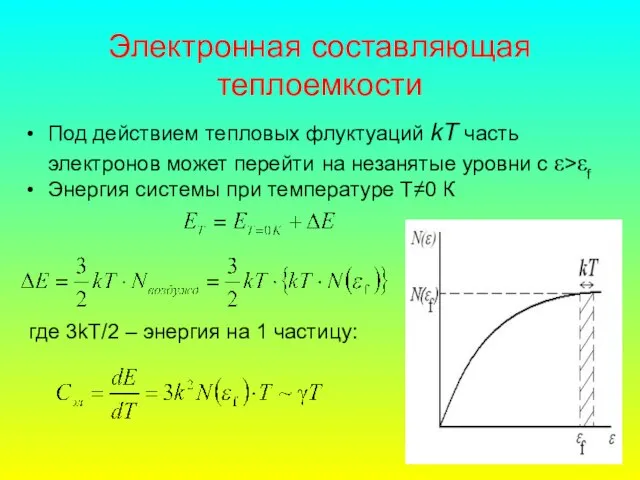
- 43. Электронная составляющая теплоемкости Под действием тепловых флуктуаций kT часть электронов может перейти на незанятые уровни с
- 44. Анализ электронной составляющей теплоемкости простых металлов Учет неидеальности, не одновалентности и квантовой статистики Оценка Сэл при
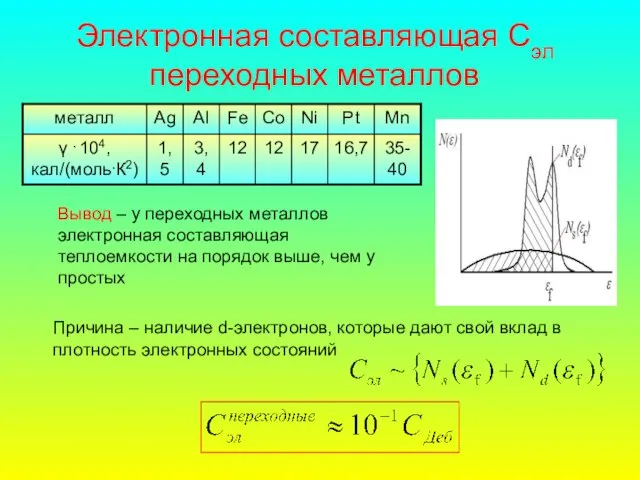
- 45. Электронная составляющая Сэл переходных металлов Вывод – у переходных металлов электронная составляющая теплоемкости на порядок выше,
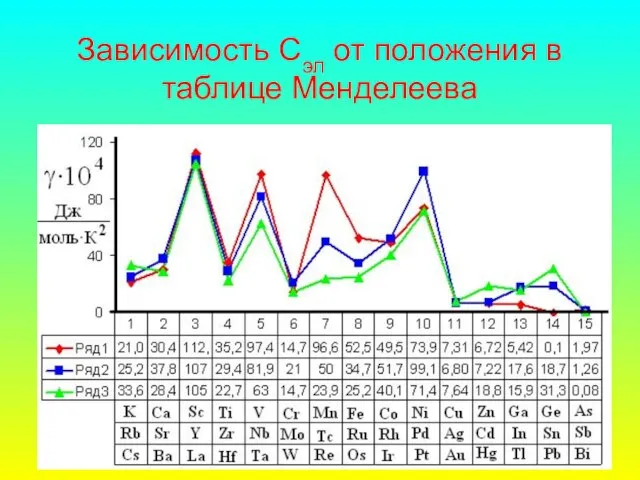
- 46. Зависимость Сэл от положения в таблице Менделеева
- 47. Магноны и их влияние на теплоемкость Магнон – квазичастица, описывающая магнитное возмущение спиновой системы ↑↑↑↑↑↑↑↑ -
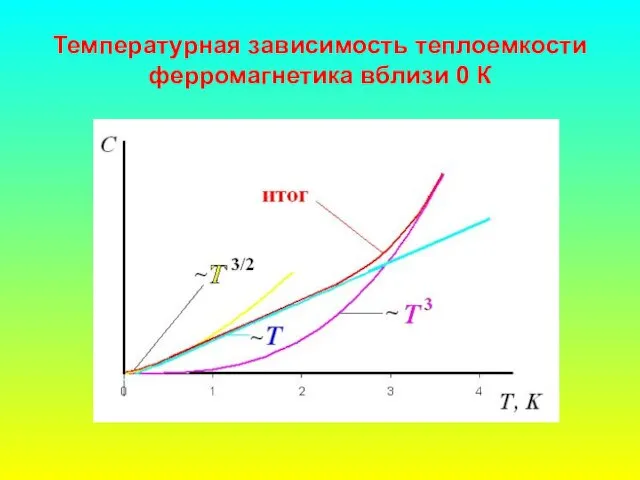
- 48. Температурная зависимость теплоемкости ферромагнетика вблизи 0 К
- 49. Лекция 3. Час 2 Поведение теплоемкости при фазовых переходах.
- 50. Связь теплоемкости с функциями термодинамического состояния и энергией Гиббса Фазовые переходы бывают 1 и 2 рода
- 51. Особенности ФП 1 и 2 рода
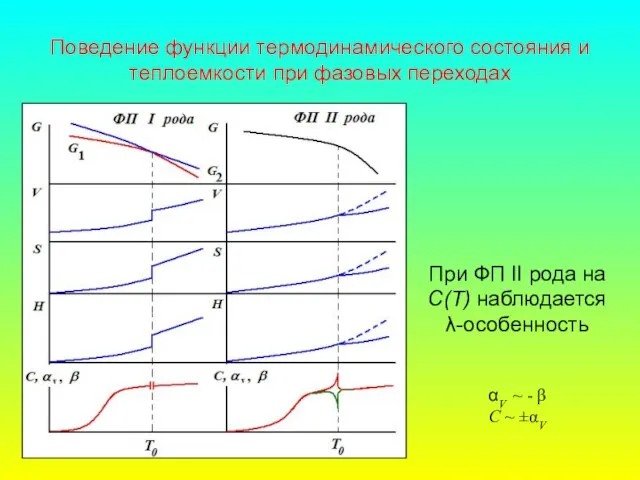
- 52. Поведение функции термодинамического состояния и теплоемкости при фазовых переходах При ФП II рода на С(Т) наблюдается
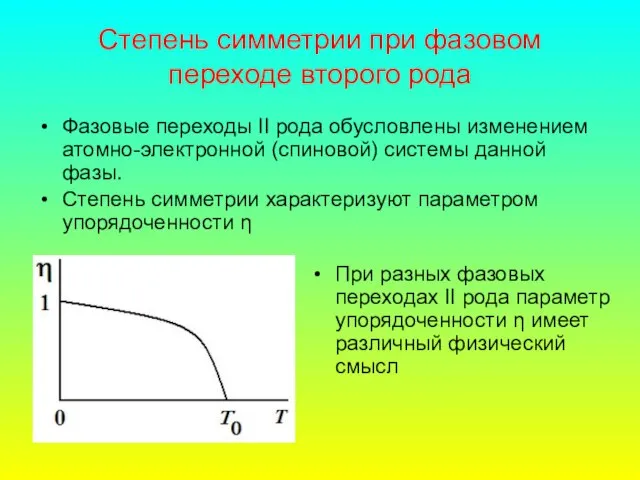
- 53. Степень симметрии при фазовом переходе второго рода Фазовые переходы II рода обусловлены изменением атомно-электронной (спиновой) системы
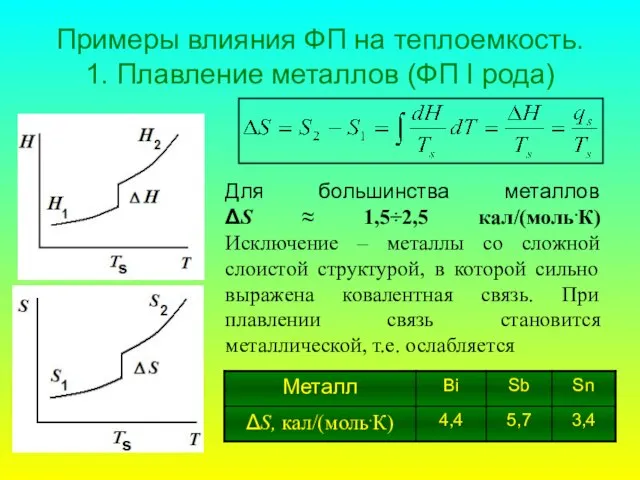
- 54. Примеры влияния ФП на теплоемкость. 1. Плавление металлов (ФП I рода) Для большинства металлов ΔS ≈
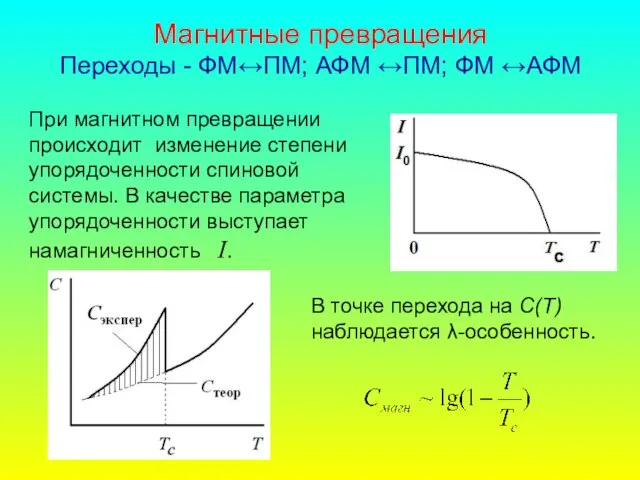
- 55. Магнитные превращения Переходы - ФМ↔ПМ; АФМ ↔ПМ; ФМ ↔АФМ При магнитном превращении происходит изменение степени упорядоченности
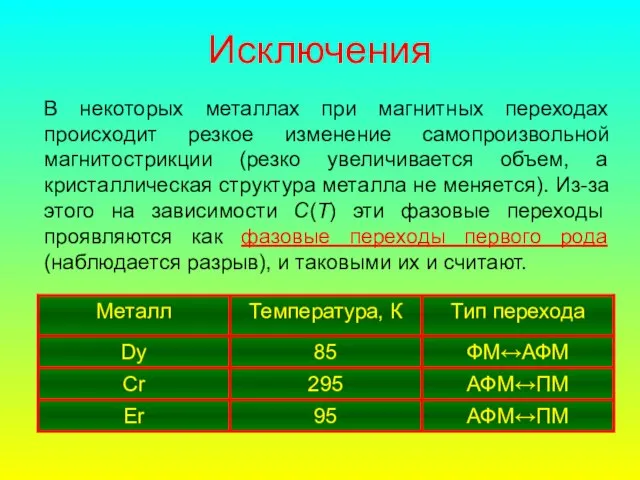
- 56. Исключения В некоторых металлах при магнитных переходах происходит резкое изменение самопроизвольной магнитострикции (резко увеличивается объем, а
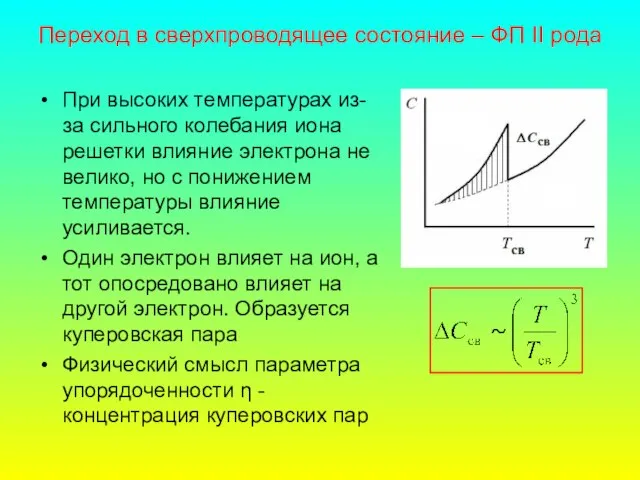
- 57. Переход в сверхпроводящее состояние – ФП II рода При высоких температурах из-за сильного колебания иона решетки
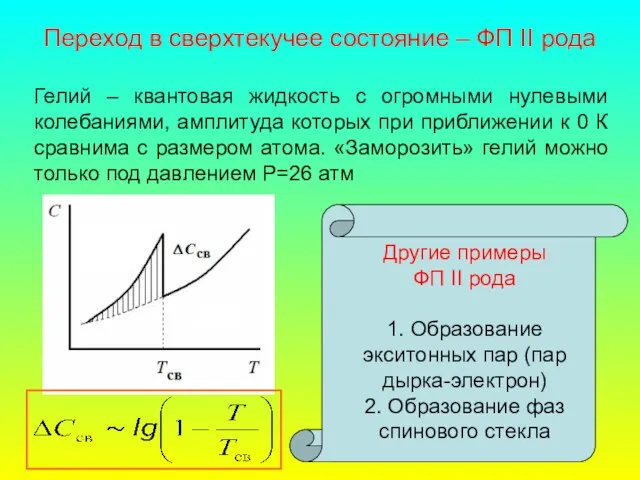
- 58. Переход в сверхтекучее состояние – ФП II рода Гелий – квантовая жидкость с огромными нулевыми колебаниями,
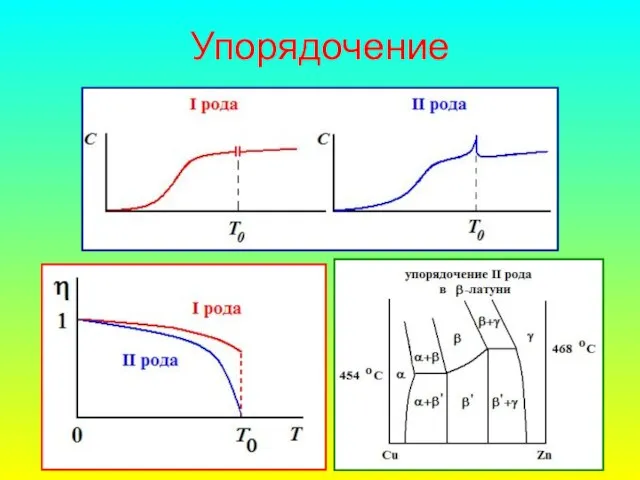
- 59. Упорядочение
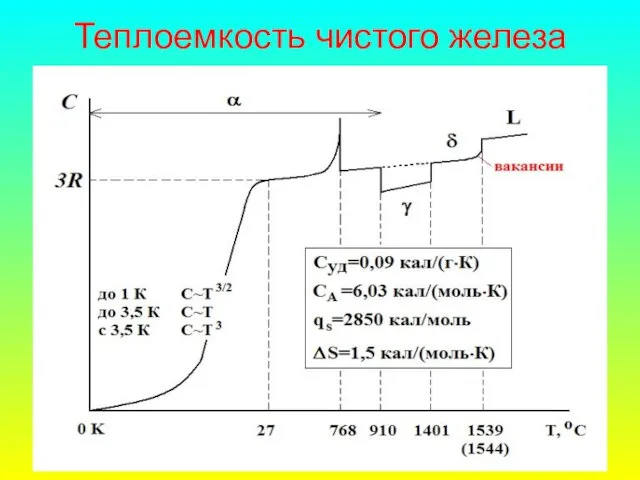
- 60. Теплоемкость чистого железа
- 61. Лекция 4. час 1 Теплоемкость сплавов и соединений
- 62. Теплоемкость сплавов Все изложенные ранее закономерности выполняются и для сплавов. Имеющиеся отличия обусловлены тем, что при
- 63. Расчет теплоемкости соединения Для теплоемкости при Т > θ справедливо правило аддитивности Неймана-Коппа : где x1
- 64. Расчет теплоемкости гетерогенной системы где q1 и q2 – массовые доли. Пример: Латунь Л80 (80%Cu+20%Zn) Cуд(Cu)=0,0909
- 65. Примеры расчета для У8
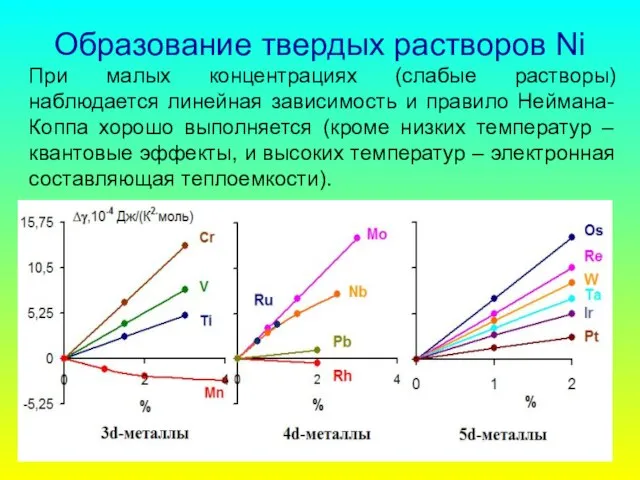
- 66. Образование твердых растворов Ni При малых концентрациях (слабые растворы) наблюдается линейная зависимость и правило Неймана-Коппа хорошо
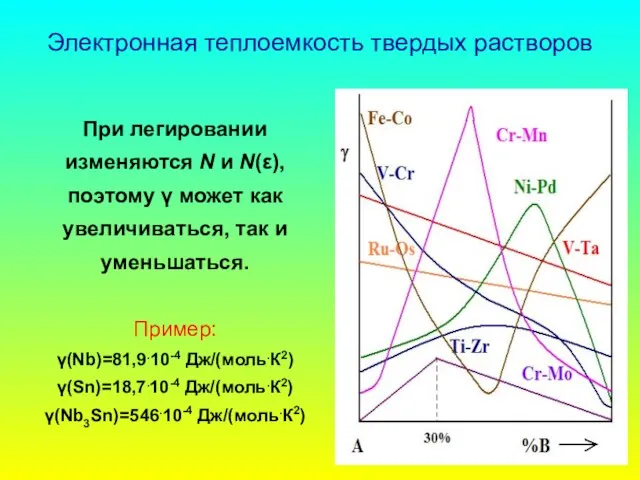
- 67. Электронная теплоемкость твердых растворов При легировании изменяются N и N(ε), поэтому γ может как увеличиваться, так
- 68. Лекция 4. час 2. 2.4. Зависимость теплоемкости от размеров структурных составляющих материалов. Теплоемкость сплавов в кристаллическом,
- 69. Теплоемкость наноматериалов Теплоемкость наноматериалов отличается от теплоемкости массивного материала такого же химического и фазового состава. Причины:
- 70. Влияние размера дисперсных частиц на cпектр колебаний решетки В ультрадисперсных системах могут возникать волны, длина которых
- 71. Зависимость теплоемкости от параметров частиц Теплоемкость крупнокристаллического тела объемом V по Дебаю при T Теплоемкость дисперсных
- 72. Квантовый подход к определению влияния размера частицы В квантовом приближении для сферической частицы радиусом r общее
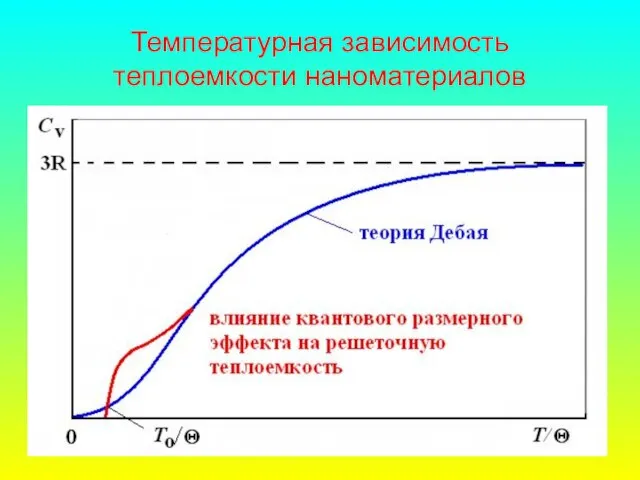
- 73. Температурная зависимость теплоемкости наноматериалов
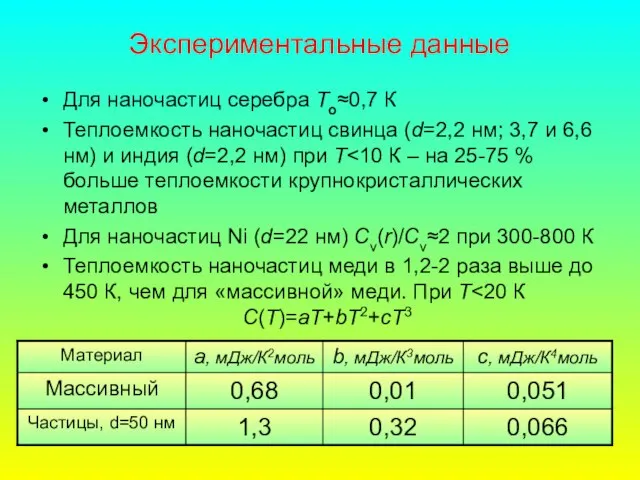
- 74. Экспериментальные данные Для наночастиц серебра То≈0,7 К Теплоемкость наночастиц свинца (d=2,2 нм; 3,7 и 6,6 нм)
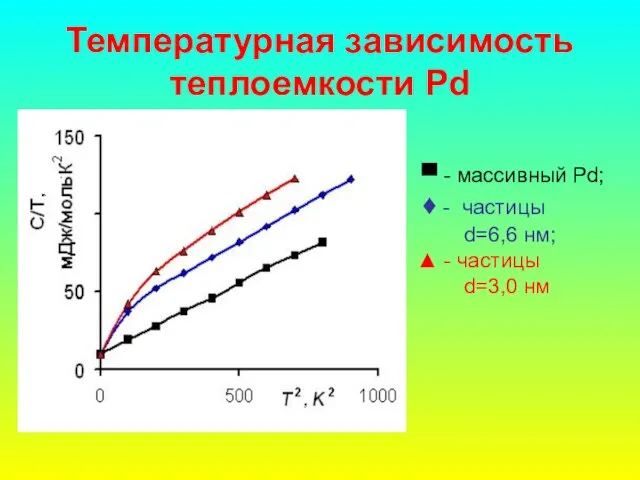
- 75. Температурная зависимость теплоемкости Pd ▀ - массивный Pd; ♦ - частицы d=6,6 нм; ▲ - частицы
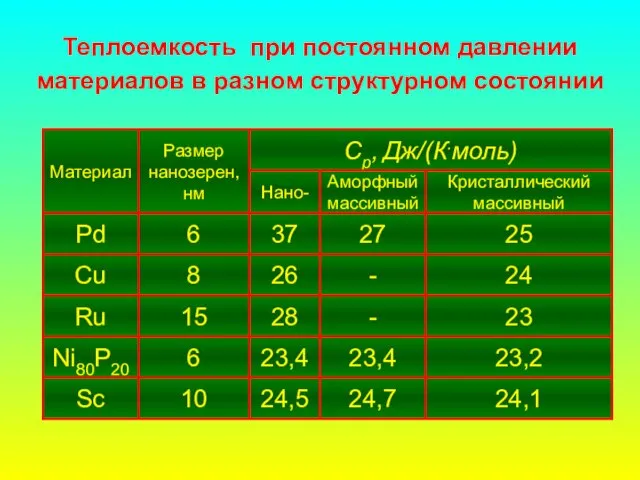
- 76. Теплоемкость при постоянном давлении материалов в разном структурном состоянии
- 77. Влияние дисперсности материала на температуру Дебая Соотношение между температурами Дебая массивного Θ и ультрадисперсного материалов Tд
- 79. Скачать презентацию











![Виды теплоемкости Теплоемкость тела: C = δQ/dT [Дж/К]. Удельная теплоемкость: Суд =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/366147/slide-16.jpg)













![Число фононов Число фононов n = 1/[exp(1/x)-1], где x = ħω/kT. Общее](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/366147/slide-33.jpg)




















 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства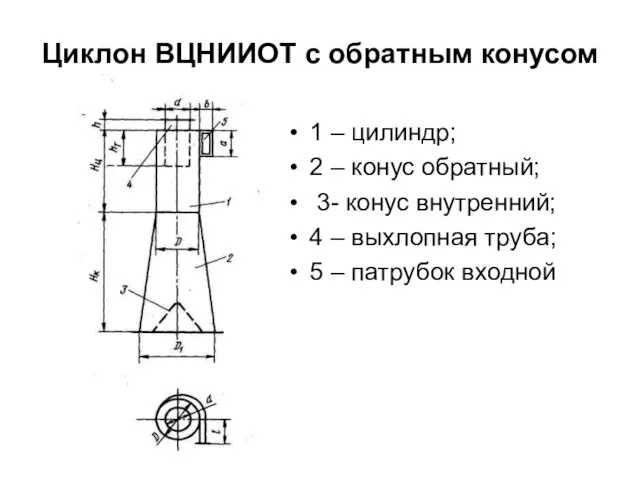 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)