Содержание
- 2. Структура темы 1. Погашение кредита единовременным платежем 2. Погашение кредита частями 3. Доходность кредитов с учетом
- 3. 1. Погашение кредита единовременным платежем При погашении кредита единовременным платежем в конце срока сумма выплат по
- 4. 2. Погашение кредита частями А) Погашение основной суммы кредита равными частями Размер уплаты в конце первого
- 5. 3. Доходность кредитов с учетом удержания комиссионных При выдаче кредита по простой ставке и удержании комиссии,
- 7. Скачать презентацию
Слайд 2Структура темы
1. Погашение кредита единовременным платежем
2. Погашение кредита частями
3. Доходность кредитов с
Структура темы
1. Погашение кредита единовременным платежем
2. Погашение кредита частями
3. Доходность кредитов с

учетом удержания комиссионных
4. Расчеты в условиях инфляции
4. Расчеты в условиях инфляции
Слайд 31. Погашение кредита единовременным платежем
При погашении кредита единовременным платежем в конце
1. Погашение кредита единовременным платежем
При погашении кредита единовременным платежем в конце

срока сумма выплат по кредиту может быть определена с использованием уже известных из предыдущей темы формул:
Для простых процентов: S= P+I=P*(1+n*i)
Для сложных процентов: S = P*(1+i)N
Аналогично, с использованием ранее приведенных формул, можно определять срок кредита, ставку процента за кредит, а также выдаваемую сумму.(см.Главу 1)
Для простых процентов: S= P+I=P*(1+n*i)
Для сложных процентов: S = P*(1+i)N
Аналогично, с использованием ранее приведенных формул, можно определять срок кредита, ставку процента за кредит, а также выдаваемую сумму.(см.Главу 1)
Слайд 42. Погашение кредита частями
А) Погашение основной суммы кредита равными частями
Размер уплаты
2. Погашение кредита частями
А) Погашение основной суммы кредита равными частями
Размер уплаты

в конце первого года, включающий основной долг и уплату процентов равен: S1=D/n+Dg, где g-годовая ставка процента по кредиту, D-сумма кредита
Сумма выплачиваемых процентов равна: I=Dg(n+1)/2
Общая сумма погашения кредита равна: S=D+I=D(1+g(n+1)/2)
Если взносы будут осуществлятся p раз в году, сумма процентов равна: I=(gD/p)*(np+1)/2 (*)
B) Погашение кредита равными срочными уплатами
Если проценты за кредит начисляются по простой ставке, то их сумма находится по формуле (*).
Расходы на погашение кредита будут равны: S=D+I
Размер одинаковых срочных выплат равен: R=(D+I)/np, n-cрок кредита в годах, p-количество уплат в год.
При погашении кредита с начислением сложных процентов:
платежи размеров R, дисконтированные на начало первого года:
A1=R/(1+i), A2=R(1+i)2, … ,An=R(1+i)n
Cумма их равна: A=R*(1-(1+i) –n )/i, отсюда находим размер платежа:
R=Di/(1-(1+i) –n )
Общая сумма погашения кредита составит: S=nR=nDi/(1-(1+i) –n)
Если платежи будут вносится p раз в году, то их размер равен:
R=D((1+i)1/p -1)/(1-(1+i) –n )
Сумма выплачиваемых процентов равна: I=Dg(n+1)/2
Общая сумма погашения кредита равна: S=D+I=D(1+g(n+1)/2)
Если взносы будут осуществлятся p раз в году, сумма процентов равна: I=(gD/p)*(np+1)/2 (*)
B) Погашение кредита равными срочными уплатами
Если проценты за кредит начисляются по простой ставке, то их сумма находится по формуле (*).
Расходы на погашение кредита будут равны: S=D+I
Размер одинаковых срочных выплат равен: R=(D+I)/np, n-cрок кредита в годах, p-количество уплат в год.
При погашении кредита с начислением сложных процентов:
платежи размеров R, дисконтированные на начало первого года:
A1=R/(1+i), A2=R(1+i)2, … ,An=R(1+i)n
Cумма их равна: A=R*(1-(1+i) –n )/i, отсюда находим размер платежа:
R=Di/(1-(1+i) –n )
Общая сумма погашения кредита составит: S=nR=nDi/(1-(1+i) –n)
Если платежи будут вносится p раз в году, то их размер равен:
R=D((1+i)1/p -1)/(1-(1+i) –n )
Слайд 53. Доходность кредитов с учетом удержания комиссионных
При выдаче кредита по простой
3. Доходность кредитов с учетом удержания комиссионных
При выдаче кредита по простой

ставке и удержании комиссии, S=(P-дельтаP)(1+n*iэ), где P-сумма кредита, дельтаP-комиссионные, n-срок кредита в годах.
По другому комиссионные можно записать как дельтаP=G*P, где G-доля комиссионных.
Из P(1+ni)=P(1-G)(1+n*iэ), получаем эффективную ставку простых процентов по кредиту с учетом удержания комиссии: iэ=(ni+G)/n(1-G), где n может быть равным q/K, где K-дни в году, q-срок кредита в днях.
При выдаче долгосрочного кредита по сложной ставке процентов g на n лет, с учетом удержания комиссионных:
P(1+g)n=P(1-G)(1+iэ)n , отсюда эффективная ставка по кредиту с учетом удержания комиссионных равна:
iэ=1+g/(корень степени n от (1-G)) - 1
По другому комиссионные можно записать как дельтаP=G*P, где G-доля комиссионных.
Из P(1+ni)=P(1-G)(1+n*iэ), получаем эффективную ставку простых процентов по кредиту с учетом удержания комиссии: iэ=(ni+G)/n(1-G), где n может быть равным q/K, где K-дни в году, q-срок кредита в днях.
При выдаче долгосрочного кредита по сложной ставке процентов g на n лет, с учетом удержания комиссионных:
P(1+g)n=P(1-G)(1+iэ)n , отсюда эффективная ставка по кредиту с учетом удержания комиссионных равна:
iэ=1+g/(корень степени n от (1-G)) - 1
 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве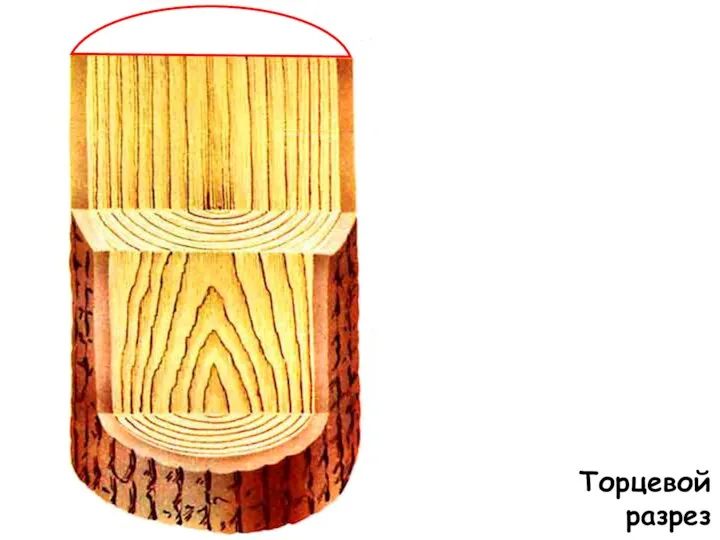 Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства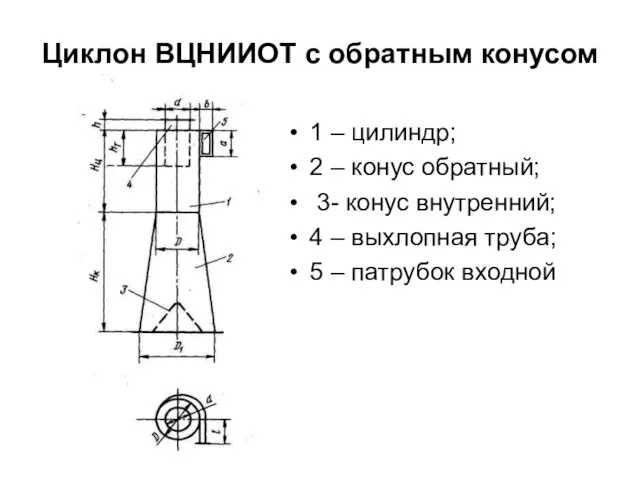 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)