Основи логічного програмування

Основи логічного програмування
1. (∀x)(∃y)(∀z)(∀u)(∃v)(∃w)M(x,y,z,u,v,w)
Скулемівська нормальна форма:
(∀x)(∀z)(∀u)M(x,f(x),z,u,g(x,z,u),h(x,z,u))
Безкванторна форма:
M(x,f(x),z,u,g(x,z,u),h(x,z,u))
2. (∃x)(∀y)(∃z)(∀u)(∃v)N(x,y,z,u,v) Безкванторна форма: N(a,y,f(y),u,g(y,u))
3.(∃x)(∀y)P(y,x,y)
Безкванторна форма: P(y,e,y)
(при інтерпретації I
PI(y,z,u)=true ⇔ y•z=u
маємо умову існування правої одиниці: “e – права одиниця”)
Скулемівська нормальна форма.
Безкванторна форма

Основи логічного програмування
1. Кон’юнктивна нормальна форма (матриці або безкванторної частини):
(¬P(x)v Q(x,f(x))) & P(g(a)) & ¬Q(y,z)
Множина диз’юнктів:
{ ¬P(x)v Q(x,f(x)),
P(g(a)),
¬Q(y,z)}
2. P(x,y,u) & P(y,z,v)& P(x,v,w) ⊃ P(u,z,w)
(при інтерпретації I: PI(y,z,u)=true ⇔ y•z=u
маємо умову асоціативності).
Множина диз'юнктів:
{¬ P(x,y,u) v ¬ P(y,z,v) v ¬P(x,v,w) v P(u,z,w)}
Кон’юнктивна нормальна форма. Множина диз’юнктів (1/2)

Основи логічного програмування
3. P(x,y) & P(y,z) ⊃ Q(x,z)
(при інтерпретації I:
PI(x,y)=true ⇔ “x є батьком y”;
QI(x,y)=true ⇔ “x є дідом y”
маємо умову, що пов'язує відношення батьківства і дідівства).
Множина диз'юнктів:
{¬ P(x,y) v ¬ P(y,z) v Q(x,z)}
Кон’юнктивна нормальна форма. Множина диз’юнктів (2/2)

Основи логічного програмування
Правило резолюції:
Δ1 v C, Δ2 v ¬C
Δ1 v Δ2
Δ1 v Δ2 — резольвента диз'юнктів Δ1 v C, Δ2 v ¬C.
Резолютивний вивід.
Приклад.
Множина диз'юнктів:
{ P v Q, P v ¬Q, ¬P v Q, ¬P v ¬Q }
1) P v Q;
2) P v ¬Q;
3) ¬P v Q;
4) ¬P v ¬Q;
--------------
5) P (резольвента диз'юнктів 1 та 2) ;
6) ¬P (резольвента диз'юнктів 3 та 4);
7) — порожній диз'юнкт (резольвента диз'юнктів 5 та 6).
Метод резолюцій для логіки висловлювань (1/4)

Основи логічного програмування
Теорема про повноту. Множина диз'юнктів M є суперечливою тоді і тільки тоді, коли для множини M існує резолютивний вивід порожнього диз'юнкту.
Типова задача: Чи є Q логічним наслідком P1, P2, … , Pk ?
P1& P2 & … & Pk ⊃ Q - true ?
¬(P1& P2 & … & Pk ⊃ Q) - false ? (Суперечливість!)
Перетворимо ¬(P1& P2 & … & Pk ⊃ Q):
¬(¬(P1& P2 & … & Pk ) v Q);
P1& P2 & … & Pk & (¬Q).
Отже, диз'юнкти можуть визначатись безпосередньо з формул P1, P2, … , Pk та ¬Q.
Метод резолюцій для логіки висловлювань (2/4)

Основи логічного програмування
Теорема про повноту. Множина диз'юнктів M є суперечливою тоді і тільки тоді, коли для множини M існує резолютивний вивід порожнього диз'юнкту.
Типова задача: Чи є Q логічним наслідком P1, P2, … , Pk ?
Диз'юнкти можуть визначатись безпосередньо з формул P1, P2, … , Pk та ¬Q.
Метод резолюцій для логіки висловлювань (3/4)

Основи логічного програмування
Приклад. Чи є P ⊃ R логічним наслідком P ⊃ Q та Q ⊃ R? (Транзитивність імплікації)
1) ¬P v Q (диз'юнкт для P ⊃ Q );
2) ¬Q v R (диз'юнкт для Q ⊃ R);
3-4) P, ¬R (два диз'юнкти для ¬(P ⊃ R) );
--------------
5) Q (резольвента диз'юнктів 1 та 3) ;
6) ¬Q (резольвента диз'юнктів 2 та 4);
7) — порожній диз'юнкт (резольвента диз'юнктів 5 та 6).
Метод резолюцій для логіки висловлювань (4/4)

Основи логічного програмування
1) P v Q;
2) P v ¬Q;
3) ¬P v Q;
4) ¬P v ¬Q;
--------------
5) P (резольвента диз'юнктів 1 та 2) ;
6) ¬P (резольвента диз'юнктів 3 та 4);
7) — порожній диз'юнкт (резольвента диз'юнктів 5 та 6).
Протиріччя у випадку логіки предикатів може бути не таке наочне:
P(x), ¬P(f(a)).
Застосування підстановок, у даному випадку замість x можна підставити f(a).
Процедура (алгоритм) уніфікації. Підстановки замість змінних.
Протиріччя у випадках логіки висловлювань і логіки предикатів
Дві формули, що відрізняються лише знаком

Основи логічного програмування
P(x,f(x),a), P(g(z),y,u)
1. x←g(z);
P(g(z),f(g(z)),a), P(g(z),y,u).
2. y←f(g(z));
P(g(z),f(g(z)),a), P(g(z),f(g(z)),u).
3. u←a;
P(g(z),f(g(z)),a), P(g(z),f(g(z)),a).
σ = {x←g(z)}•{y←f(g(z))}•{u←a} — найбільш загальний уніфікатор (НЗУ)
------------------------------------------------------
σ1 = {x←g(a)}•{y←f(g(a))}•{u←a} — інший уніфікатор (але не НЗУ)
σ1 = σ•{z←a}
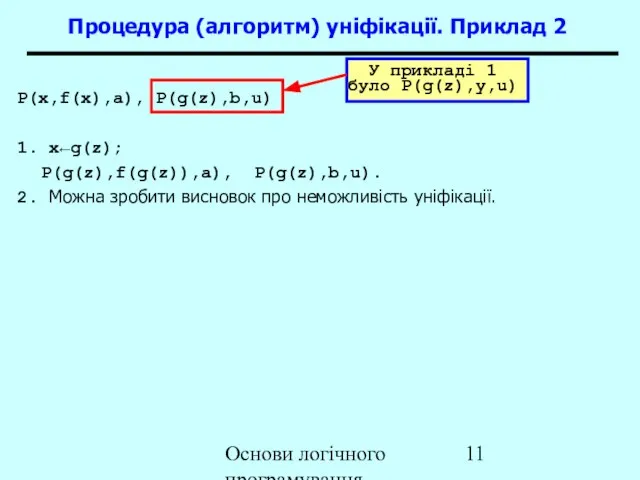
Процедура (алгоритм) уніфікації. Приклад 1

Основи логічного програмування
P(x,f(x),a), P(g(z),b,u)
1. x←g(z);
P(g(z),f(g(z)),a), P(g(z),b,u).
2. Можна зробити висновок про неможливість уніфікації.
Процедура (алгоритм) уніфікації. Приклад 2
У прикладі 1 було P(g(z),y,u)

Основи логічного програмування
Правило (бінарної) резолюції:
F1 = Δ1 v C1, F2 = Δ2 v ¬C2 (C1, C2 — уніфіковані з НЗУ σ)
σ(Δ1 v Δ2)
σ(Δ1 v Δ2) — (бінарна) резольвента диз'юнктів F1 = Δ1 v C1, та F2 = Δ2 v ¬C2.
Резолютивний вивід.
Приклад.
Множина диз'юнктів:
{P(x), ¬P(f(a))}
1) P(x);
2) ¬P(f(a));
--------------
3) — бінарна резольвента диз'юнктів 1 та 2 з НЗУ σ= (x←f(a)).
Правило бінарної резолюції

Основи логічного програмування
Приклад 1.
1. P(x,y) & P(y,z) ⊃ Q(x,z)
(при інтерпретації I:
PI(x,y)=true ⇔ “x є батьком y”;
QI(x,y)=true ⇔ “x є дідом y”
маємо умову, що пов'язує відношення батьківства і дідівства).
Множина диз'юнктів:
{¬ P(x,y) v ¬ P(y,z) v Q (x,z)}
2. (∀v)(∃y) P(y,v) — ”у кожного є батько” .
Множина диз'юнктів:
{P(f(v),v)} ( f(v) — батько v) __________________________________________________________
Cпробуємо довести, що “кожен має діда” —(∀y)(∃u) Q (u,y).
Для ¬ (∀y)(∃u) Q (u,y) множина диз'юнктів:
{¬Q(u,a)}
Правило бінарної резолюції. Приклад 1 (1/3)

Основи логічного програмування
1) ¬ P(x,y) v ¬ P(y,z) v Q(x,z);
2) P(f(v),v) ;
3) ¬Q(u,a);
------------------
4) ¬ P(y,z) v Q(f(y),z) (бінарна резольвента
диз'юнктів 1 та 2 при σ= (x←f(v))•(v←y);
5) Q(f(f(z)),z) (бінарна резольвента диз'юнктів 4 та
2 при σ1= (y←f(v))•(v←z);
6) — бінарна резольвента диз'юнктів 3 та 5 при можна отримати відповідь на питання, хто ж є дідом a
σ2= (u←f(f(z))•(z←a).
Приклад 1. Продовження
Q(u,a)=true ⇔ “u є дідом a”
Аналізуючи σ2, можна по суті отримати відповідь на поставлене питання, хто ж є дідом a:
u←f(f(a))

Основи логічного програмування
Q(u,a) ⊃ ANS(u); “Хто ж є дідом a?”
¬Q(u,a) v ANS(u);
1) ¬ P(x,y) v ¬ P(y,z) v Q(x,z);
2) P(f(v),v) ;
3) ¬Q(u,a) v ANS(u); ------------------
4) ¬ P(y,z) v Q(f(y),z) (бінарна резольвента
диз'юнктів 1 та 2 при σ= (x←f(v))•(v←y);
5) Q(f(f(z)),z) (бінарна резольвента диз'юнктів 4 та
2 при σ1= (y←f(v))•(v←z);
6) ANS(f(f(a))) — бінарна резольвента диз'юнктів 3 та 5
при σ2= (u←f(f(z))•(z←a).
Приклад 1. ANS-предикат
Відповідь на поставлене запитання – “Хто ж є дідом a?”

Основи логічного програмування
Приклад 2.
1) ¬ P(x,y,u) v ¬ P(y,z,v) v ¬P(x,v,w) v P(u,z,w);
2) P(g(x1,y1),x1,y1); “існування лівого розв'язку”
3) P(x2,h(x2,y2),y2); “існування правого розв'язку”
4) ¬ P(k(e),e,k(e)); заперечення “існування правої одиниці”
------------------
5) ¬ P(y,z,v) v ¬P(g(y,u),v,w) v P(u,z,w);
(з 1, 2 при x←g(x1,y1),x1←y, y1←u )
6) ¬ P(y,z,y) v P(u,z,u);
(з 5, 2 при x1←y, y1←u v←y, w←u);
7) P(u, h(y,y),u);
(з 6, 3 при x2←y, z←h(y,y2), y2←y);
8) — (з 7, 4 при u← k(e), e←h(y,y))
Правило бінарної резолюції. Приклад 2
¬(∃e)(∀x) P(x,e,x)
(∀e)(∃x)¬ P(x,e,x)
(∀x1)(∀y1)(∃y) P(y,x1,y1)–
“існування лівого розв'язку”

Основи логічного програмування
1) ¬ P(x,y,u) v ¬ P(y,z,v) v ¬P(x,v,w) v P(u,z,w);
2) P(g(x1,y1),x1,y1);
3) P(x2,h(x2,y2),y2);
4) ¬ P(k(e),e,k(e)) v ANS(e);
------------------------------
5) ¬ P(y,z,v) v ¬P(g(y,u),v,w) v P(u,z,w);
(з 1, 2 при x←g(x1,y1),x1←y, y1←u )
6) ¬ P(y,z,y) v P(u,z,u);
(з 5, 2 при x1←y, y1←u v←y, w←u);
7) P(u,h(y,y),u);
(з 6, 3 при x2←y, z←h(y,y2), y2←y);
8) ANS(h(y,y)); (з 7, 4 при u← k(e), e←h(y,y)).
Правою одиницею є значення e=h(y,y), тобто розв’язок X рівняння yX=y
для довільного y.
Приклад 2. Продовження