Содержание
- 2. Содержание: Определение симметрии, виды симметрии. Осевая симметрия. Теорема.
- 3. Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость в расположении частей. Виды симметрии: 1. осевая симметрия 2.
- 4. Осевой симметрией с осью a называется такое отображение пространства на себя, при котором любая точка M
- 5. Докажем , что осевая симметрия есть движение.
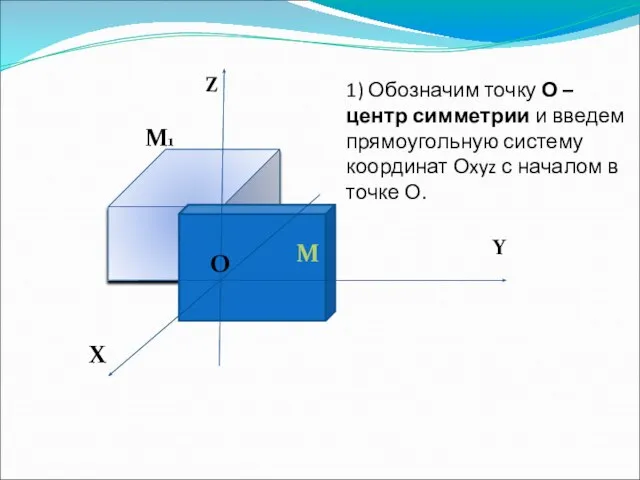
- 6. Z Y X O O M M1 1) Обозначим точку О – центр симметрии и введем
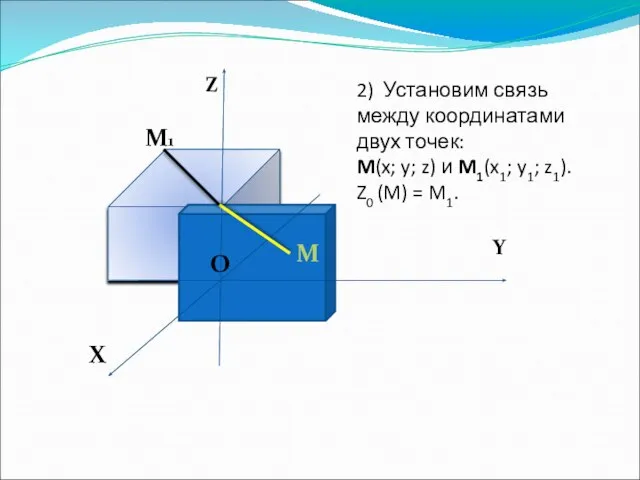
- 7. Z Y X O O M M1 2) Установим связь между координатами двух точек: M(x; y;
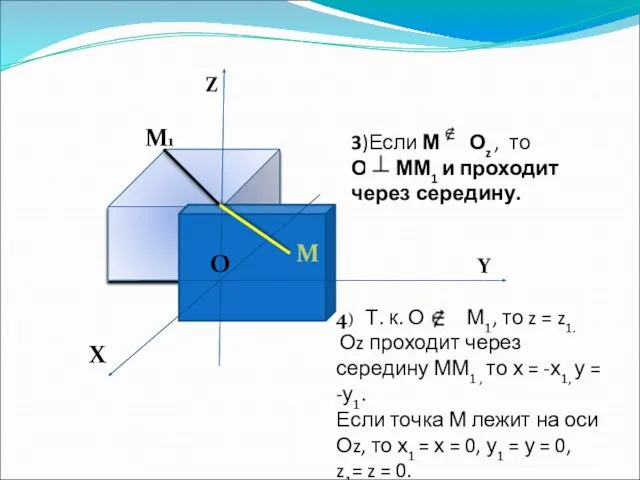
- 8. Z Y X O O M M1 3)Если М Оz , то Оz ММ1 и проходит
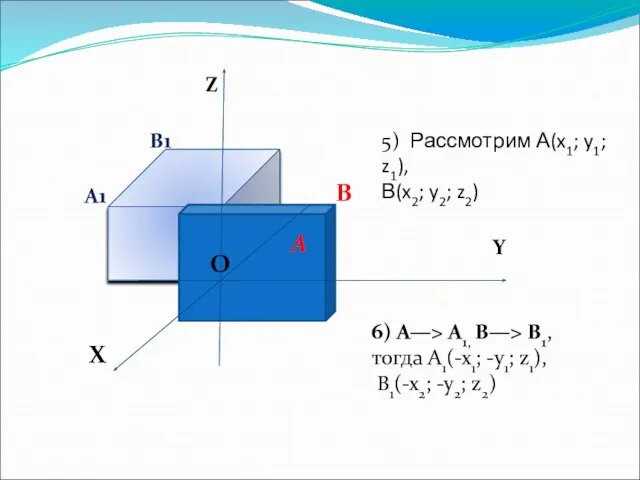
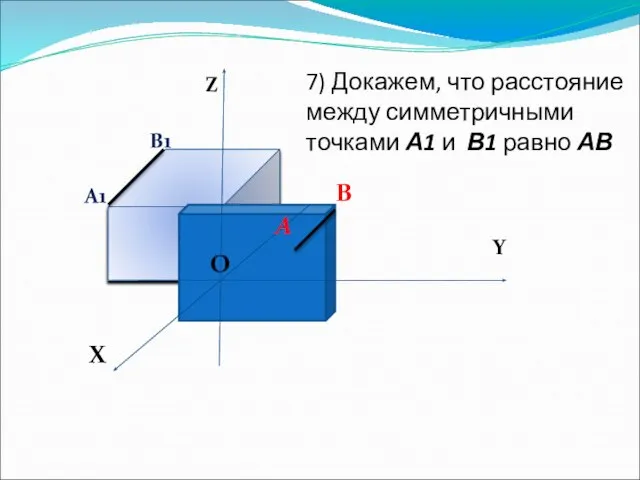
- 9. Z Y X O O A B A1 B1 5) Рассмотрим А(x1; y1; z1), В(x2; y2;
- 10. Z Y X O O A B A1 B1 тогда АВ=А1В1, т.е. Sоz - движение. 7)
- 12. Скачать презентацию




 Использование ИКТпри отработке навыков контроля и самоконтроля на уроках русского языка
Использование ИКТпри отработке навыков контроля и самоконтроля на уроках русского языка Что такое море?
Что такое море? Своя Игра. Первый тур
Своя Игра. Первый тур Великобритания
Великобритания Заключительный этап проекта
Заключительный этап проекта Основы стандартизации
Основы стандартизации Настя Степанова
Настя Степанова Психология девиантного поведения
Психология девиантного поведения Роль международного разделения труда в системе современной мировой экономики и международных экономических отношений
Роль международного разделения труда в системе современной мировой экономики и международных экономических отношений 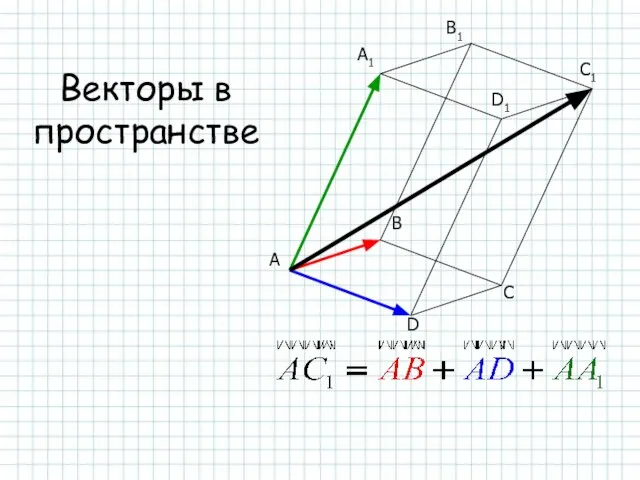 Векторы в пространстве
Векторы в пространстве Глаголдорыҥ лексика учуры, грамматика темдектери
Глаголдорыҥ лексика учуры, грамматика темдектери Подготовка к глобальной империи
Подготовка к глобальной империи Комплексный анализ текста. Подготовка к написанию сочинения-рассуждения
Комплексный анализ текста. Подготовка к написанию сочинения-рассуждения Аборт и его осложнения
Аборт и его осложнения Файл. Файловая структура.
Файл. Файловая структура. Завтрак - это энергия
Завтрак - это энергия ПЕДАГОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ И ЕЁ ОСОБЕННОСТИ
ПЕДАГОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ И ЕЁ ОСОБЕННОСТИ Взаимодействие муниципалитета и средств массовой информации
Взаимодействие муниципалитета и средств массовой информации 10
10 Презентация на тему Буква Ё
Презентация на тему Буква Ё  Тема любви в рассказах И.А.Бунина
Тема любви в рассказах И.А.Бунина Мифология древнего востока
Мифология древнего востока Болезни сальных желез
Болезни сальных желез Социальные проблемы повести Николая Васильевича Гоголя «Вий»
Социальные проблемы повести Николая Васильевича Гоголя «Вий» 5 – 9 классы Учебники русского языка Учебники – основные компоненты учебно-методических комплектов Авторы: С.И. ЛЬВОВА, В.В. ЛЬВОВ.
5 – 9 классы Учебники русского языка Учебники – основные компоненты учебно-методических комплектов Авторы: С.И. ЛЬВОВА, В.В. ЛЬВОВ. Новосибирск 2008
Новосибирск 2008 Развитие творческих способностей младших школьников
Развитие творческих способностей младших школьников Не с причастиями
Не с причастиями