Прямоугольный треугольник

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
25
7
AB = 7; BC = 25; CD = 10.
K
Найти:
1) AC;
2) AD;
26
3) Высоту СК в ΔAСD;
24

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
25
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
4) sin(DAC);
5) tgB;
6) cos(ACB);
24
AD=26

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
25
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
AD=26
7) Средние линии ΔABC;
3,5; 12; 12,5
8) S(ACB); S(ABCD)
24

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
25
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
24
AD=26
9) отрезки АК и KD, на которые высота СК делит гипотенузу AD в ΔDAC;

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
10) отрезки AN и NС, на которые биссектриса ∠АВС делит сторону АС в ΔАВС ;
AC = 24
AD=26
N
25
x
24 – x
;

А
С
В
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
11а) радиус окружности, описанной около Δ DAC;
11б) радиус окружности, вписанной в Δ AВC;
24
AD=26
25
10
D

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
25
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
12) медиану АМ в Δ ВAC;
13) Длину отрезка ОМ, где О – точка пересечения медиан Δ ВAC;
AD=26
М
О
AC = 24

А
С
В
D
Дано: ABCD – четырехугольник,
AB ⊥ AC; CD ⊥ AC; CK ⊥ AD;
10
25
7
AB = 7; BC = 25; CD = 10.
K
Найти:
24
14) подобные треугольники на чертеже;
24
AD=26
Δ ACD ~ Δ AKC
Δ DCA ~ Δ DKC
Δ ACD ~ Δ CKD

СПРАВОЧНИК

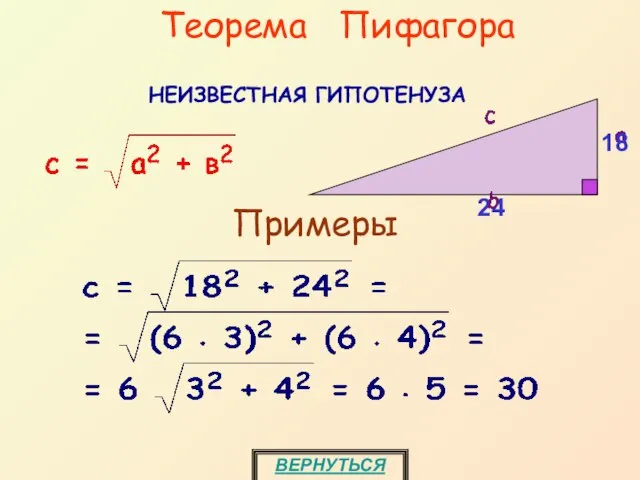
Теорема Пифагора
НЕИЗВЕСТНАЯ ГИПОТЕНУЗА
Примеры
ВЕРНУТЬСЯ
18
24

Теорема Пифагора
НЕИЗВЕСТНЫЙ КАТЕТ
Пример
ВЕРНУТЬСЯ
7
25

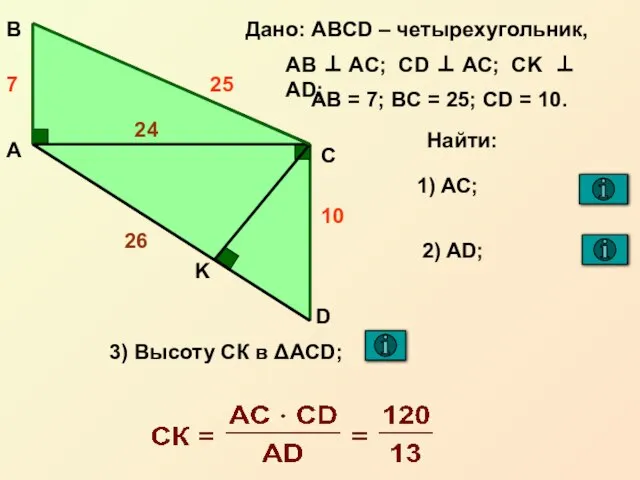
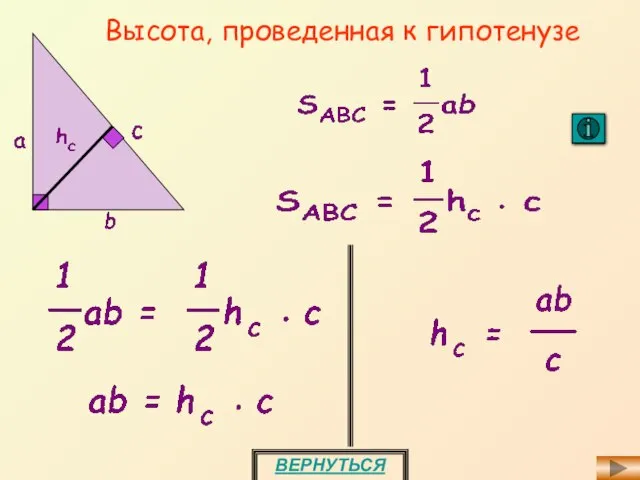
Высота, проведенная к гипотенузе
ВЕРНУТЬСЯ

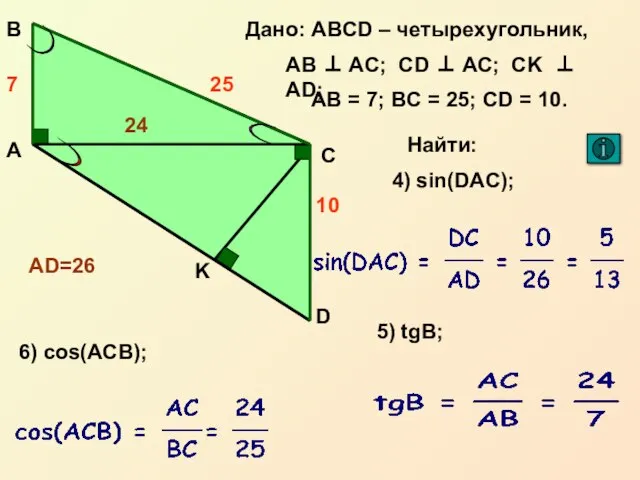
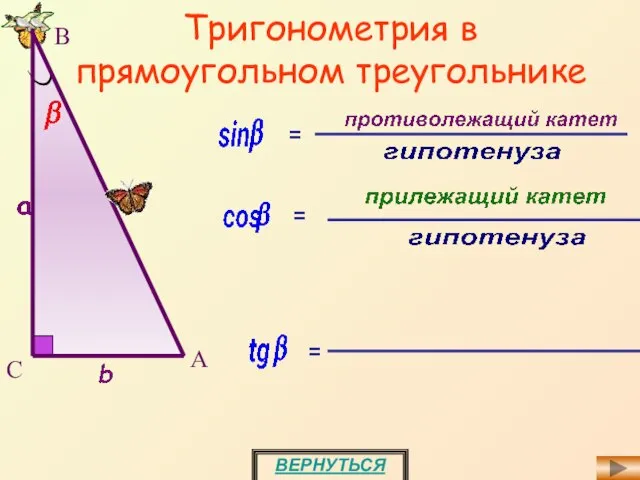
Тригонометрия в прямоугольном треугольнике
ВЕРНУТЬСЯ
=
С
А
В
=
=

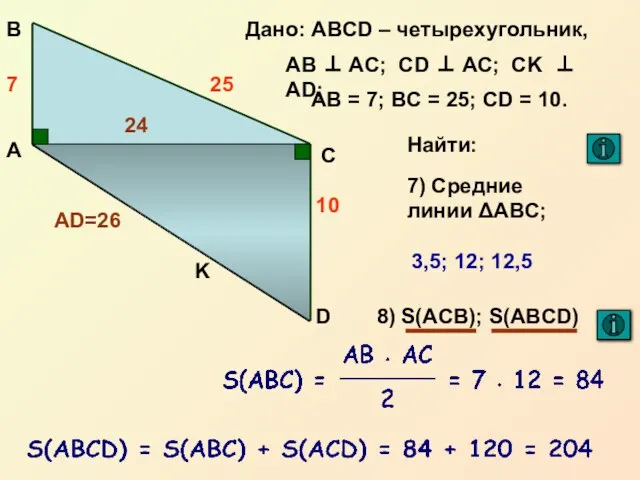
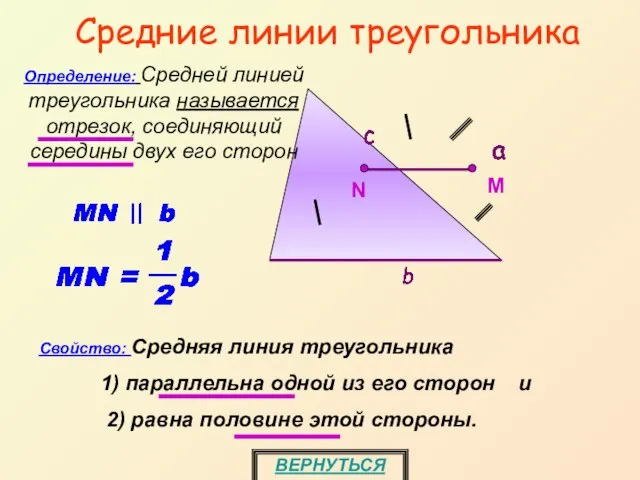
Средние линии треугольника
ВЕРНУТЬСЯ
Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон
Свойство: Средняя линия треугольника
1) параллельна одной из его сторон и
2) равна половине этой стороны.
M
N

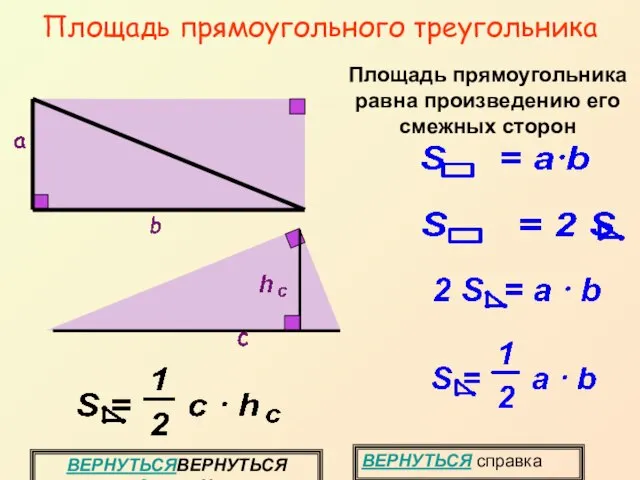
Площадь прямоугольного треугольника
ВЕРНУТЬСЯВЕРНУТЬСЯ задание № 8
Площадь прямоугольника равна произведению его смежных сторон
ВЕРНУТЬСЯ справка

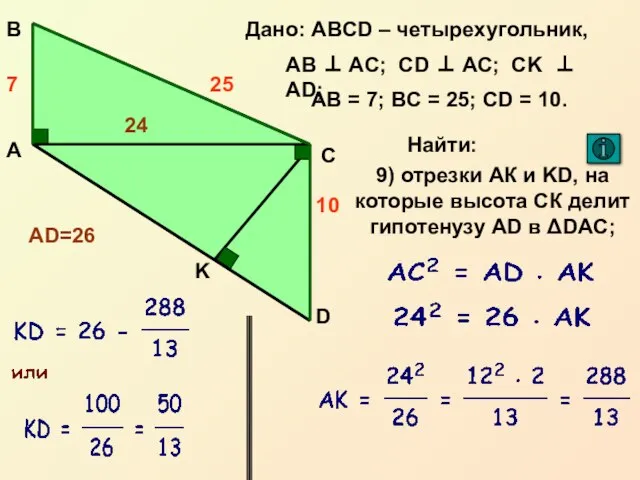
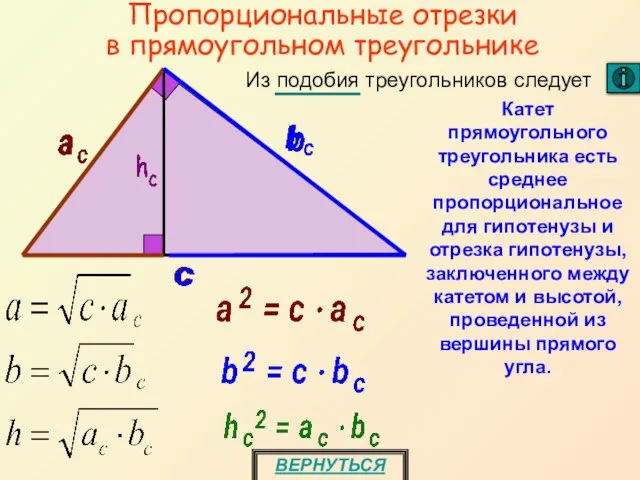
Пропорциональные отрезки
в прямоугольном треугольнике
ВЕРНУТЬСЯ
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Из подобия треугольников следует

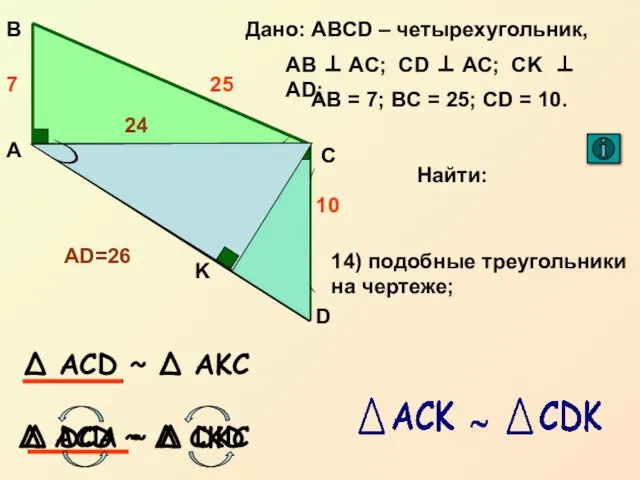
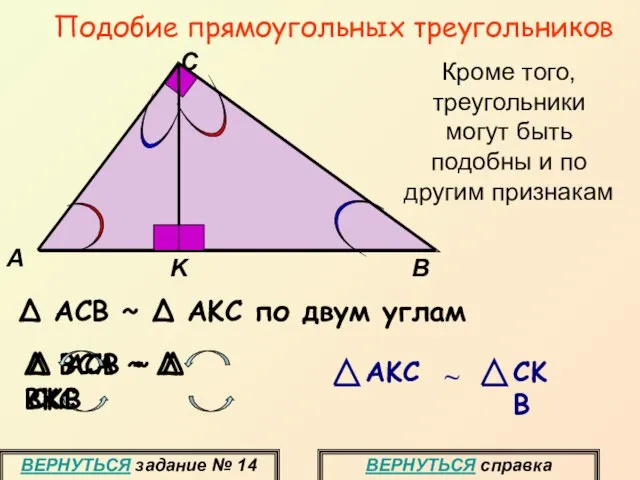
Подобие прямоугольных треугольников
Δ ACB ~ Δ AKC по двум углам
C
K
A
B
Δ BCA ~ Δ BKC
Δ ACB ~ Δ CKB
Кроме того, треугольники могут быть подобны и по другим признакам
ВЕРНУТЬСЯ задание № 14
ВЕРНУТЬСЯ справка

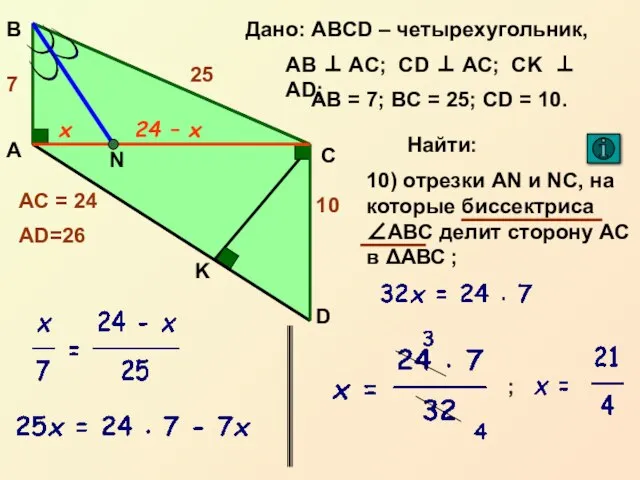
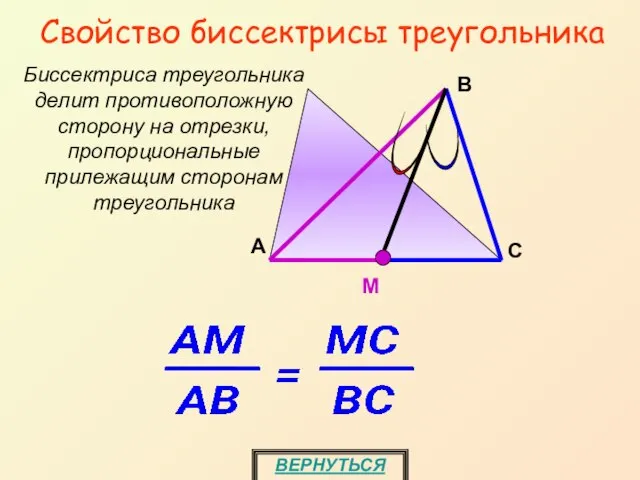
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника
M
А
С
В
ВЕРНУТЬСЯ

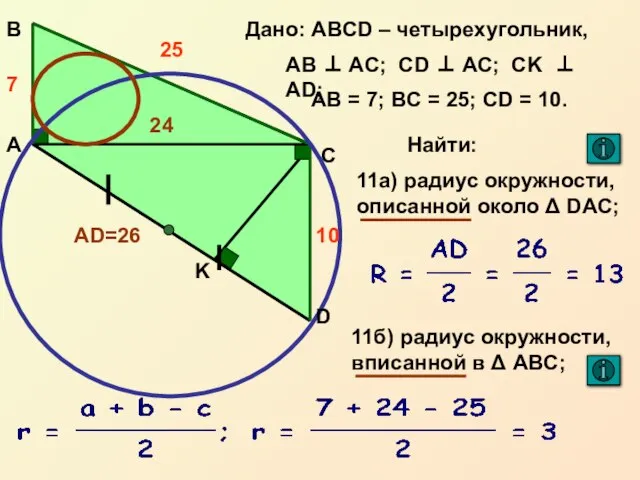
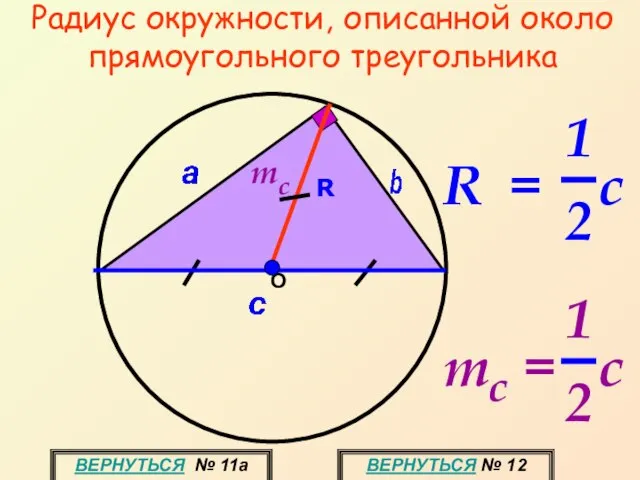
О
Радиус окружности, описанной около прямоугольного треугольника
ВЕРНУТЬСЯ № 11а
ВЕРНУТЬСЯ № 12
R

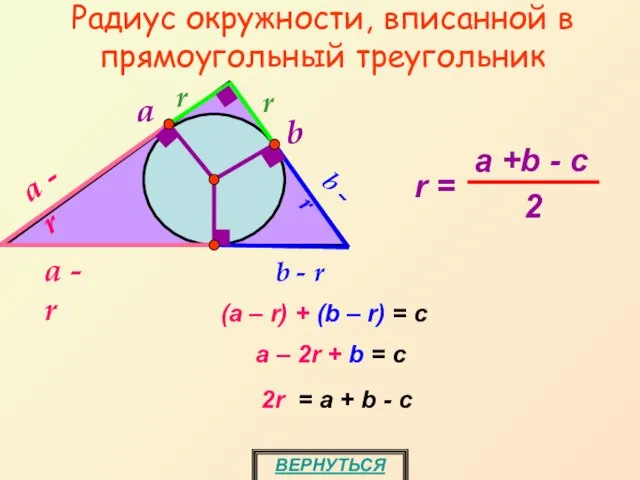
Радиус окружности, вписанной в прямоугольный треугольник
r
r
b - r
b - r
b
a
a - r
a - r
(a – r) + (b – r) = с
a – 2r + b = с
2r = а + b - с
ВЕРНУТЬСЯ

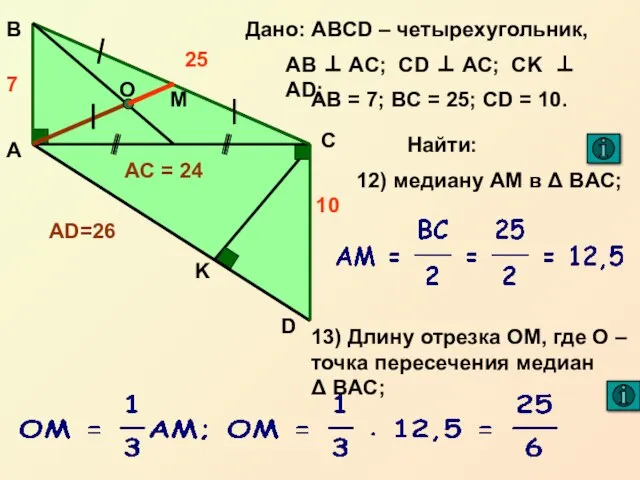
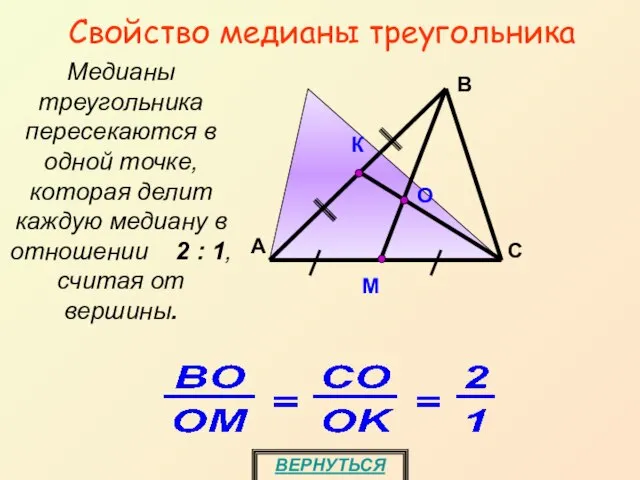
Свойство медианы треугольника
ВЕРНУТЬСЯ
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
M
А
С
В
О
К