ПУТЕШЕСТВИЕ на планету

Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
Мы в поход отправляемся смело
В мир загадок и сложных задач.
Не беда, что идти далеко.
Не боимся, что путь будет труден.
Достижения крупные людям
Никогда не давались легко.
В наше время, чтобы строить
И машиной управлять,
Прежде нужно уже в школе
Математику узнать.
На войне ли современной,
В годы ль мирного труда,
При расчетах непременно
Математика нужна.

Операция "Компьютер"

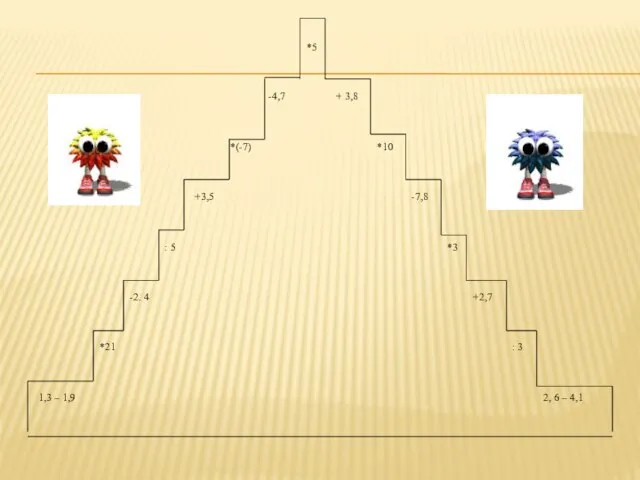
ПРОВЕРЯЕМ БЛОК ПАМЯТИ:
Проверьте
1) - 3,23 - 8 = 11, 23
2) 48 : (-5) = 9,6
3) 24,23 – (- 2,2) = 22,03
4) - 25 * ( -8) = 250
5) -4, 5 + 9, 4 = - 4,9
6) -11,9 – 1,2 = - 12,1
7) – 10 * (- 18) = - 18

ВЫЧИСЛИТЕ:
1) – 5, 8 - 4, 2
2) - 19,6 + 2,5
3) – 24 : (-5)
4) 18 * (- 3)

ПРОКОНТРОЛИРУЙТЕ РАБОТУ КОМПЬЮТЕРА:
а) 8 – 70 б) – 19 + 100 в) – 18 - 46
-19 : (-3) : 16
: 3 - 13 - 77
* (-2) + 6 : (-3)

РАКЕТА

ВОЛШЕБНЫЙ САД

1) Как умножить два числа с разными знаками.
2) Как сложить два отрицательных числа.
3) Как разделить два отрицательных числа.
4) По какому правилу выполняется вычитание чисел.
5) Как сложить два числа с разными знаками.
6) Какие числа называют противоположными.

МУЗЕЙ
истории
рациональных
чисел

С рациональными числами люди знакомились постепенно, вна­чале при счете предметов возникли натуральные числа. На первых порах их было немного. Так, еще недавно у туземцев островов в Торресовом проливе (отделяю­щем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа - урапун» (три), «оказа - оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много».
Величайший древнегреческий математик и физик Архимед (287—212 до н. э.) придумал способ описания гро­мадных чисел. Самое большое число, которое умел назы­вать Архимед, было настолько велико, что для его цифро­вой записи понадобилась бы лента в две тысячи раз длин­нее, чем расстояние от Земли до Солнца.
При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»?

Однако, несмотря на такие сомнения и недоумения, правила умножения и деления положительных и отрицательных чисел были предложены в III в. греческим матема­тиком Диофантом (в виде: «Вычитаемое, умноженное на прибавляемое, дает вычи­таемое; вычитаемое на вычитаемое дает прибавляемое» и т. д.), а позже индийский математик Бхаскара (XII в.) выразил те же правила в понятиях «имущество», «долг» («Произведение двух имуществ или двух долгов есть имущество; произведение иму­щества и долга есть долг». То же правило и при делении).
Было установлено, что свойства действий над отрицательными числами те же, что и над положительными (например, сложение и умножение обладают переместительным свойством). И наконец, с начала XIX в. отрицательные числа стали равноправными с положительными.
В дальнейшем в математике появились новые числа — иррациональные, комплексные и другие. О них вы узнаете в старших классах.

Город Законов

Вычислите:
1) – 13 – 15 + 9 - 17
2) 20 – 14 – 13 + 7
3) ( -2) * ( -24,3) * ( -5)
4) ( - 5) * ( - 4) * 31
5) 0,25 * ( - 4) * ( - 8)

Водопад упрощений

1)Упростите выражение
11а – 5а + 7а – 9а
2) Упростите выражение
10х – 4х + х – 6х + 5
и найдите его значение при х = - 15.

Озеро Неизвестности

Решите уравнение
15,7 + х = 12,3
9,7 – у = 12, 4
7,2 : а = - 1,2
2 z – 3 = -5

ЗАДАНИЕ НА ДОМ
№ 1250 (г,д,е)
№ 1270
№ 1274

МОЛОДЦЫ!