Рекурсивные алгоритмы ЕГЭ-2017 по информатике Задание 11

Теория
Рекурсия вокруг нас
Рекурсия в математике
Программирование
Задачи на закрепление
Список использованной литературы
Содержание

Реку́рсия (RECURCIО - возвращение) — определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя.
Теория
Рекурсивным называется любой объект, который частично определяется через себя.

Что нужно знать:
Рекурсия может быть прямой и косвенной.
Рекурсия – это приём, позволяющий свести исходную задачу к одной или нескольким более простым задачам того же типа.
Чтобы определить рекурсию, нужно задать:
-условие остановки рекурсии
-рекуррентную формулу
Любую рекурсивную процедуру можно запрограммировать с помощью цикла
Рекурсия позволяет заменить цикл и в некоторых сложных задачах делает решение более понятным, хотя часто менее эффективным.
Теория

Рекурсия может быть прямой и косвенной.
В случае прямой рекурсии вызов функцией самой себя делается непосредственно в этой же функции
procedure F(n: integer);
begin
writeln(n);
if n > 1 then begin
F(n-1);
F(n-3)
end
end;
end;
Теория

Косвенная рекурсия создаётся за счёт вызова
данной функции из какой-либо другой функции,
которая сама вызывалась из данной функции.
function F(n: integer): integer;
begin
if n > 2 then F := F(n - 1) + G(n - 2)
else F := 1;
end;
function G(n: integer): integer;
begin
if n > 2 then G := G(n - 1) + F(n - 2)
else G := 1;
end;
Теория

Уроборос – змей, кусающий свой собственный хвост. Это древний символ бесконечности Вселенной и времени, круговорота жизни, отождествляемых с рекурсией.
Рекурсия вокруг нас…
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Классическим примером конечной рекурсии является русская матрешка.

Рассказ из С.Лева «Кибериады» о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей. (бесконечная рекурсия - каждая новая машина строила себе подобную).
Рекурсия вокруг нас…
Н.В. Гоголь в повести «Портрет» описывает сон художника Черткова (сон третьего уровня рекурсии). Проснувшись от этого сна Чертков попадает на второй уровень рекурсии – во второй сон. Проснувшись от второго сна, он попадает в первый сон, от которого тоже придется проснуться.
"Мастер и Маргарита" - один из наиболее ярких рекурсивных романов.
Тема Иешуа и Пилата рекурсивно вызывается из темы Мастера и Маргариты. Кроме того, здесь так же используется прием "книга в книге". Мастер пишет роман об Иешуа и Пилате, текст которого сливается с текстом книги "Мастер и Маргарита".

Первым романом, удивившим читателей приемом рекурсии, был "Дон Кихот". Сервантес все время пытался смешивать два мира: мир читателя и мир книги. У Сервантеса главный процесс не просто книга, но книга плюс читатель. В шестой главе цирюльник, осматривая библиотеку Дон Кихота, находит книгу Сервантеса и высказывает суждения о писателе. Вымысел Сервантеса рассуждает о нем. В начале девятой главы сообщается, что роман переведен с арабского и что Сервантес купил его на рынке. Наконец, во второй части романа персонажи уже прочли первую часть.
Рекурсия вокруг нас…
Элементы использования рекурсии находим еще раньше у Шекспира. Гамлет ставит спектакль, где в упрощенном варианте описываются события трагедии.
В романее Л. Толстого «Война и мир» рекурсия отражает прошлое в настоящем и будущем.

Рекурсия вокруг нас…
У попа была собака, он её любил
Она съела кусок мяса, он её убил
В землю закопал,
Надпись написал:
«У попа была собака, он её любил
Она съела кусок мяса, он её убил
В землю закопал,
Надпись написал:
Р. Бернс «Дом, который построил Джек» в переводе
С. Маршака
Вот дом,
Который построил Джек.
А это пшеница,
Которая в темном чулане хранится
В доме,
Который построил Джек
А это веселая птица-синица,
Которая часто ворует пшеницу,
Которая в темном чулане хранится.

Рекурсия вокруг нас…
А. Блока
Ночь, улица, фонарь, аптека.
Бессмысленный и тусклый свет.
Живи еще хоть четверть века –
Все будет так. Исхода нет.
Умрешь – начнешь опять сначала,
И повторится все, как встарь:
Ночь, ледяная рябь канала,
Аптека, улица, фонарь.

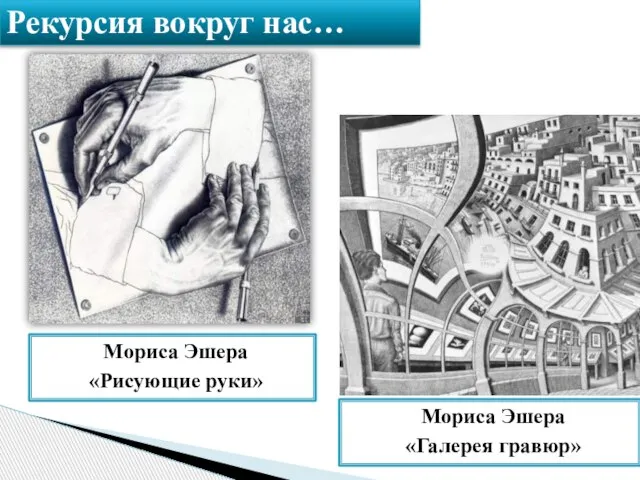
Мориса Эшера
«Рисующие руки»
Мориса Эшера
«Галерея гравюр»
Рекурсия вокруг нас…

Рекурсия вокруг нас…
Фрактал
"Треугольник Серпинского"
Эйфелева Башня в Париже
Исторический музей в Москве

Рекурсия вокруг нас…
Дерево состоит из веток. Ветка в свою очередь состоит из более маленьких веточек. Каждая ветка повторяет дерево.
Реки образуются из впадающих в них рек.
Чешуя шишек и семена некоторых цветов (например, подсолнечника) расположены пересекающимися
спиралевидными веерами, определяемыми соотношением чисел Фибоначчи.

Эффект Дросте - термин для изображения специфического вида рекурсивного изображения. Изображение включает уменьшенный собственный вариант самого себя. Этот более малый вариант после этого показывает даже более малый вариант себя, и так далее. Практически это продолжается пока разрешение изображения позволяет уменьшает размер. Термин был введен в честь Дросте, голландского какао.
Рекурсия вокруг нас…

Рекурсия вокруг нас…
Герб Российской Федерации
является рекурсивно-определённым графическим объектом: в правой лапе изображённого на нём двуглавого орла зажат скипетр, который венчается уменьшенной копией герба. Так как на этом гербе в правой лапе орла также находится скипетр, получается бесконечная рекурсия.

Рекурсия в математике
1) Арифметическая прогрессия:
а)а1=а0;
б) аn=аn-1+d.
2) Геометрическая прогрессия:
а) а1=а0;
б) аn=а n-1*q.

Рекурсия в математике
3) Факториал
an=n! n!=1*2*3*4*5*б*...*n.
а)а1=1;
б) аn=n*аn-1.
4) Числа Фибоначчи.
x1=x2=1
xn=xn-1+xn-2 при n > 2 Каждый элемент ряда Фибоначчи является суммой двух предшествующих элементов, т.е. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…

Программирование
Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе.
В программировании рекурсия — вызов функции из неё же самой, непосредственно или через другие функции, например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

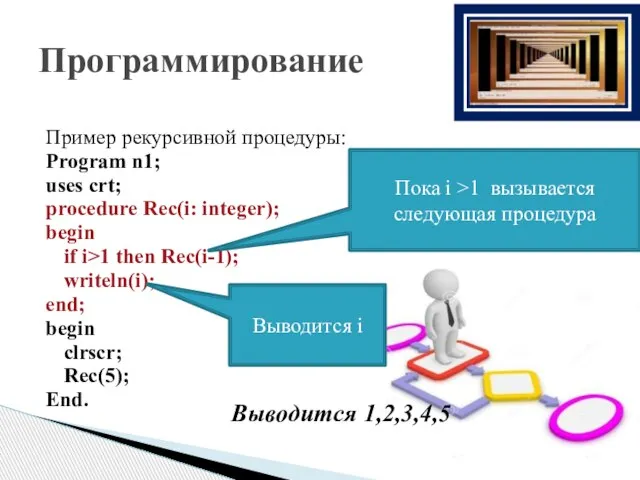
В языке программирования Pascal
рекурсивностью могут обладать как
функции, так и процедуры.
Примеры рекурсивной процедуры.
Общая форма записи:
Procedure Rec (a:integer);
Begin
If a>0 Then Rec(a-1);
Writeln(a);
End;
Программирование
Важно!
Выполнение рекурсивного алгоритма можно представить следующим образом:
каждый рекурсивный вызов процедуры F порождает в памяти компьютера новую копию этой процедуры и запускает ее на выполнение со своими значениями входных параметров.
После того как процедура F завершила работу, выполнение программы продолжается со следующего оператора после вызова F.

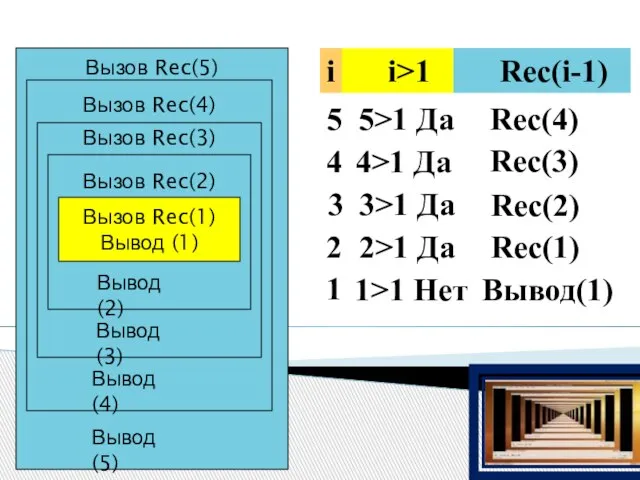
Пример рекурсивной процедуры:
Program n1;
uses crt;
procedure Rec(i: integer);
begin
if i>1 then Rec(i-1);
writeln(i);
end;
begin
clrscr;
Rec(5);
End.
Программирование
Выводится 1,2,3,4,5
Пока i >1 вызывается следующая процедура
Выводится i

Вызов Rec(5)
Вызов Rec(4)
Вызов Rec(3)
Вызов Rec(2)
Вызов Rec(1)
Вывод (1)
Вывод (2)
Вывод (3)
Вывод (4)
Вывод (5)
i>1
i
Rec(i-1)
5
4
3
2
1
5>1 Да
4>1 Да
3>1 Да
2>1 Да
1>1 Нет
Rec(4)
Rec(3)
Rec(2)
Rec(1)
Вывод(1)

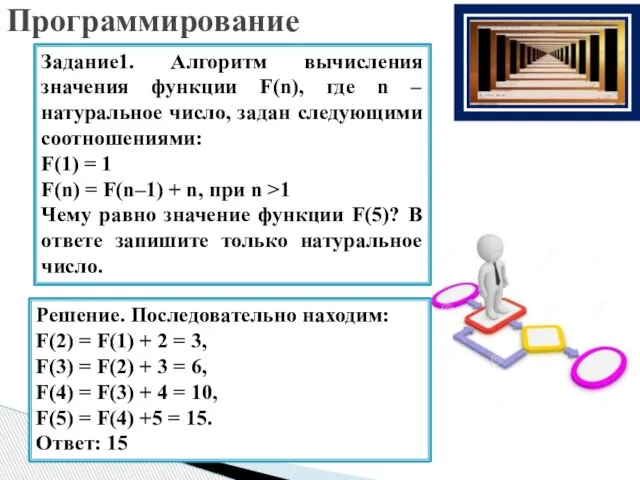
Программирование
Задание1. Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = F(n–1) + n, при n >1
Чему равно значение функции F(5)? В ответе запишите только натуральное число.
Решение. Последовательно находим:
F(2) = F(1) + 2 = 3,
F(3) = F(2) + 3 = 6,
F(4) = F(3) + 4 = 10,
F(5) = F(4) +5 = 15.
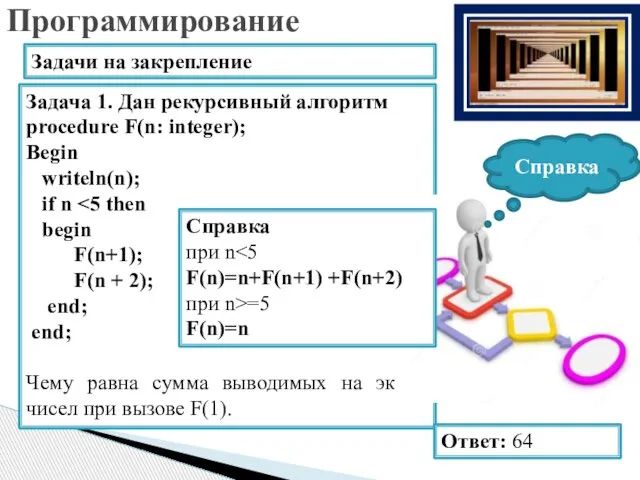
Ответ: 15

Задание 2. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n < 5 then begin
F(n + 1);
F(n + 3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).
Программирование
Складывая все эти числа, получаем 49

Задание 3. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n < 6 then begin
F(n+2);
F(n*3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).
Программирование
Складывая все эти числа, получаем 79

Задание 4. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n < 3 then write('*')
else begin
F(n-1);
F(n-2);
F(n-2)
end;
end;
Сколько звездочек напечатает эта процедура при вызове F(6)? В ответе запишите только целое число.
Программирование
Решение:
Найдем значение процедуры:
F(6)=F(5)+2*F(4)
F(5)=F(4)+2*F(3)
F(4)=F(3)+2*F(2)
F(3)=F(2)+2*F(0)=F(2)+2*1=F(2)+2
F(2)=1
Следовательно:
F(3)=1+2=3
F(4)=3+2*1=5
F(5)=5+2*3=11
F(6)=11+2*5=21

Задание 5. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n <=4 then
begin
F(n*2);
F(n +1);
end
end;
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(2)?
Программирование
F(2)
F(4)
F(3)
F(8)
F(5)
F(4)
F(6)
F(8)
F(5)
8+4+5+2+3+4+6+8+5=45
!
Построенное дерево позволяет ответить на более сложный вопрос: «Что напечатает программа?»
Выписав значения узлов в порядке построения, получим:
2 4 8 5 3 6 4 8 5
Результат работы программы при ином расположении оператора печати n, в общем случае, отличается от данного.

Задание 5. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n <=4 then
begin
F(n*2);
F(n +1);
end
end;
Чему равна сумма всех чисел, напечатанных на экране при выgолнении вызова F(2)?
Программирование
Решение (II способ):
При n<=4
F(n)=n+F(2n)+F(n+1)
При n>4
F(8)=8; F(7)=7; F(6)=6; F(5)=5
Найдем значение процедуры:
F(4)=4 +F(2*4)+F(4+1)=4+F(8)+F(5)=
=4+8+5=17
F(3)=3 +F(2*3)+F(3+1)=3+F(6)+F(4)=
=3+6+17=26
F(2)=2 +F(2*2)+F(2+1)=2+F(4)+F(3)=
=2+17+26=45

Задание 6. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n <=4 then
begin F(n*2);
F(n+1);
end;
write(n);
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(2).
Программирование
Решение:
при n<=4 F(n)=F(2n)+F(n+1)+n
при n>4 F(n)=n
Найдем значение процедуры:
F(2)=F(2*2)+F(2+1)+2=F(4)+F(3)+2
F(3)=F(2*3)+F(3+1)+3=F(6)+F(4)+3
F(4)=F(2*4)+F(4+1)+4=F(8)+F(5)+4
F(2)=F(8)+F(5)+4+F(6)+F(8)+F(5)+4+3+2
Ответ:
8,5,4,6,8,5,4,3,2

Задание 7. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n <=4 then
begin F(n*2);
write(n);
F(n+1);
end;
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(2).
Программирование
Решение:
при n<=4 F(n)=F(2n)+n +F(n+1)
при n>4 F(n)= «не печатает!»
Найдем значение процедуры:
F(2)=F(2*2)+2+F(2+1)=F(4)+2+F(3)
F(3)=F(2*3)+3+F(3+1)=F(6)+3+F(4)
F(4)=F(2*4)+4+F(4+1)=F(8)+4+F(5)
F(2)=4+2+F(3)=4+2+3+F(4)=4+2+3+4
Ответ:
4,2,3,4

Задание 8. Дан рекурсивный алгоритм
procedure F(n: integer);
begin
if n >1 then
begin F(n-2);
write(n);
F(n div 2);
end;
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(6).
Программирование
Решение:
при n>1 F(n)=F(n-2)+n +F(n div 2)
при n<=1 F(n)= «не печатает!»
Найдем значение процедуры:
F(6)=F(6-2)+6+F(6 div 2)=F(4)+6+F(3)
F(4)=F(4-2)+4+F(4 div 2)=F(2)+4+F(2)
F(3)=F(3-2)+3+ F(3 div 2)=F(1)+3+F(1)
F(2)=F(2-2)+2+ F(2 div 2)=F(0)+2+F(1)
F(6)=F(2)+4+F(2)+6+F(3)= =F(2)+4+F(2)+6+3=2+4+2+6+3
Ответ:
2,4,2,6,3

Задание 9. Дан рекурсивный алгоритм
procedure F(n: integer);
Begin
write(n);
if n >1 then begin
F(n-2);
F(n div 2);
end;
end;
Укажите через запятую последовательность выводимых чисел, в том порядке, как их напечатает программа при выполнении вызова F(5).
Программирование
Решение:
при n>1 F(n)=n+F(n-2) +F(n div 2)
при n<=1 F(n)=n
Найдем значение процедуры:
F(5)=5+F(5-2)+F(5 div 2)=5+F(3)+F(2)
F(3)=3+F(3-2)+F(3 div 2)=3+F(1)+F(1)
F(2)=2+F(2-2)+F(2 div 2)=2+F(0)+F(1)
Получим:
F(2)=2+0+1
F(3)=3+1+1
F(5)=5+3+1+1+2+0+1
Ответ: 5,3,1,1,2,0,1

Задание 10. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(‘*’);
if n >0 then F(n-2) else G(n);
end;
procedure G(n: integer);
Begin
write(‘**’); if n >1 then F(n-3);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении F(20)?
Программирование
Решение:
при n>10 F(n)=‘*’+F(n-2)
при n<=10 F(n)=‘**’ +F(n-3)
при n<=1 G(n)=‘**’
Найдем значение процедуры:
F(20)=* +F(18)
F(18)=* +F(16)
F(16)=* +F(14)
F(14)=* +F(12)
F(12)=* +F(10)
F(10)=* + ** +F(7)
F(7)=* + ** +F(4)
F(4)=* + ** +F(1)
F(1)=* + **
Ответ: 17
F(1)=3
F(4)=3+3=6
F(7)=3+6=9
F(10)=3+9=12
F(12)=1+12=13
F(14)=1+13=14
F(16)=1+14=15
F(18)=1+15=16
F(20)=1+16=17

Задача 1. Дан рекурсивный алгоритм
procedure F(n: integer);
Begin
writeln(n);
if n <5 then begin
F(n+1);
F(n + 2);
end;
end;
Чему равна сумма выводимых на экран чисел при вызове F(1).
Программирование
Ответ: 64
Задачи на закрепление
Справка
при n<5
F(n)=n+F(n+1) +F(n+2)
при n>=5
F(n)=n
Справка

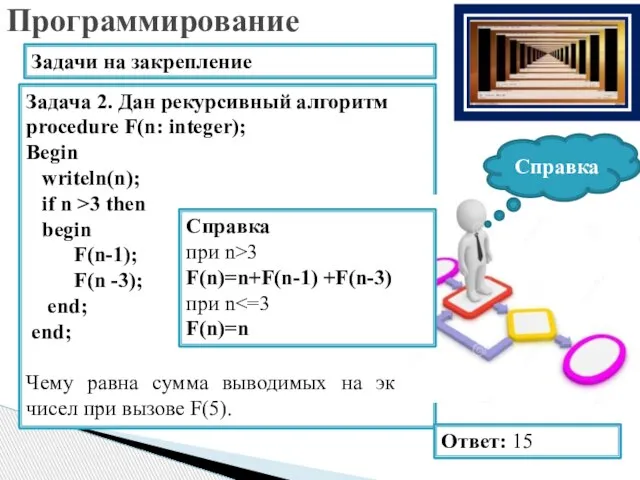
Задача 2. Дан рекурсивный алгоритм
procedure F(n: integer);
Begin
writeln(n);
if n >3 then begin
F(n-1);
F(n -3);
end;
end;
Чему равна сумма выводимых на экран чисел при вызове F(5).
Программирование
Ответ: 15
Задачи на закрепление
Справка
при n>3
F(n)=n+F(n-1) +F(n-3)
при n<=3
F(n)=n
Справка

Программирование
Задачи на закрепление
Задача 3. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(‘*’);
if n >10 then F(n-2) else G(n);
end;
procedure G(n: integer);
Begin
write(‘**’); if n >0 then F(n-3);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении F(18)?
Ответ: 19

Программирование
Задачи на закрепление
Задача 4. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(‘*’);
if n >=2 then F(n-2) else G(n);
end;
procedure G(n: integer);
Begin
write(‘**’); if n >1 then F(n-3);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении F(22)?
Ответ: 18

Программирование
Задачи на закрепление
Задача 5. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(n);
if n mod 2 =0 then F(n div 2)
else G((n-1) div 2);
end;
procedure G(n: integer);
Begin
write(n); if n >0 then F(n);
end;
Какова сумма чисел, напечатанных на экране при выполнении вызова F(17)?
Ответ: 40

Программирование
Задачи на закрепление
Задача 6. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(n mod 2);
if n mod 2 =0 then F(n div 2)
else G((n-1) div 2);
end;
procedure G(n: integer);
Begin
write(n); if n >0 then F(n);
end;
Какова сумма чисел, напечатанных на экране при выполнении вызова F(19)?
Ответ: 16

Программирование
Задачи на закрепление
Задача 7. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
write(n mod 2);
if n mod 2 =0 then F(n div 2)
else G((n-1) div 2);
end;
procedure G(n: integer);
Begin
write(n mod 2); if n >0 then F(n);
end;
Сколько нулей будет выведено на экране при выполнении вызова F(21)?
Ответ: 5

Программирование
Задачи на закрепление
Задача 8. Даны два рекурсивных алгоритма
procedure F(n: integer); forward;
procedure G(n: integer); forward
procedure F(n: integer);
Begin
if n mod 5 =0 then G(n -5)
else F(n-3);
end;
procedure G(n: integer);
Begin
write(‘*’); if n >0 then F(n-1);
end;
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(51)?
Ответ: 4

Список использованной литературы
Крылов С.С ЕГЭ 2017. Информатика Тематические тестовые задания/С.С. Крылов, Д.М. Ушаков.-М.:Издательство «Экзамен», 2017
Крылов С.С, Чуркина Т.Е. ЕГЭ. Информатика и ИКТ: типовые экзаменационные варианты: 20 вариантов. -М.:Издательство «Национальное образование», 2017
Бражникова О.В. Рекурсия. Рекурсивные алгоритмы http://easyen.ru
Исламов Р.Г. «Рекурсивные алгоритмы». Разбор заданий №11 ЕГЭ по информатике и ИКТ
Коротун О.В. Рекурсивные алгоритмы. Задание 11 ЕГЭ. http://proteacher.ru/2015/01/10/Rekursivnye_algoritmy_1420913156_12749.pptx
Юдин А.Б. Рекрусия http://www.uchportal.ru/load/18-1-0-55354

Слайд 1, 2 http://arxweb.net/pictures/raznoe/recursia.jpeg
Слайд 3-7,17,18,20-36, 44 https://upload.wikimedia.org/wikipedia/commons/b/b3/Screenshot_Recursion_via_vlc.png
Слайд 3 http://lols.ru/uploads/posts/2011-07/1309983680_1309964j.jpg
Слайд 7 Змей http://ezolan.ru/image/cache/data/Talisman/smola/kumirnica/95-500x500.jpg
Зеркала http://cdn01.ru/files/users/images/92/44/92443e52bffa0b4f29b8075eb6a50193.jpg
Матрешки https://image.jimcdn.com/app/cms/image/transf/none/path/seb6ba021dbaf218c/image/i0b5fd1e834074150/version/1418029668/image.jpg
Слайд 8 Лем http://tomuz.ru/uploads/images/l/e/m/lem_stanislav_kiberiada_01_skazki_robotov.jpg
Портрет https://fs00.infourok.ru/images/doc/233/91173/2/img4.jpg
Мастер и Маргарита http://biblus.ru/pics/7/f/f/1005817671.jpg
Слайд 9
Гамлет http://botinok.co.il/sites/default/files/images/c44e9d5e0c2582fb3bfd9c60e1e36ea5_smoktunovskiy_gamlet.jpg
Дон Кихот https://upload.wikimedia.org/wikipedia/commons/thumb/a/ac/Honoré_Daumier_017_%28Don_Quixote%29.jpg/416px-Honoré_Daumier_017_%28Don_Quixote%29.jpg
Война и мир http://www.abbyreader.ru/pic/fa649070809c3dfb3fa768b4d8fd528a.jpg
Слайд 10
Поп http://cdn01.ru/files/users/images/e4/31/e4311658d876f53c249807107fc54648.jpg
Джек http://s-marshak.ru/books/d/d27/d27_02.jpg
Слайд 11 https://lh3.googleusercontent.com/-SqgOCQ0nNsk/TKnKgCfpcKI/AAAAAAAAHe4/1E4isRsTzeEJBdFNBeDLDEp_RRH-VHnEgCHM/s800/0_2910a_67b4058a_XL.jpg
Интернет-ресурсы