Технологический расчет баромембранных установок

Задача:
определение рабочей поверхности мембран, всех потоков и концентраций входящих в них веществ
Модель Идеального Вытеснения
концентрации и скорости постоянны в любой точке поперечного сечения напорного канала,
продольное перемешивание отсутствует,
концентрация плавно изменяется от входа в аппарате до выхода из него,
пермеат отводится строго перпендикулярно потоку разделяемого раствора.
процесс идёт при постоянном давлении и температуре.
х2

х2=g(x1); (1)
G=f(x1) (2)
x1— массовая доля растворённого вещества в разделяемом растворе в произвольном сечении аппарата,
х2 — массовая доля растворённого вещества в пермеате в том же сечении.
Уравнения материального баланса
Lн = Wоб + Lк; (3)
(4)
Lн, Lк — соответственно, массовые расходы исходного раствора и концентрата,
Wоб — массовый расход пермеата со всего аппарата,
— массовая доля растворённого вещества в пермеате,
x1н, x1к — соответственно, массовые доли растворённого вещества в исходном растворе и концентрате.
х2

Задано:
расход исходного раствора и его концентрация
задаётся x1к
L — массовый расход разделяемого раствора в выбранном произвольном сечении,
x — массовая доля растворённого вещества в разделяемом растворе в этом сечении,
W — массовый расход пермеата на участке от входа в аппарат до рассматриваемого сечения,
— массовая доля вещества в пермеате, характеризуемом расходом W, т.е. средняя концентрация на участке от входа в аппарат до рассматриваемого сечения.
Пусть на элементе поверхности dF в рассматриваемом произвольном сечении образуется пермеат с расходом dW и концентрацией x2 растворённого вещества, и за счёт этого изменение его расхода с пермеатом составляет:
х2
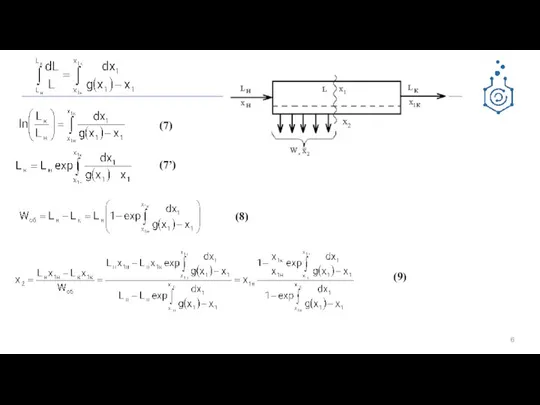
(5)

Образование пермеата сопровождается соответствующей убылью расхода разделяемого раствора:
dW=-dL
Преобразуем выражения (5)
- dL⋅x2 = - d(L⋅x1)
В соответствии с (1) х2=g(x1)
=g(x1)
(6)
х2

(7)
(7’)
(8)
(9)
х2

Частный случай:
селективность ϕ сохраняется постоянной при изменении концентрации растворённого вещества
x2 = g(x1) = x1(1 — ϕ)
(10)

Частный случай:
Подставим (10) в (7), (8) и (9)
(11!)
(12)
(13)
Домашнее задание:
получить формулу, позволяющую определять селективность мембраны, необходимую для концентрирования раствора от х1н до х1к при условии, чтобы концентрация растворённого вещества в пермеате не превышала некоторой величины

Рабочая поверхность мембран
х2
Расход пермеата в произвольном сечении dF:
dW=G⋅dF
dW=-dL
(6)
G=f(x1) (2)

L – некая функция
х2

Проинтегрируем по всей рабочей поверхности:
(14)
Частный случай:
селективность ϕ сохраняется постоянной при изменении концентрации растворённого вещества
удельная производительность линейно снижается в соответствии с уравнением: G=G0-cx1
(15)

Частный случай ϕ≥ 0,9 :
(16)
g(x1н) < < x1н < x1к

Учёт в расчётах условий в реальных аппаратах:
1. Постоянство температуры
Оправдано.
Селективность и удельную производительность при среднем значении температуры
2. Постоянство давления
Менее оправдано. Гидравлическое сопротивление
Селективность и удельную производительность при среднем значении перепада рабочего давления или при минимальном в выходном сечении аппарата
3. Модель Идеального Вытеснения
Концентрационная поляризация
Корректировка в зависимости G=f(х1) и х2=g(x1)

Метод последовательных приближений:
Первое приближение КП=1
Выбрать:
тип баромембранного процесса;
вид мембран и аппаратов;
рабочее давление и температура.
Рассчитать:
величины расходов потоков и их концентраций,
необходимую рабочую поверхность мембран.
Распределить:
аппараты по секциям
Определить гидродинамические условия:
коэффициент массоотдачи растворённого вещества от поверхности мембраны в ядро потока разделяемого раствора с использованием известных критериальных уравнений.
Рассчиттать КП и внести корректировку в зависимости G=f(х1) и х2=g(x1)

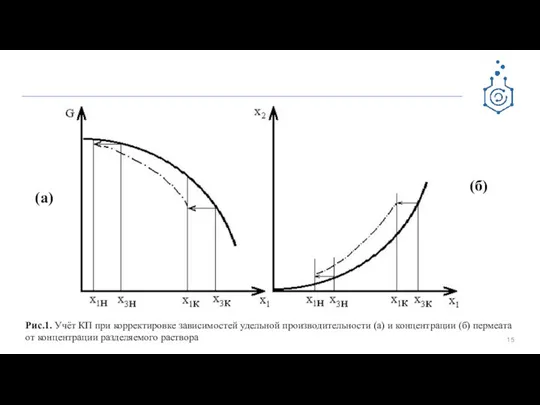
Рис.1. Учёт КП при корректировке зависимостей удельной производительности (а) и концентрации (б) пермеата от концентрации разделяемого раствора
(а)
(б)

Частный случай
G = G0 - сх1
G = G0 — ссрх1
сср= (сн + ск)/2
Селективность мембраны не зависит от концентрации
β —коэффициент массоотдачи,
G — удельная производительность мембраны,
рассчитанные по уравнениям переноса с учётом КП

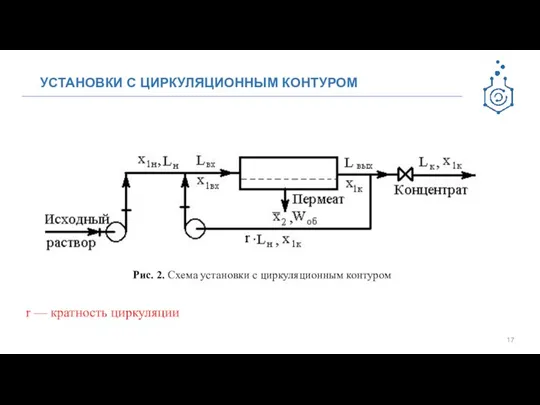
УСТАНОВКИ С ЦИРКУЛЯЦИОННЫМ КОНТУРОМ
Рис. 2. Схема установки с циркуляционным контуром
r — кратность циркуляции

Модель Идеального Вытеснения:
Уравнения материального баланса
Lн = Wоб + Lк; (3)
(4)
три новых переменных: Lвх, Lвых, x1вх
кратность циркуляции r мы считаем заданной
Lн⋅x1н + r⋅Lн⋅х1к = Lвх⋅х1вх (19)
(17)
(18)

ДОМАШНЕЕ ЗАДАНИЕ:
Произвести аналогичные МИВ без рециркуляции преобразования и получить расчётные выражения:
(20)
(21)
(22)
(23)
(24)

Частный случай:
селективность ϕ сохраняется постоянной при изменении концентрации растворённого вещества
(26)
(25)
(27)
(28)
удельная производительность линейно снижается с увеличением концентрации
(29)
Учитывать КП!!!

Модель Идеального Смешения:
(теоретически — при r →∞, практически — r превышает несколько десятков)
G = f(x1к) = const;
x2 = g(x1к) = const= ;
Уравнения материального баланса:
Lвх = Lвых = r⋅Lн
(30)
(31)
(32)
(33)
Учитывать КП!!!
G = f(x1к⋅КП) = const
х2=g(x1к⋅КП) = const=