Теория электрической связи

*
Лекция 1. Введение
Число пользователей мобильной связи (в млн.)
140 (1996 г.) 205 (1997 г.) 290 (1998 г.)
380 (1999 г.) 500 (2000 г.) 680 (2001 г.)
Страны с наибольшим удельным числом пользователей (на конец 20 века)
1. Финляндия. 2. Швеция. 3. Норвегия. 4. Дания
Первый стандарт беспроводного доступа в Интернет (стандарт 802.11 Wi-Fi (Wireless Fidelity)) на передачу данных со скоростью до 2 Мбит/с в диапазоне 2,4 ГГц ратифицирован в 1997 году
Стандарт 802.11b на передачу данных со скоростью до 11 Мбит/с в диапазоне 2,4 ГГц ратифицирован в 1999 году
Стандарт 802.11а ратифицирован в 1999 году и регламентирует скорость передачи данных до 54 Мбит/с в частотном диапазоне 5 ГГц

*
Основные концепции построения сотовых сетей
Особенности сотовой архитектуры:
- передатчики небольшой мощности
- небольшие зоны покрытия сотами
- повторное использование частот
- дробление сот для уменьшения мощности
управление передачей вызова (handoff)
Макросота ~ 35 км
Сота ~ 3-5 км
Микросота ~ 0.8-1 км
Пикосота ~ 0.2 км

*
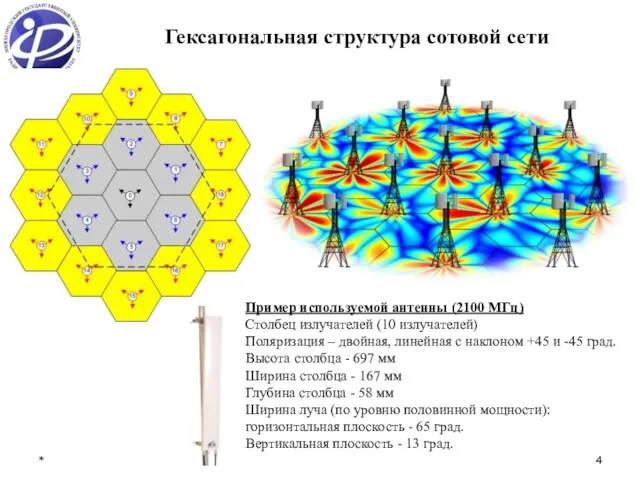
Гексагональная структура сотовой сети
Пример используемой антенны (2100 МГц)
Столбец излучателей (10 излучателей)
Поляризация – двойная, линейная с наклоном +45 и -45 град.
Высота столбца - 697 мм
Ширина столбца - 167 мм
Глубина столбца - 58 мм
Ширина луча (по уровню половинной мощности):
горизонтальная плоскость - 65 град.
Вертикальная плоскость - 13 град.

*
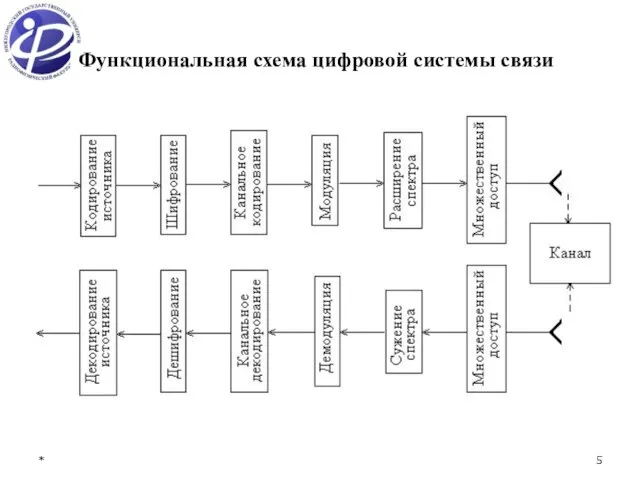
Функциональная схема цифровой системы связи

*
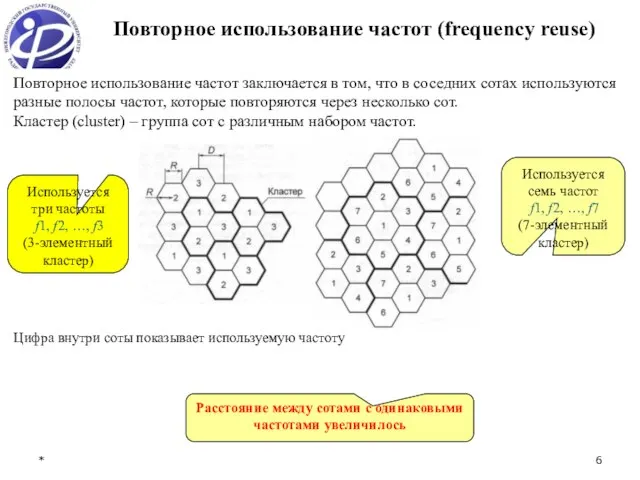
Повторное использование частот (frequency reuse)
Цифра внутри соты показывает используемую частоту
Используется три частоты f1, f2, …, f3
(3-элементный кластер)
Повторное использование частот заключается в том, что в соседних сотах используются разные полосы частот, которые повторяются через несколько сот.
Кластер (cluster) – группа сот с различным набором частот.
Используется семь частот
f1, f2, …, f7
(7-элементный кластер)
Расстояние между сотами с одинаковыми частотами увеличилось

*
Повторное использование частот
Отношение D/R=q называется коэффициентом уменьшения соканальных помех или коэффициентом соканального повторения.
Обратная величина C=1/N называется коэффициентом повторного использования частот
Расстояние между центрами сот с одинаковыми частотами
Расстояние между центрами сот с одинаковыми частотами,
R – радиус соты (радиус описанной окружности),
N – число сот в кластере.
N=3, D=3R. N=7, D=4,58R. N=19, D=7,55R.

*
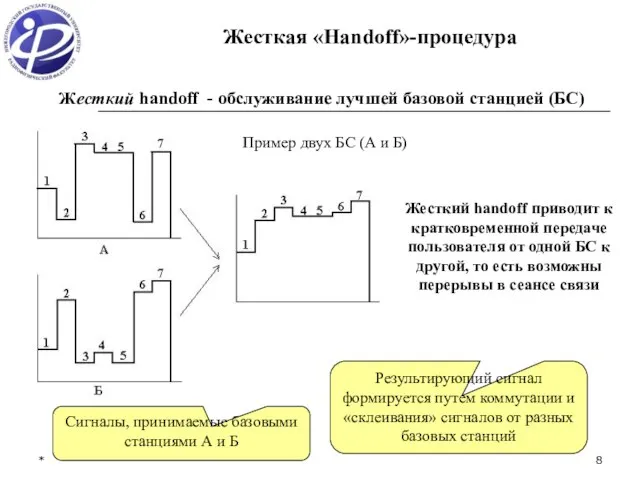
Жесткая «Handoff»-процедура
Жесткий handoff - обслуживание лучшей базовой станцией (БС)
Пример двух БС (А и Б)
Результирующий сигнал формируется путем коммутации и «склеивания» сигналов от разных базовых станций
Сигналы, принимаемые базовыми станциями А и Б
Жесткий handoff приводит к кратковременной передаче пользователя от одной БС к другой, то есть возможны перерывы в сеансе связи

*
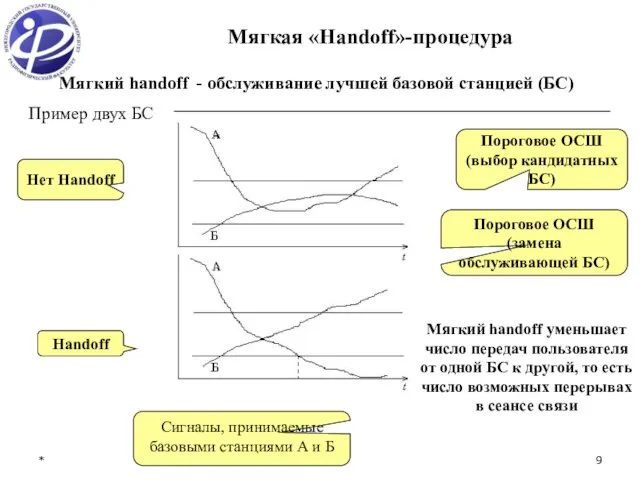
Мягкий handoff - обслуживание лучшей базовой станцией (БС)
Пример двух БС
Пороговое ОСШ (выбор кандидатных БС)
Пороговое ОСШ (замена обслуживающей БС)
Нет Handoff
Handoff
Сигналы, принимаемые базовыми станциями А и Б
Мягкий handoff уменьшает число передач пользователя от одной БС к другой, то есть число возможных перерывах в сеансе связи
Мягкая «Handoff»-процедура

*
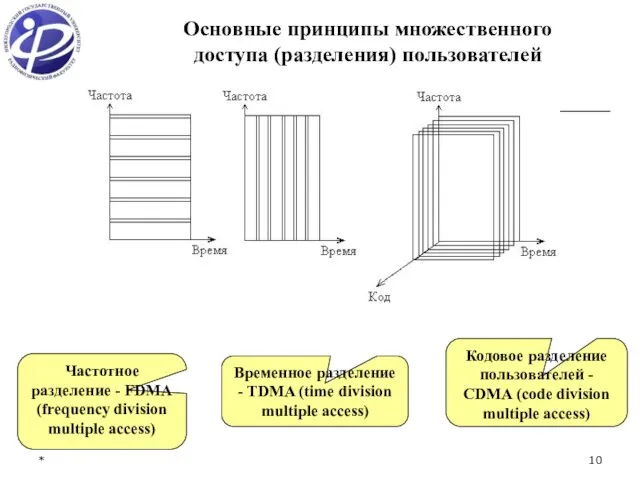
Частотное разделение - FDMA (frequency division multiple access)
Временное разделение - TDMA (time division multiple access)
Кодовое разделение пользователей - CDMA (code division multiple access)
Основные принципы множественного
доступа (разделения) пользователей

*
Частотное разделение пользователей
Разнос частотных каналов (GSM стандарт - 200Кгц)
М – число пользователей;
b – число бит в пакете;
Т – время передачи пакета.
1. Взаимное влияние каналов должно быть минимально возможным;
2. Время ожидания пакета для всех пользователей одинаково;
3. При замираниях в канале некоторые частотные каналы могут быть сильно ослаблены.
Скорость передачи данных R бит/сек (один пользователь).
М – число пользователей (число отдельных полос).
Длительность импульсов увеличивается в M раз, то есть все M пользователей одновременно передают информацию, но с уменьшенной скоростью R/M бит/сек.
Скорость передачи

*
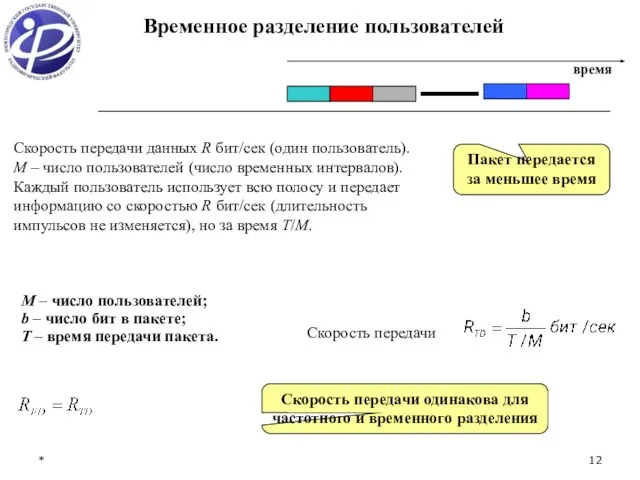
Временное разделение пользователей
М – число пользователей;
b – число бит в пакете;
Т – время передачи пакета.
Скорость передачи данных R бит/сек (один пользователь).
М – число пользователей (число временных интервалов).
Каждый пользователь использует всю полосу и передает информацию со скоростью R бит/сек (длительность импульсов не изменяется), но за время T/M.
Скорость передачи
Скорость передачи одинакова для частотного и временного разделения
Пакет передается за меньшее время
время

*
Производительность частотного и временного разделения пользователей
Временное разделение является более производительным, если учитывать время задержки пакета
Время задержки пакета состоит из среднего времени w ожидания пакета и из среднего времени τ передачи пакета
Частотное разделение - пакет передается без задержки
в течение T секунд
Временное разделение - пакет передается с задержкой в течение T/M секунд.
Время ожидания пакета для всех пользователей различно
Время задержки m-го пакета
Среднее время ожидания m-го пакета

*
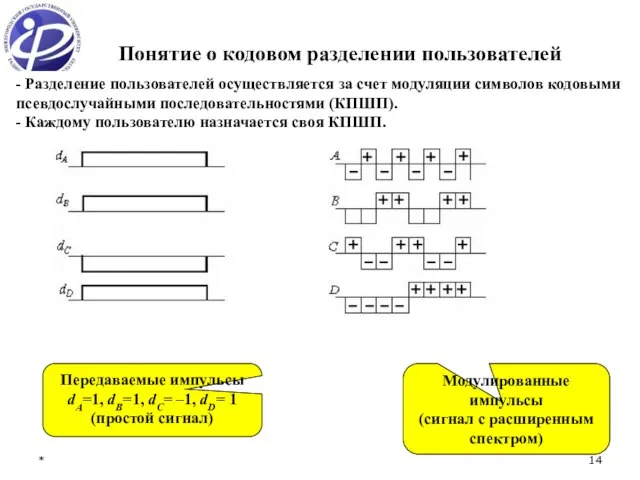
Понятие о кодовом разделении пользователей
- Разделение пользователей осуществляется за счет модуляции символов кодовыми псевдослучайными последовательностями (КПШП).
- Каждому пользователю назначается своя КПШП.
Модулированные импульсы
(сигнал с расширенным спектром)
Передаваемые импульсы dA=1, dB=1, dC= –1, dD= 1
(простой сигнал)

*
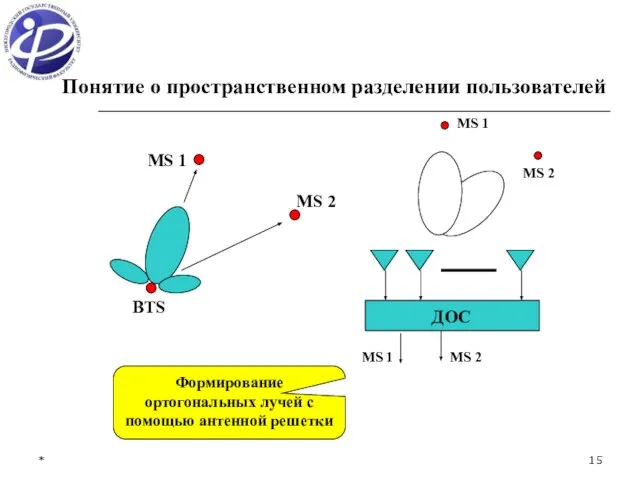
Понятие о пространственном разделении пользователей
ДОС
Формирование ортогональных лучей с помощью антенной решетки
MS 1
MS 2
MS 1
MS 2

*
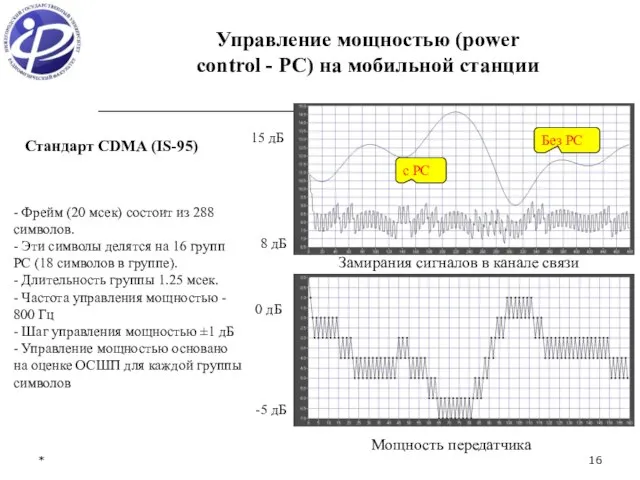
Замирания сигналов в канале связи
Мощность передатчика
- Фрейм (20 мсек) состоит из 288 символов.
- Эти символы делятся на 16 групп PC (18 символов в группе).
- Длительность группы 1.25 мсек.
- Частота управления мощностью - 800 Гц
- Шаг управления мощностью ±1 дБ
- Управление мощностью основано на оценке ОСШП для каждой группы символов
15 дБ
8 дБ
0 дБ
-5 дБ
Без РС
с РС
Стандарт CDMA (IS-95)
Управление мощностью (power
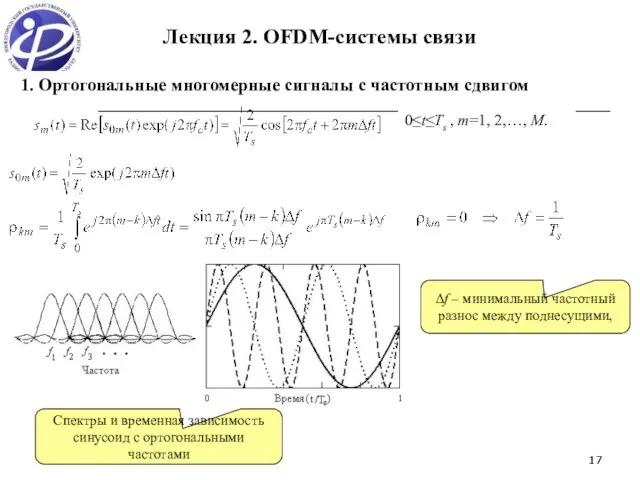
control - PC) на мобильной станции

*
*
0≤t≤Ts , m=1, 2,…, M.
Лекция 2. OFDM-системы связи
Спектры и временная зависимость синусоид с ортогональными частотами
Δf – минимальный частотный разнос между поднесущими,
1. Ортогональные многомерные сигналы с частотным сдвигом

*
*
dk – информационный символ, передаваемый на k–й поднесущей,
n – дискретное время, NF – число точек БПФ.
2. Формирование OFDM-сигнала
Передаваемый узкополосный сигнал
(n – дискретное время, NF – размерность БПФ)
3. Прием OFDM-сигнала
Принятый низкочастотный сигнал
z(n) – гауссов собственный шум приемника с нулевым средним и дисперсией
Приемник выполняет прямое БПФ

*
*
Hm – коэффициент передачи многолучевого канала на m-й поднесущей

*
*
ОСШ на m–й поднесущей

*
*
*
*
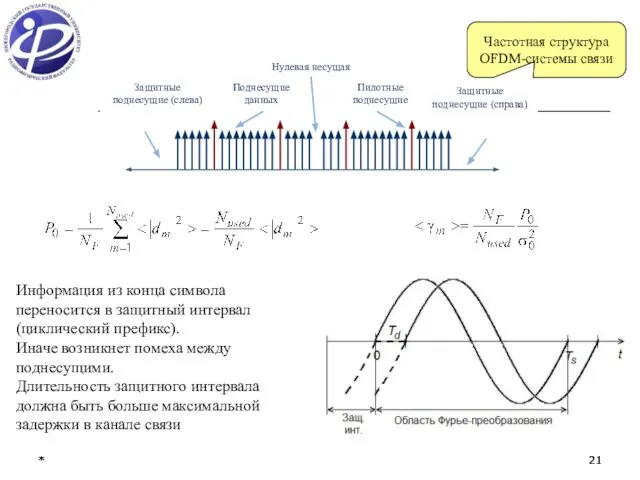
Частотная структура OFDM-системы связи
Информация из конца символа переносится в защитный интервал (циклический префикс).
Иначе возникнет помеха между поднесущими.
Длительность защитного интервала должна быть больше максимальной задержки в канале связи

*
*
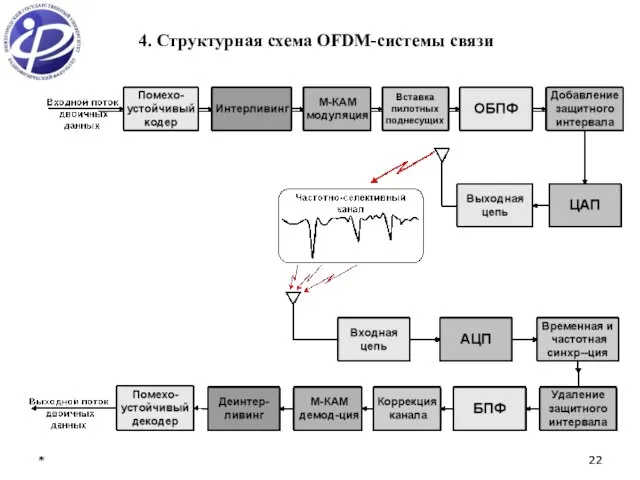
4. Структурная схема OFDM-системы связи

*
Коррекция канала или эквализация
Вход эквалайзера – выход блока БПФ
1. Простейший эквалайзер
Выход эквалайзера
Если на некоторых частотах коэффициент передачи канала неограниченно уменьшается (например, на m-й поднесущей Hm<< 1), то дисперсия шумовой составляющей на этой частоте может неограниченно увеличиваться. Это плохо.
2. Эквализация по минимуму среднеквадратической ошибки
Функционал среднеквадратической ошибки
Задача эквалайзера – восстановить спектр переданного сигнала, искаженного в частотно-селективном пространственном канале
f m – коэффициент передачи эквалайзера на m-ой частоте

*
*
- совпадение с простейшим эквалайзером
Т.о. сигнал ошибки эквалайзера ортогонален входному сигналу
Коэффициент передачи эквалайзера на m-ой частоте
Если на некоторых частотах коэффициент передачи канала неограниченно уменьшается (например, на m-й поднесущей Hm<< 1), то дисперсия шумовой составляющей на этой частоте не может неограниченно увеличиваться. Это хорошо.

*
*
5. Пропускная способность OFDM-системы
Каждый кластер (фрейм) кодируется и декодируется независимо.
Каждый кластер (фрейм) характеризуется:
Ns – число поднесущих; Nt – число OFDM-символов; Np – число пилотных поднесущих, kb – уровень модуляции (битовая загрузка символа), Rc – скорость кода.
ПС (ОСШ>>1) равна ширине полосы, используемой для передачи данных
(бит/сек)
(бит)
(бит/сек)

*
*
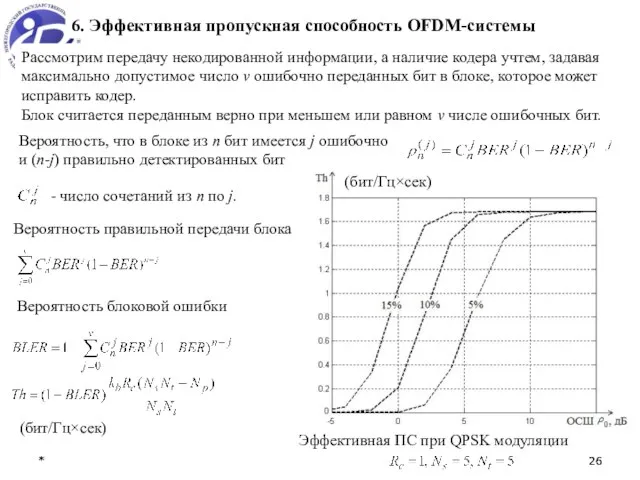
6. Эффективная пропускная способность OFDM-системы
Вероятность, что в блоке из n бит имеется j ошибочно и (n-j) правильно детектированных бит
- число сочетаний из n по j.
(бит/Гц×сек)
Эффективная ПС при QPSK модуляции
Рассмотрим передачу некодированной информации, а наличие кодера учтем, задавая максимально допустимое число v ошибочно переданных бит в блоке, которое может исправить кодер.
Блок считается переданным верно при меньшем или равном v числе ошибочных бит.
(бит/Гц×сек)
Вероятность блоковой ошибки
Вероятность правильной передачи блока

7. Некоторые сведения о преобразованиях Фурье
7.1. Дискретное преобразования Фурье (ДПФ)
- прямое ДПФ
Докажем, что обратное ДПФ
Доказательство:

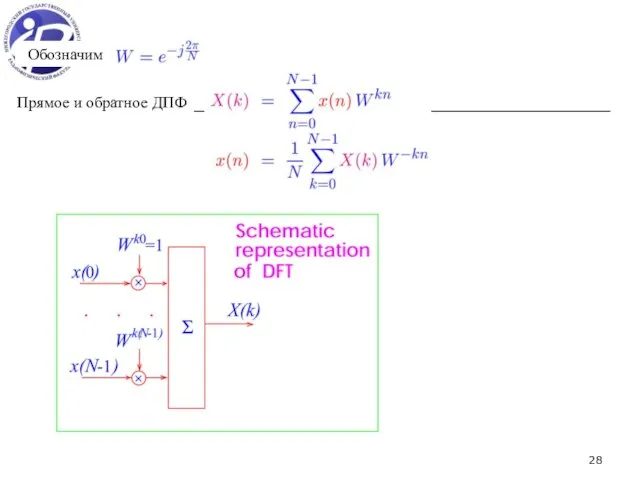
Обозначим
Прямое и обратное ДПФ

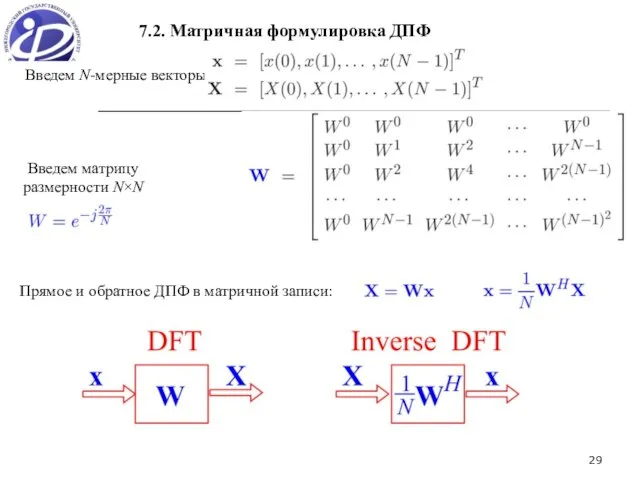
7.2. Матричная формулировка ДПФ
Введем N-мерные векторы
Введем матрицу размерности N×N
Прямое и обратное ДПФ в матричной записи:

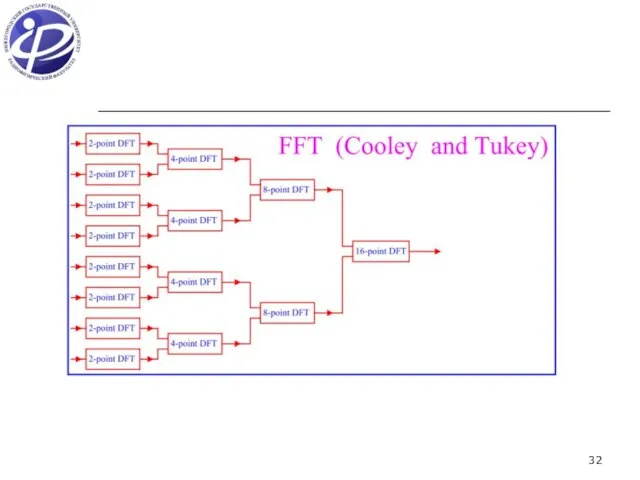
7.3. Быстрое преобразование Фурье (БПФ)
Введем новые обозначения:
Выше мы использовали обозначения X(k) и W без нижнего индекса N, показывающего длину последовательности.
Предположим, что длина преобразуемой последовательности – целая степень 2
Идея БПФ:

Или в краткой форме:
CN/2(k) и HN/2(k) – ДПФ размерности N/2, включающие четные и нечетные n, соответственно
1. N-точечное ДПФ с четным N может быть вычислено через два N/2- точечных ДПФ.
2. Если N/2 четное, то каждое из этих N/2- точечных ДПФ может быть вычислено через два N/4- точечных ДПФ и так далее.
3. Так как N=2r, то N, N/2, N/4 …. четные числа и процесс закончится 2-точечным ДПФ.

1. БПФ
7.4. Вычислительная сложность дискретных преобразований Фурье
2. ДПФ
Каждая стадия имеет N комплексных умножений и N комплексных сложений.
Всего имеется log2N стадий.
Полный объем вычислений
Полный объем вычислений
3. Сравнение
Использование БПФ дает выигрыш в
4. Пример.
N=210 = 1024.
CDFT = 220 ≈ 106. CFFT =10⋅1024 ≈ 104
Использование БПФ дает выигрыш в ≈100 раз.

*
Лекции 3-4. Преобразование аналоговой информации в цифровую форму
1. Дискретизация аналогового сигнала
- спектр сигнала x(t), где ω - круговая частота; δ(x) - дельта-функция
Периодический сигнал с периодом T имеет линейчатый спектр
Сигнал представляется рядом Фурье
Докажем, что
периодическая последовательность δ-импульсов имеет линейчатый спектр в виде периодической последовательности δ-компонент

*
Последовательность импульсов
Коэффициенты ряда Фурье
имеет период
Спектр
Доказали
Операция дискретизации.
- дискретный (семплированный) сигнал
Так как
то

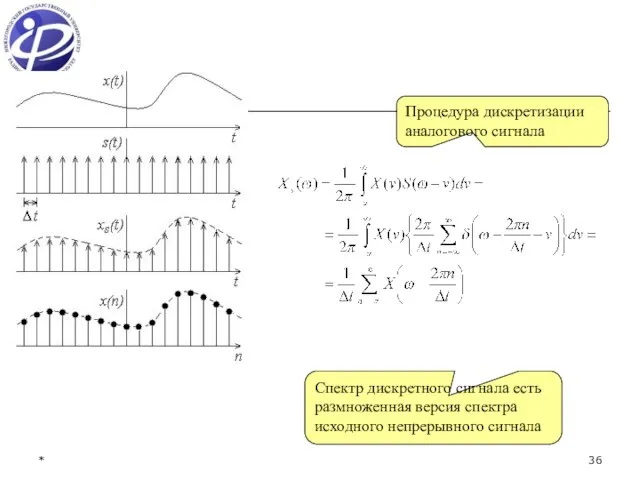
Процедура дискретизации аналогового сигнала
Спектр дискретного сигнала есть размноженная версия спектра исходного непрерывного сигнала
*

*
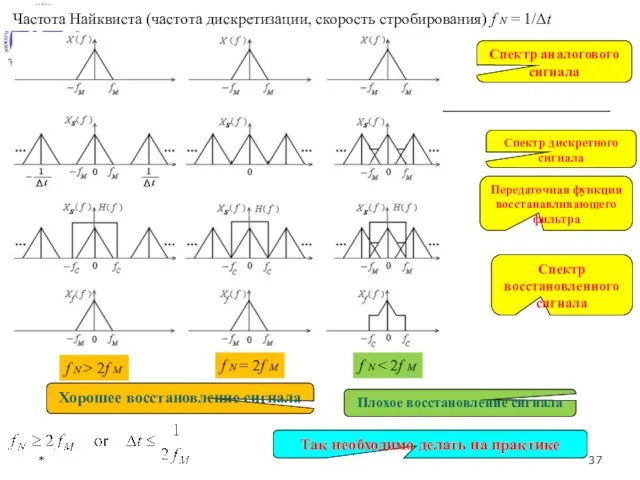
Хорошее восстановление сигнала
Так необходимо делать на практике
Частота Найквиста (частота дискретизации, скорость стробирования) f N = 1/Δt
Плохое восстановление сигнала
Спектр аналогового сигнала
Спектр дискретного сигнала
Передаточная функция восстанавливающего фильтра
Спектр восстановленного сигнала
f N > 2f M
f N = 2f M
f N < 2f M

*
2. Теорема Котельникова
Непрерывный сигнал с ограниченной полосой [−fM÷fM] может быть восстановлен по его отсчетам (выборкам), взятым через интервал времени Δt≤1/(2fM) с помощью интерполяционной формулы
Δtmax=1/(2fM) - максимальный интервал между временными отсчетами сигнала, определяемый шириной полосы
Доказательство. Сигнал можно восстановить в частотной области, используя идеальный низкочастотный фильтр
Идеальная передающая функция
(см. рисунок на слайде выше)
Идеальная импульсная характеристика

*
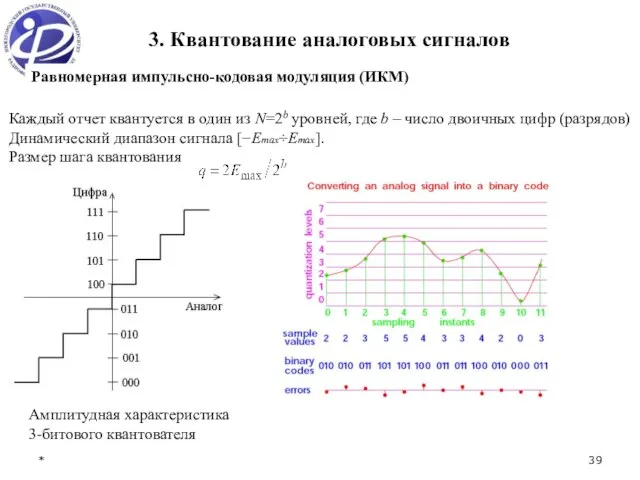
3. Квантование аналоговых сигналов
Равномерная импульсно-кодовая модуляция (ИКМ)
Каждый отчет квантуется в один из N=2b уровней, где b – число двоичных цифр (разрядов)
Динамический диапазон сигнала [−Emax÷Emax].
Размер шага квантования
Амплитудная характеристика 3-битового квантователя

*
Процесс квантования
где e – ошибка квантования, трактуемая как аддитивный шум с равномерной плотностью вероятности
Мощность
ошибки квантования
Мощность входного сигнала x при равномерной плотности вероятности на интервале от -Emax до +Emax
ОСШ увеличивается на 6 дБ на каждый разряд АЦП
Пример: 8-разрядный (b=8) АЦП (256 уровней). ОСШ = 48 дБ.

*
При неравномерной плотности вероятности сигнала на интервале от -Emax до +Emax
Пример. Сигнал x занимает часть динамического диапазона квантователя и имеет равномерную плотность вероятности на интервале (a >1)
Мощности сигнала
Пример: a=4. Тогда C=12 дБ.

*
Неравномерная импульсно-кодовая модуляция
В природе более вероятны более слабые сигналы.
Входной сигнал преобразуется в нелинейном устройстве (компрессор или сжиматель) и затем квантуется с помощью равномерной ИКМ.
При восстановлении сигнала используется обратное преобразование, выполняемое с помощью экспандера (расширителя)
Характеристика компрессора y=C(x). Размер шага квантования
Дисперсия ошибки квантования (плотность вероятности p(x) и характеристика компрессора y=C(x) произвольные)
Дисперсия сигнала
.
Устройство неравномерного квантования

*
ОСШ не должно зависеть от функции p(x)
x>0.
Компрессор должен быть логарифмическим
Граничные условия
x<0.

*
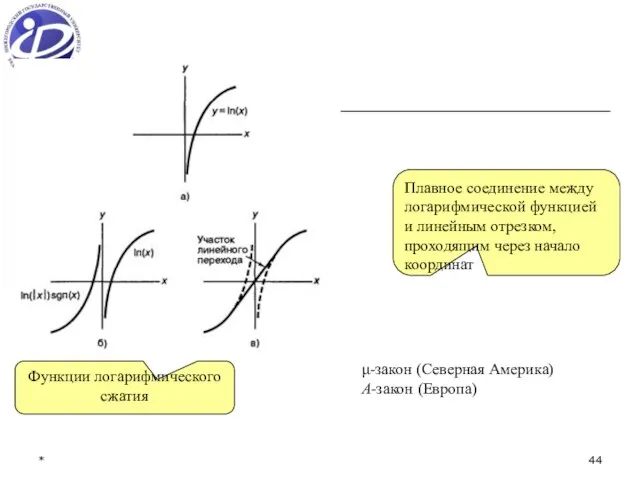
μ-закон (Северная Америка)
A-закон (Европа)
Плавное соединение между логарифмической функцией и линейным отрезком, проходящим через начало координат
Функции логарифмического сжатия

*
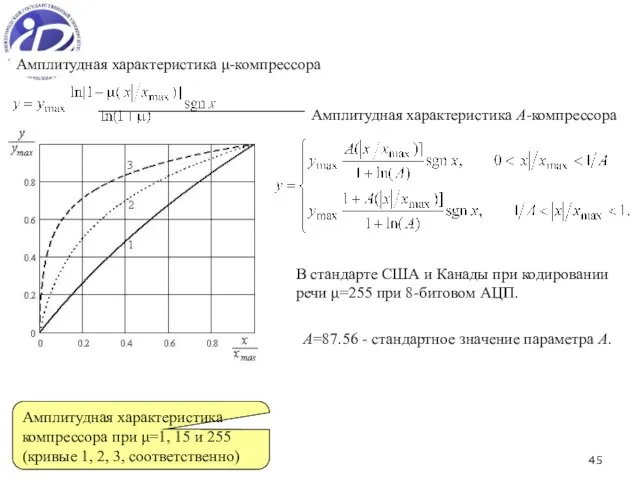
Амплитудная характеристика компрессора при μ=1, 15 и 255 (кривые 1, 2, 3, соответственно)
Амплитудная характеристика μ-компрессора
Амплитудная характеристика A-компрессора
A=87.56 - стандартное значение параметра A.
В стандарте США и Канады при кодировании речи μ=255 при 8-битовом АЦП.

*
Среднее ОСШ для μ-компрессора
μ=255 C=10.1 дБ.
ОСШ уменьшилось на 10.1 дБ. Однако теперь ОСШ не зависит от плотности вероятности входного сигнала

*
4. Кодирование дискретных источников
Кодовые слова переменной длины (при не равновероятных символах источника)
Должны выполняться два условия:
- требуется минимальное количество кодовых символов (бит) для передачи сообщения;
отсутствуют потери передаваемой информации (однозначное декодирование)
Для выполнения второго условия используются префиксные (мгновенные) коды, в которых начало более длинного кодового слова не совпадает с более коротким кодом.
В этом случае исключается неоднозначность при декодировании.
X множество всевозможных дискретных сообщений x1, x2, …, xn передается по каналу связи с вероятностями p(x1), p(x2), …, p(xn).
Условие непрерывной передачи: p(x1)+p(x2)+ … +p(xn)=1.
Энтропия источника (среднее количество информации при передаче одного символа сообщения)
- при равновероятных символах (p(xi)=1/n),
Кодовые слова фиксированной длины (при равновероятных символах источника)
Каждому из n символов источника ставится в соответствие R бит.
Эффективность кодирования – H/R (H – энтропия)
- n равно целой степени основания 2: число бит на символ источника R=log2(n), H/R=1
n не равно целой степени основания 2: число бит на символ R=⎣log2(n)⎦ +1, H/R<1

*
Пример. Четыре символа источника имеют вероятности (см. табл.) и кодируются, как показано в табл.
Код I (слева) не обеспечивает однозначное декодирование.
Код II (справа) обеспечивает однозначное декодирование
Принятая последовательность 001001 имеет два варианта декодирования (при коде I): a2a4a3 или а2а1а2а1

*
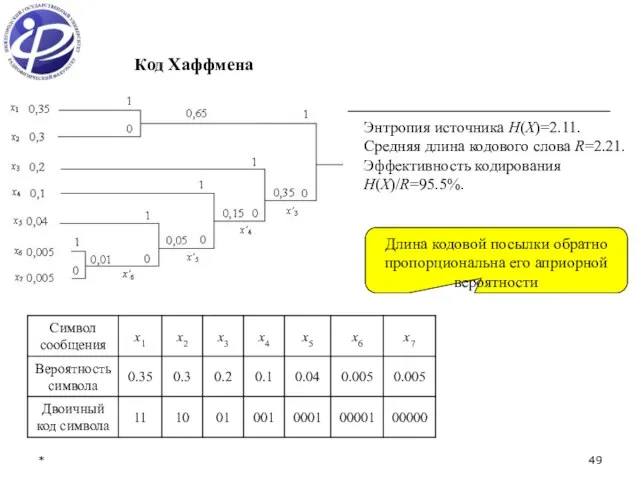
Энтропия источника H(X)=2.11. Средняя длина кодового слова R=2.21.
Эффективность кодирования H(X)/R=95.5%.
Код Хаффмена
Длина кодовой посылки обратно пропорциональна его априорной вероятности