Твердые тела

План
Основы физики твердого тела
кристаллы, векторы обратной решетки, брэгговская дифракция
динамика решетки, фононы, дисперсионные соотношения
зонная теория, модель Кронига-Пенни
Модель Дебая для теплоемкости
Теплопроводность
Л.Д. Ландау и Е.М. Лифшиц, Статистическая физика. Часть 1. (Том 5). – М.: Наука, 1976.
Дж. Блейкмор, Физика твердого тела. – М.: Мир, 1988.

Твердое тело в тепловом равновесии
Твердое тело – объект, атомы в котором совершают малые колебания относительно
узлов решетки для кристаллов
хаотически расположенных точек для аморфных тел
Потенциальная энергия взаимодействия минимальна при абсолютном нуле, поэтому колебания будут малыми и большинство тел становятся твердыми (кристаллизуются) при низких температурах. Исключением является жидкий гелий, для которого квантовые эффекты обеспечивают жидкое состояние при абсолютном нуле

Ближний и дальний порядок
Кристаллы обладают дальним порядком связей между соседями, то есть зная расположение атомов в одной области пространства, мы можем восстановить расположение атомов на большом расстоянии. В качестве меры корреляции положений атомов в различных точках твердого тела выбирают двухточечную функцию Паттерсона (ρ – отклонение плотности от среднего значения)

Ближний и дальний порядок
Кристаллы обладают дальним порядком связей между соседями, то есть зная расположение атомов в одной области пространства, мы можем восстановить расположение атомов на большом расстоянии
Аморфные тела проявляют ближний порядок в связях между ближайшими соседями, хотя степень их упорядоченности зависит от условий приготовления. Примерами аморфных тел
являются статистические
полимеры, угольная сажа,
селен и сурьма, стекла и
аморфный кремний

Ближний и дальний порядок
Кристаллы обладают дальним порядком связей между соседями
Аморфные тела проявляют ближний порядок в связях между ближайшими соседями
Непериодические квазикристаллы обладают определенной симметрией и характеризуются дальним порядком
Примером на плоскости
является мозаика Пенроуза,
имеющая осевую симметрию
5-го порядка, что запрещено
классической кристаллографией
Нобелевская премия по химии 2011 (Д. Шехтман)

Остаточная энтропия при абсолютном нуле
Аморфные тела метастабильны, но с очень большим временем релаксации, так что они ведут себя как устойчивые твердые тела. Однако в силу того, что эта система неравновесная, теорема Нернста неприменима и при абсолютном нуле энтропия не равна нулю, что не сказывается на теплоемкости
Остаточная энтропия наблюдается также в не вполне упорядоченных кристаллах, когда при низкой температуре атомы могут «вмораживаться» на чужие места, тогда число узлов превышает число атомов и вероятность находиться там будет отлична от 1. Например, для молекулы CO возможны С-О и О-С, т.е. получается число возможных состояний вдвое больше, и остаточная энтропия будет ln2

Степени свободы твердого тела
Степени свободы 3Nn (N –число ячеек, n – число атомов в ячейке)
3 поступательные
3 вращательные
3Nn-6 колебательных (приблизительно 3Nn)
В термодинамике нас будут интересовать колебания атомов в решетке, считая внутренние (электронные) степени свободы атомов несущественными (в металлах они играют важную роль!)
Колебательные степени свободы есть совокупность 3Nn осцилляторов, причем квантованные колебания решетки называются фононами

Упругие волны в кристаллах
Волна колебаний периодической решетки – систематическая последовательность смещений атомов из положения равновесия (продольных и поперечных)
Скорость продольных волн можно выразить через модуль объемной упругости B (коэффициент жесткости) и плотность ρ
В общем случае применяется тензор жесткости, т.е. скорость звука зависит от направления распространения звуковой волны, как и скорость волны в оптике анизотропных сред
Скорости поперечных волн

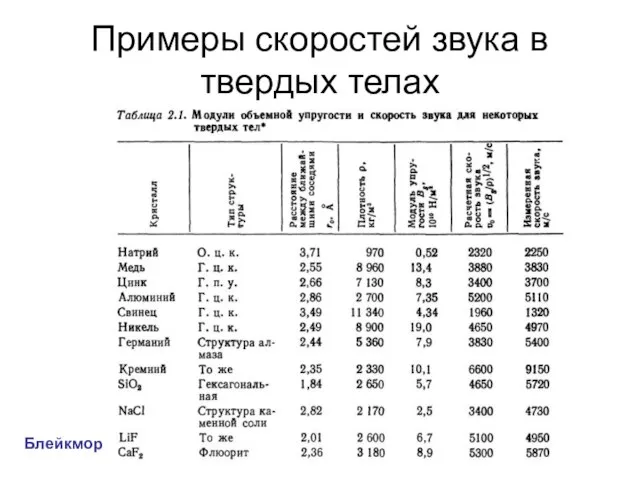
Примеры скоростей звука в твердых телах
Блейкмор

Динамика атомной решетки
Формулой можно пользоваться только в том
случае, если твердое тело считать сплошной средой, игнорируя атомную структуру (макроскопический подход, применимый при длине упругой волны, намного превышающей межатомное расстояние)
В общем случае нужно рассматривать движение упругой волны, приводящее к смещениям атомов из положений равновесия.
При этом важным для
вычислений оказывается
периодичность расположения
атомов

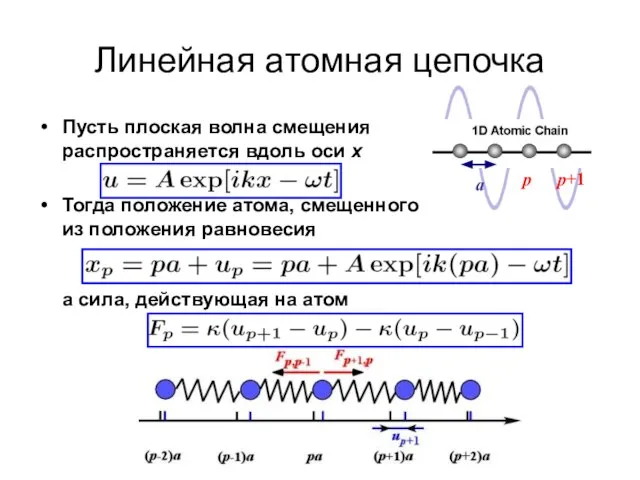
Линейная атомная цепочка
Пусть плоская волна смещения
распространяется вдоль оси х
Тогда положение атома, смещенного
из положения равновесия
а сила, действующая на атом
a
p
p+1

Дисперсия цепочки
Исходя из 2-го закона динамики Ньютона
приходим к уравнению для смещения
Подстановка решения
приводит к дисперсионному соотношению

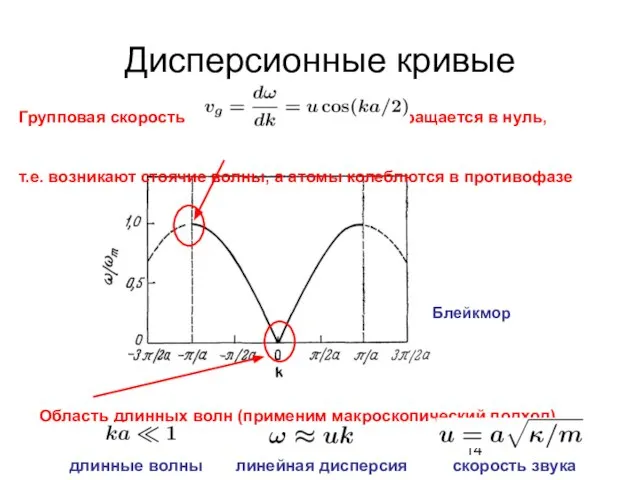
Дисперсионные кривые
Область длинных волн (применим макроскопический подход)
длинные волны
линейная дисперсия
скорость звука
Групповая скорость обращается в нуль,
т.е. возникают стоячие волны, а атомы колеблются в противофазе
Блейкмор

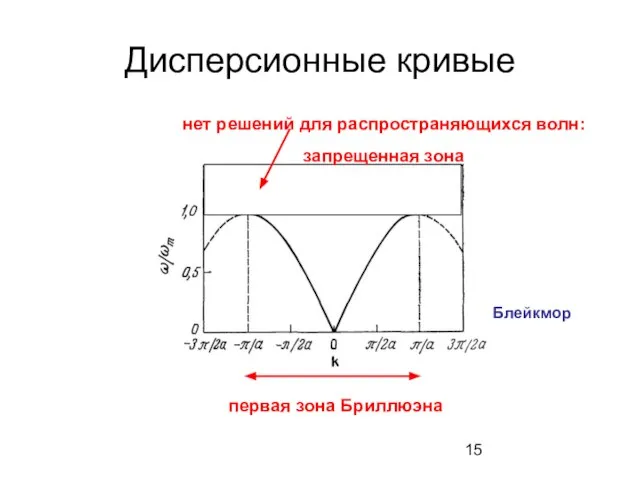
Дисперсионные кривые
первая зона Бриллюэна
нет решений для распространяющихся волн:
запрещенная зона
Блейкмор

Векторы обратной решетки
Волновые векторы принадлежат не реальному пространству векторов, а обратному пространству
Трансляции в обратном пространстве описываются векторами обратной решетки
также, как трансляции в реальной решетке
Базисные векторы обратной решетки равны

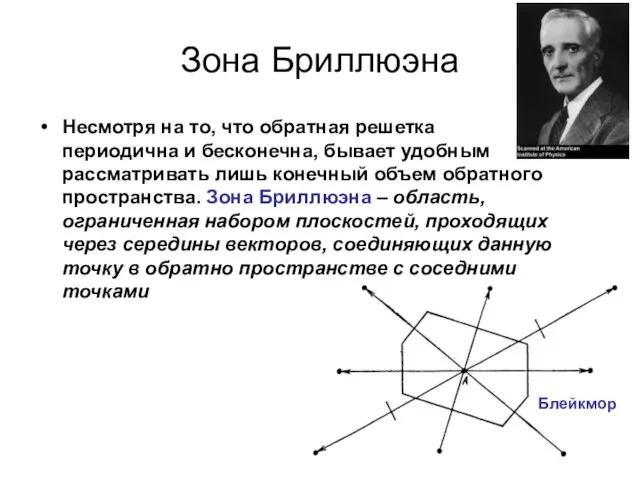
Зона Бриллюэна
Несмотря на то, что обратная решетка
периодична и бесконечна, бывает удобным рассматривать лишь конечный объем обратного пространства. Зона Бриллюэна – область, ограниченная набором плоскостей, проходящих через середины векторов, соединяющих данную точку в обратно пространстве с соседними точками
Блейкмор

Дифракция Брэгга (1912)
(h,k,l) задают плоскости в реальном
пространстве. Падающая волна отражается от одной из таких плоскостей, причем в обратном пространстве выполняется закон сохранения «импульса», который при условии Брэгга (интерференции с усилением) сводится к
и из которого следует
Блейкмор

Дифракция Брэгга
Условие брэгговской дифракции можно переписать для компонент изменения волнового вектора в реальном пространстве
Уравнения Лауэ (1912)
Построение Эвальда (1921): условие
Брэгга удовлетворяется всякий раз,
когда сфера проходит через узел
обратной решетки кристалла
Блейкмор

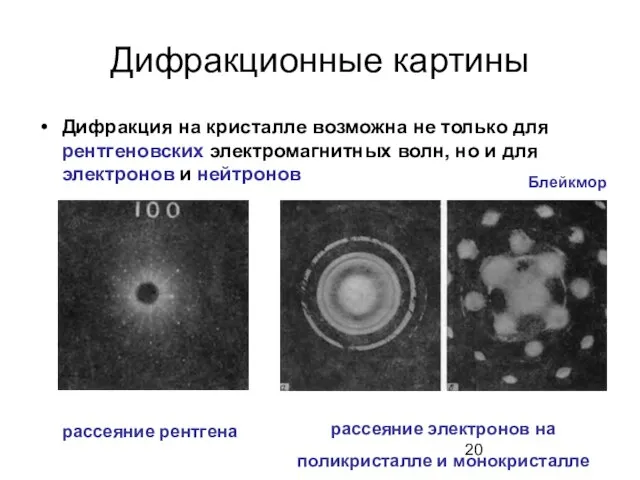
Дифракционные картины
Дифракция на кристалле возможна не только для рентгеновских электромагнитных волн, но и для электронов и нейтронов
рассеяние рентгена
рассеяние электронов на
поликристалле и монокристалле
Блейкмор

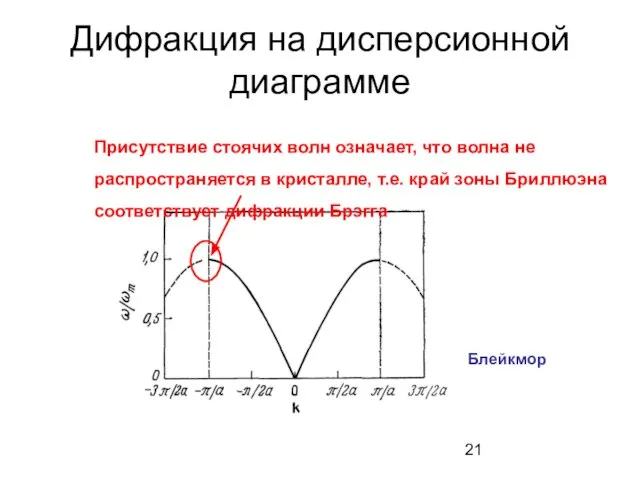
Дифракция на дисперсионной диаграмме
Присутствие стоячих волн означает, что волна не
распространяется в кристалле, т.е. край зоны Бриллюэна
соответствует дифракции Брэгга
Блейкмор

Двухатомная линейная
цепочка атомов
Пусть теперь есть атомы разных сортов, с массами m и M>m и возбуждается продольное возмущение. Мы полагаем, что волна имеет одни и те же волновое число и частоту, но амплитуды колебаний различные
Уравнения движения
B

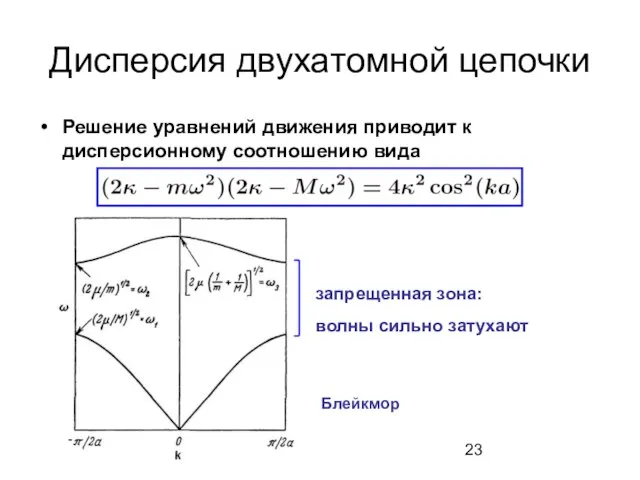
Дисперсия двухатомной цепочки
Решение уравнений движения приводит к дисперсионному соотношению вида
запрещенная зона:
волны сильно затухают
Блейкмор

Акустическая и оптическая
ветви спектра
акустическая ветвь
оптическая ветвь:
колебания можно возбудить
светом (в кристаллах с ионной
связью), атомы разных масс
движутся в противофазе
Блейкмор

Колебания 3D кристаллической решетки
Пусть положение элементарной ячейки задается радиусом-вектором
или вектором
Тогда функция Лагранжа для атомов со смещениями us (s=1,…,n – номер атома в ячейке)
Уравнение движения решетки

Дисперсионное уравнение
Записывая решение в виде плоской волны
приходим к системе 3n линейных уравнений
где
Тогда дисперсионное уравнение
имеет следующие решения , где
амплитуда и поляризация волны

Свойства дисперсионных кривых
3n дисперсионных кривых
четные функции
в силу зависимости волновые векторы определены с точностью до вектора обратной решетки
Поэтому можно ограничиться конечной полосой волновых векторов, лежащих в первой зоне Бриллюэна
некоторые частоты могут совпадать при определенной симметрии – вырождение

Оптические и акустические ветви
Среди 3n ветвей
3 акустические ветви (при малых k решетка колеблется, как сплошная среда, и частота обращается в нуль при k=0). Закон дисперсии может быть выражен однородной функцией первого порядка
3n-3 оптические ветви (при k=0 частота отлична от нуля и называется предельной). В силу четности зависимости частоты от волнового вектора вблизи нуля можно сделать разложение в ряд

Трехмерный кристалл
Для n атомов в ячейке и N ячеек возникает
N продольных акустических колебаний
2N поперечных акустических колебаний
(n-1)N продольных оптических колебаний
2(n-1)N поперечных оптических колебаний
Дисперсионные кривые:
3 акустические кривые
3n-3 оптические кривые
Дисперсионные кривые кристалла алмаза
Блейкмор

Смещение атома с учетом
всех волн спектра
Решение представляет собой лишь одну волну. На самом деле, необходимо писать суперпозицию всех волн
Это выражение можно переписать как
Здесь амплитуда
а поляризация нормирована согласно

Энергия колебаний решетки
Смещение
записано для бесконечного кристалла. Для кристалла, состоящего из N ячеек, интегрирование по обратному пространству нужно заменить на суммирование по конечному числу колебаний
При этом энергия колебательных степеней свободы
или

Квантование колебаний
После введения канонических переменных
гамильтониан классической системы осцилляторов (решетки) примет вид суммы независимых нормальных колебаний
Квантование заключается в замене канонических переменных на операторы координат и импульсов
удовлетворяющих коммутационному правилу

Операторы рождения и уничтожения фононов
Энергия системы квантовых осцилляторов – квазичастиц фононов, элементарных возбуждений – равна
По обычной схеме можно ввести операторы рождения и уничтожения
Оператор смещений атомов примет вид

Фононы
Вместо смещений атомов в квантовой теории говорят о распространяющихся по решетке квазичастицах – фононах. Для них выполняются те же соотношения, что и для фотонов
однако p в данном случае – квазиимпульс, определенный с точностью до постоянного вектора обратной решетки
Свойства спектра классических колебаний переносятся на спектр фононов ε(p)
Для гармонических колебаний в бесконечном идеальном кристалле взаимодействие фононов и установление теплового равновесия невозможно! Ангармоническое возмущение (рассеяние фононов) описывается теперь оператором смещения (т.е. операторами рождения и уничтожения фононов)

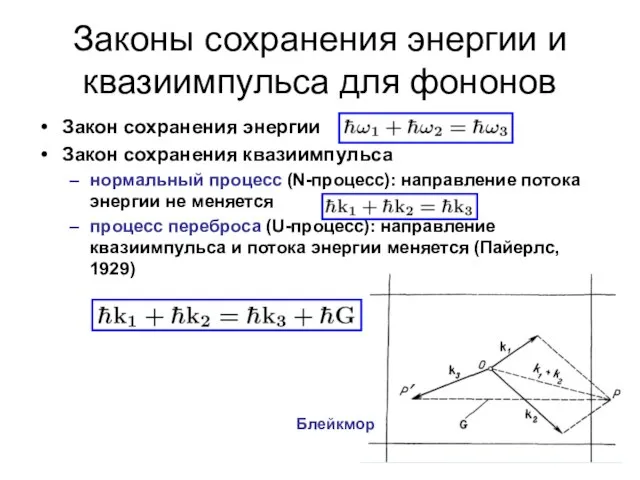
Законы сохранения энергии и квазиимпульса для фононов
Закон сохранения энергии
Закон сохранения квазиимпульса
нормальный процесс (N-процесс): направление потока энергии не меняется
процесс переброса (U-процесс): направление квазиимпульса и потока энергии меняется (Пайерлс, 1929)
Блейкмор

Зонная теория твердых тел
Кроме колебаний решетки в твердом теле возможно также движение электронов. Ранее мы уже рассматривали свободные электроны. Такая модель хорошо работает, если не нужно рассматривать процессы рассеяния электронов на дефектах, на фононах, на электронах
Зонная теория твердых тел нужна для объяснения
длины свободного пробега,
электро- и теплопроводности,
существования металлов и изоляторов

Положения зонной теории
Согласно зонной теории
периодическая потенциальная энергия для электрона в кристалле
волновая функция состояния вводится для идеальной периодической решетки, а рассеяние трактуется, как возмущение
теория строится для одного электрона, причем действие всего остального кристалла описывается с помощью эффективной потенциальной энергии V(r)
решается одноэлектронное уравнение Шредингера
причем заполнение состояний происходит в согласии со статистикой Ферми-Дирака

Функции Блоха
Ф. Блох (1928) предположил, что потенциал V(r) состоит из
периодического потенциала атомов без колебаний (фононов)
потенциала всех внешних электронов. Предполагается, что он тоже периодический и таким образом грубо учитывает электрон-электронное взаимодействие
Для одномерной решетки с периодом a (потенциал ) наложим циклическое граничное условие типа Борна-Кармана, состоящее в том, что волновая функция повторяется через N атомов

Функции Блоха
Пусть при трансляции на одну ячейку волновая функция изменяется согласно
После N трансляций
Данное уравнение решается:
Задав волновое число согласно
приходим к функции Блоха
первая зона Бриллюэна

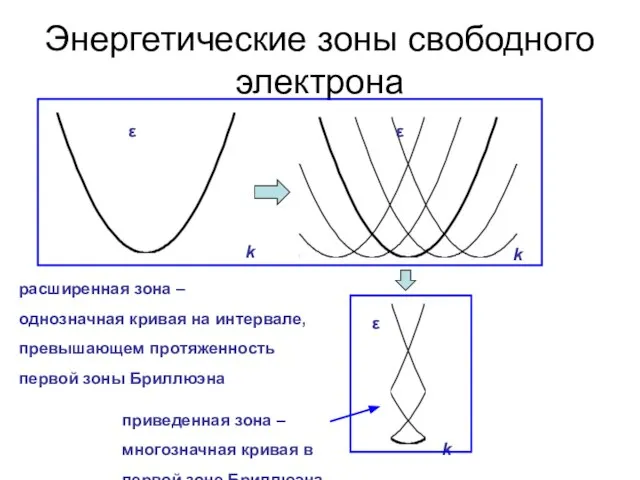
Энергетические зоны свободного электрона
ε
k
ε
ε
k
k
приведенная зона –
многозначная кривая в
первой зоне Бриллюэна
расширенная зона –
однозначная кривая на интервале,
превышающем протяженность
первой зоны Бриллюэна

Модель Кронига-Пенни
В одномерной модели
Кронига и Пенни
используются
прямоугольные
потенциальные барьеры
Для электроны
свободные
Если же барьеры очень широкие, так что туннелирование маловероятно, то энергия квантуется, как в потенциальной яме
Блейкмор

Модель Кронига-Пенни
Рассмотрим очень высокие, но очень узкие барьеры, когда остается конечным, т.е. потенциалы можно представить дельта-функциями
Решение уравнения в области 0

Дисперсионное уравнение
Благодаря теореме Блоха
функции в области a функции в 0
Граничные условия
приводят к дисперсионному уравнению

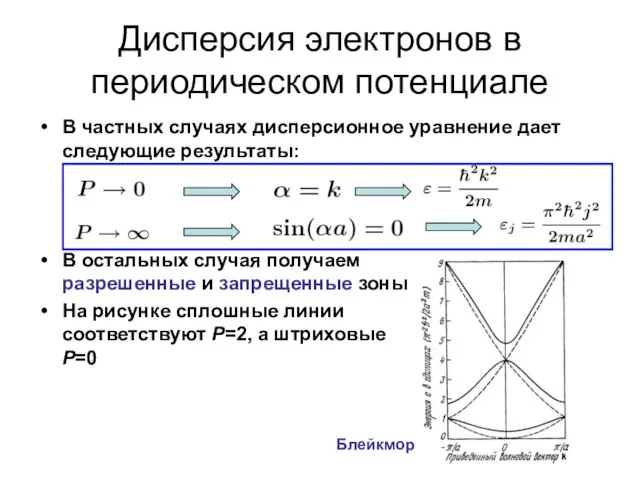
Дисперсия электронов в периодическом потенциале
В частных случаях дисперсионное уравнение дает следующие результаты:
В остальных случая получаем
разрешенные и запрещенные зоны
На рисунке сплошные линии
соответствуют P=2, а штриховые
P=0
Блейкмор

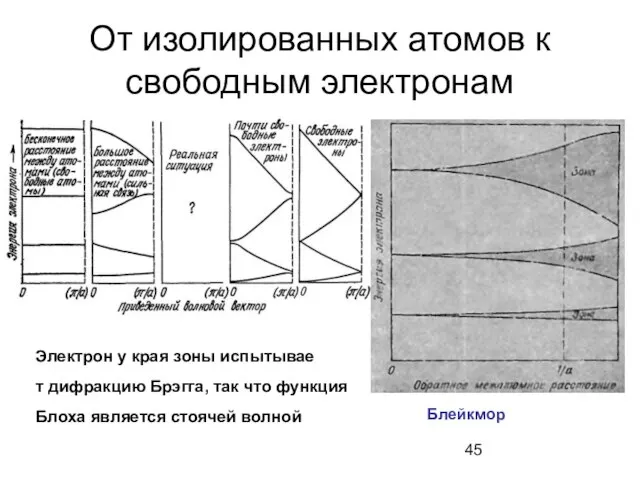
От изолированных атомов к свободным электронам
Электрон у края зоны испытывае
т дифракцию Брэгга, так что функция
Блоха является стоячей волной
Блейкмор

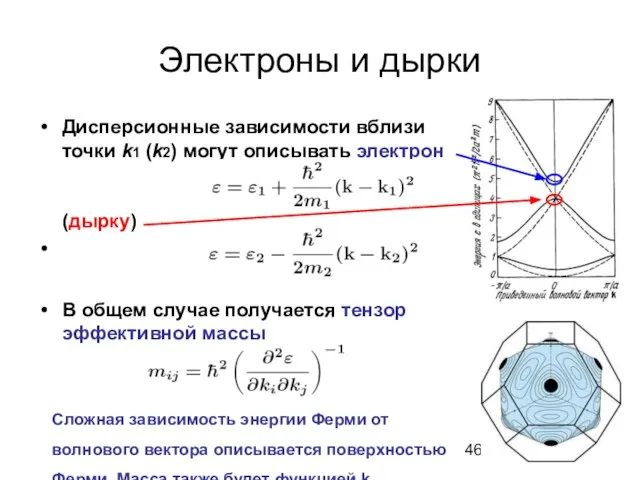
Электроны и дырки
Дисперсионные зависимости вблизи
точки k1 (k2) могут описывать электрон
(дырку)
В общем случае получается тензор
эффективной массы
Сложная зависимость энергии Ферми от
волнового вектора описывается поверхностью
Ферми. Масса также будет функцией k

Число колебаний решетки
Число состояний в случае
колебаний решетки приводится к виду
Мы ввели локальную систему координат в k-пространстве, две оси лежат на изочастотной поверхности, а третья ось – перпендикулярно ей. Зависимости от волновых векторов на изочастотной поверхности, очевидно, не будет. Частота может меняться при выходе за пределы поверхности, т.е.
Следовательно,

Плотность числа
колебаний решетки
Число колебаний решетки
Плотность числа колебаний
Например, при законе дисперсии
плотность числа колебаний похожа на плотность состояний свободной частицы в трехмерном пространстве
Аналогичные соотношения выполняются и для электронов

Теплоемкость
Кроме теплоемкости электронов, которую мы оценили ранее для вырожденного электронного газа, нужно рассчитать также теплоемкость колебаний решетки (газа фононов)
Исторически было несколько моделей теплоемкости твердого тела
классическая модель (закон Дюлонга-Пти): при больших температурах теплоемкость равна (3Nn)kBT
модель Эйнштейна: все атомы в кристалле колеблются с одинаковой частотой, т.е. g(ω)=3Nnδ(ω- ω0)
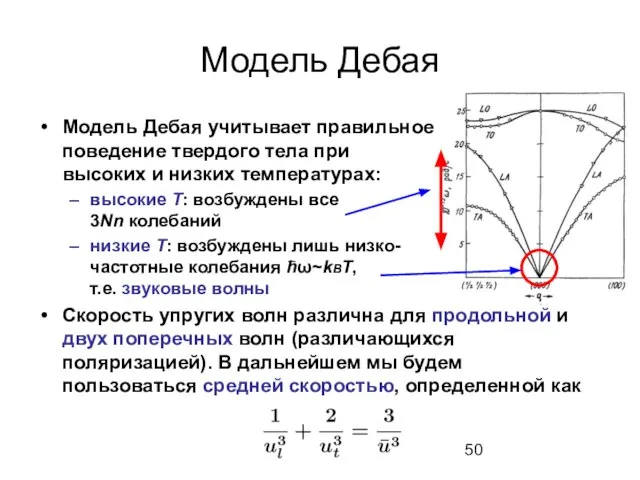
модель Дебая: колебания распределены по частотам с помощью плотности состояний g(ω)

Модель Дебая
Модель Дебая учитывает правильное
поведение твердого тела при
высоких и низких температурах:
высокие Т: возбуждены все
3Nn колебаний
низкие Т: возбуждены лишь низко-
частотные колебания ћω~kBT,
т.е. звуковые волны
Скорость упругих волн различна для продольной и двух поперечных волн (различающихся поляризацией). В дальнейшем мы будем пользоваться средней скоростью, определенной как

Плотность состояний
в модели Дебая
Полагая линейный закон дисперсии ω=uk для продольных и поперечных звуковых волн, из общей формулы
выводим
Предположение о линейности закона дисперсии выполняется лишь при низких температурах. В общем случае мы получаем лишь интерполяционную, приближенную формулу, для которой требуем, чтобы полное число колебаний было равно 3Nn
предельная частота

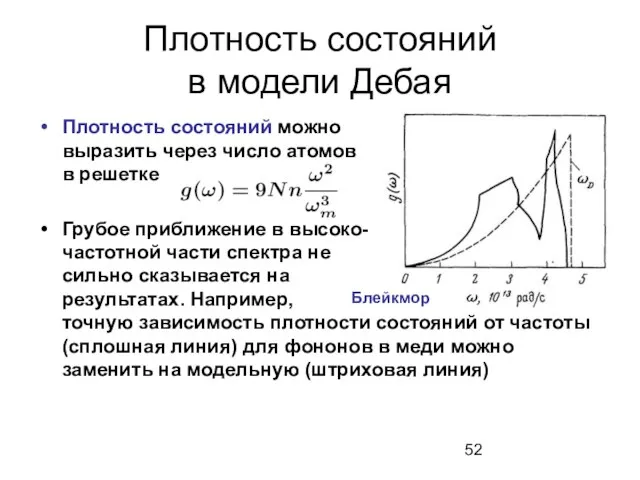
Плотность состояний
в модели Дебая
Плотность состояний можно
выразить через число атомов
в решетке
Грубое приближение в высоко-
частотной части спектра не
сильно сказывается на
результатах. Например,
точную зависимость плотности состояний от частоты (сплошная линия) для фононов в меди можно заменить на модельную (штриховая линия)
Блейкмор

Температура Дебая
В свободной энергии системы квантовых осцилляторов
заменяем сумму на интеграл по всем частотам от нуля до предельной частоты
Сделаем замену переменной интегрирования
и введем дебаевскую характеристическую температуру твердого тела
энергия атомов в положениях равновесия

Теплоемкость твердого тела
Интегрируя
по частям, мы приходим к
где введена функция Дебая
Тогда внутренняя энергия тела
а его теплоемкость

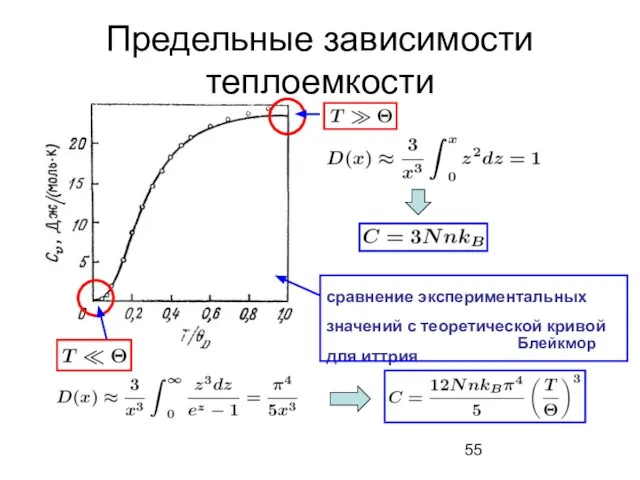
Предельные зависимости теплоемкости
сравнение экспериментальных
значений с теоретической кривой
для иттрия
Блейкмор

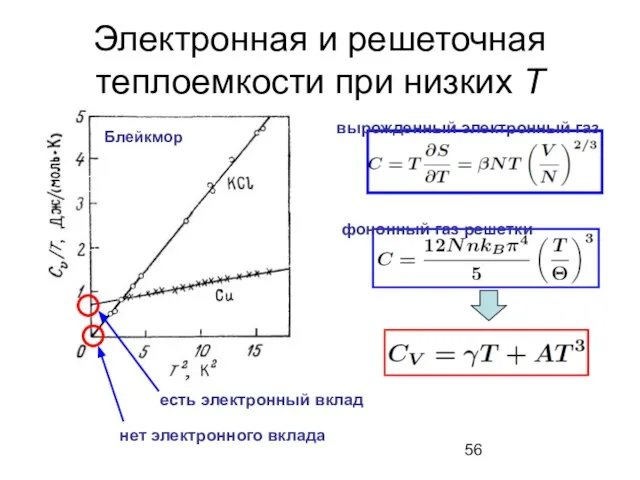
Электронная и решеточная теплоемкости при низких Т
вырожденный электронный газ
фононный газ решетки
есть электронный вклад
нет электронного вклада
Блейкмор

Тепловое расширение
твердых тел
Очевидно, свободную энергию
и потенциал Гиббса (согласно теореме о малых добавках) можно представить в виде
Тогда
Коэффициент теплового расширения

Тепловое расширение
твердых тел
Записывая теплоемкость
и вычисляя отношение
замечаем, что это отношение положительно, потому что и при сжатии тела будет уменьшаться амплитуда колебаний атомов, т.е. увеличиваться частота колебаний, значит
Отметим также, что независимость от температуры
отношения составляет суть закона Грюнейзена

Теплоемкости при постоянном давлении и объеме
До этого мы не различали теплоемкостей при постоянном объеме и давлении, считая их примерно одинаковыми. При малых температурах их разность много меньше теплоемкости согласно теореме Нернста. При больших температурах
а разность теплоемкостей, вычисленная согласно
будет пропорциональна температуре, т.е. представляет первый порядок малости по отношению ко всей теплоемкости

Применимость модели Дебая
В модели Дебая мы подразумевали, что твердое тело изотропно, поэтому закон дисперсии был ω=uk. В общем случае кристаллы анизотропны. Например, в «слоистых» кристаллах энергия взаимодействия атомов в слое много сильнее энергии взаимодействия между слоями (графит). В этом случае будет несколько температур Дебая, и закон Т3 выполняется лишь при температурах, меньших по сравнению с наименьшей дебаевской температурой.
3

Слоистый кристалл
Закон дисперсии звуковых волн
Свободная энергия при низких Т равна
где суммирование производится по трем акустическим ветвям спектра. Подставляя законы дисперсии, можно показать, что теплоемкость при увеличении температуры будет меняться от кубической до линейной зависимости от температуры

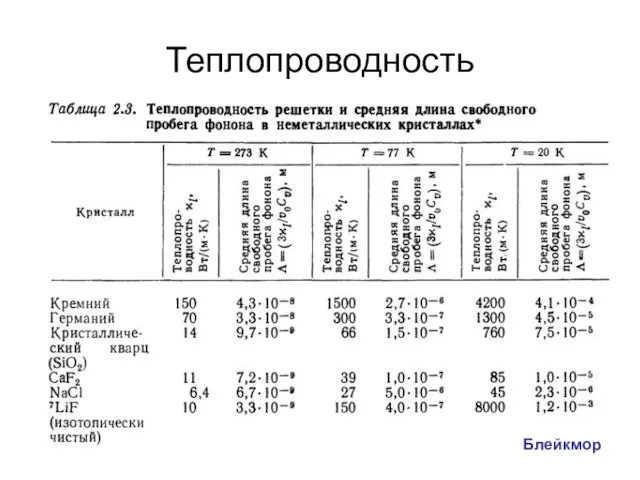
Теплопроводность
Тепловая энергия может передаваться
свободными электронами, дырками (этот вклад доминирует в металлах)
фононами (в не-металлах)
фотонами (при очень высоких температурах)
электронно-дырочными парами
связанными электронно-дырочными парами (экситонами)
Рассмотрим фононный механизм для описания теплопроводности. В тепловом равновесии скорости потоков фононов в противоположных направлениях равны и общий поток отсутствует.

Теплопроводность
Для неравновесного фононного газа скорость потока энергии через единичную площадку, перпендикулярную градиенту температуры
где теплопроводность при температурах много ниже температуры Дебая
Средняя длина свободного пробега фононов Λ
бесконечная при отсутствии фонон-фононного взаимодействия (ангармонизма) в идеальном кристалле
большая при малых энергиях фононов
малая для больших энергий фононов, когда становятся важны процессы переброса

Теплопроводность
Блейкмор

Рассеяние фононов
Рассеяние
фононов на фононах (ангармонизм + процессы переброса)
фононов на точечных дефектах (примесях и вакансиях)
фононов на линейных дефектах (дислокациях)
фононов на внешних поверхностях монокристаллов
фононов на случайном распределении различных изотопов химических элементов
Поэтому в кристаллах плохого качества Λ остается малой при всех температурах