Содержание
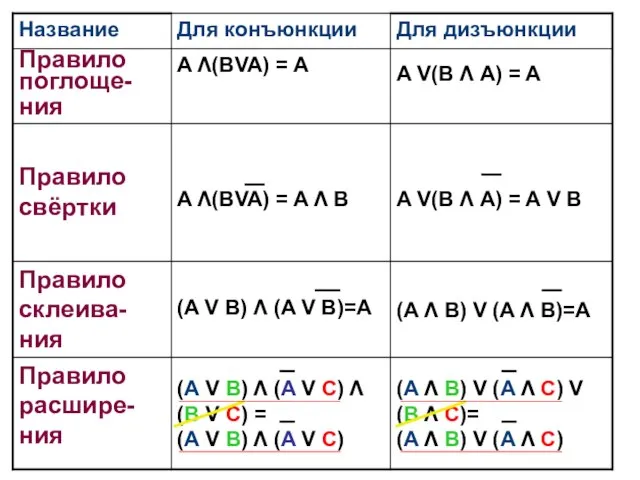
- 3. Минимизация логических выражений (функций) Упражнения 1. Найдите значения выражений: А) (1 V1) V (1V0) = 1
- 4. Решение примеров на минимизацию логических выражений и функций 1. (A + ¬B)(¬A + B) A B
- 5. Логическое следование(импликация) Логическое следование(импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».
- 6. ЕГЭ 2006 A9 Для какого из указанных значений числа X истинно высказывание: (X>4) \/ ((X>1) ⇒X>4))?
- 7. ЕГЭ 2007 A9 Для какого числа X истинно высказывание ((X>3) \/(X 1)1 2)2 3)3 4)4 A10
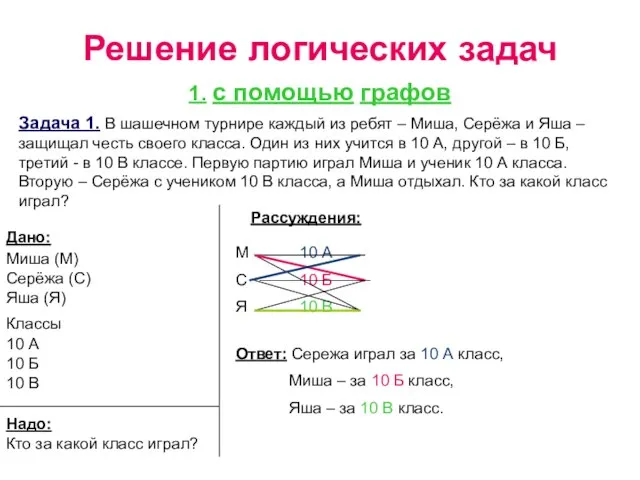
- 8. Решение логических задач 1. с помощью графов Задача 1. В шашечном турнире каждый из ребят –
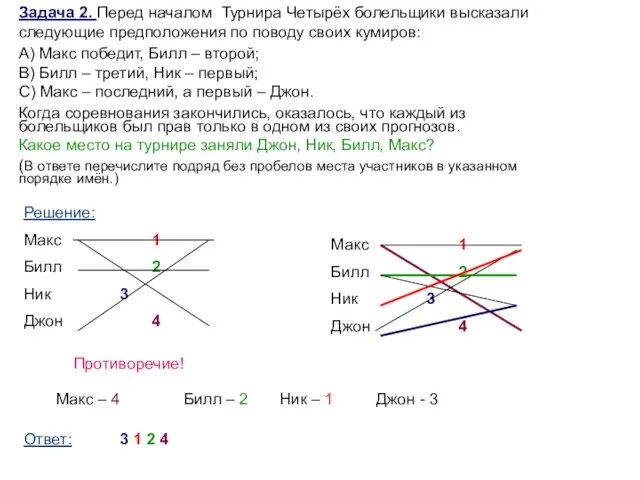
- 9. Задача 2. Перед началом Турнира Четырёх болельщики высказали следующие предположения по поводу своих кумиров: А) Макс
- 10. Задача 3. В начале лета школьники организовали сельскохозяйственную бригаду и избрали бригадира, заместителя бригадира и звеньевых
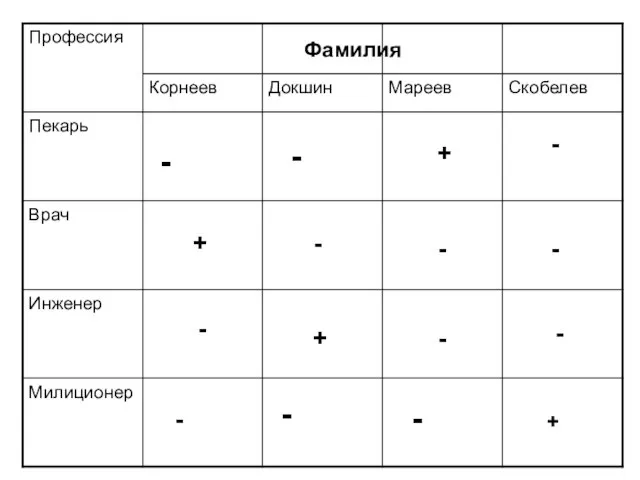
- 11. 2. с помощью таблиц Задача 4. Корнеев, Докшин, Мареев и Скобелев –жители нашего города. Их профессии
- 12. Фамилия - - - - - + + - + + -
- 14. Скачать презентацию







 Государственные символы России
Государственные символы России Геосинтетические продукты
Геосинтетические продукты Sights Of Russia
Sights Of Russia Виртуальная экскурсия по дому-музею П.П. Бажова в Сысерти
Виртуальная экскурсия по дому-музею П.П. Бажова в Сысерти Проектный метод в управлении
Проектный метод в управлении Enlightenment in America
Enlightenment in America Мужчины и женщины. Прирост населения
Мужчины и женщины. Прирост населения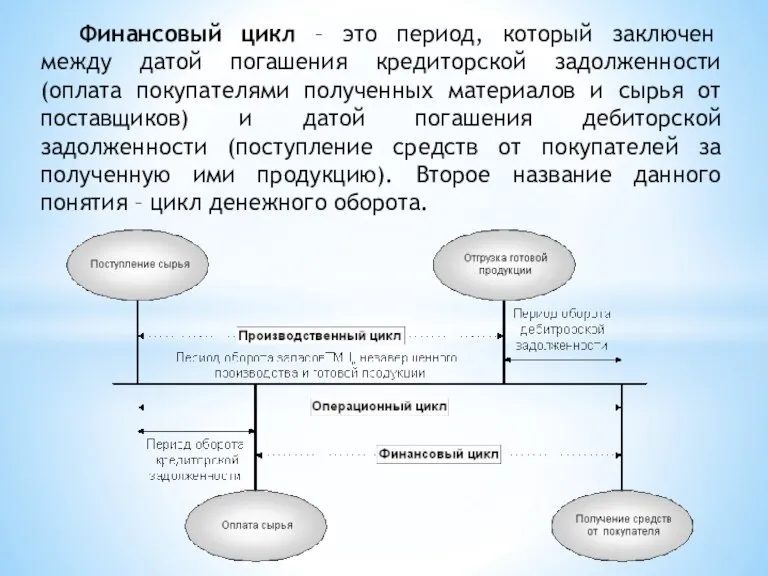 Цикл денежного оборота
Цикл денежного оборота Известные имена. Софья Ковалевская
Известные имена. Софья Ковалевская Сатирические образы человека
Сатирические образы человека Три ступени к успеху1. Причины личной неэффективности2. Как стать эффективным? Личная цель3. Персональная стратегия успеха
Три ступени к успеху1. Причины личной неэффективности2. Как стать эффективным? Личная цель3. Персональная стратегия успеха Как нам жить в дружбе с природой?
Как нам жить в дружбе с природой? Что в имени твоём
Что в имени твоём Маленький вклад в большую Победу
Маленький вклад в большую Победу Франчайзинг кофеенFRIENDS’TIME™
Франчайзинг кофеенFRIENDS’TIME™ Права ребенка
Права ребенка Здесь мой дом
Здесь мой дом Налогообложение предпринимательской деятельности
Налогообложение предпринимательской деятельности Презентация на тему Жизнь на разных материках (5 класс)
Презентация на тему Жизнь на разных материках (5 класс) Внешняя политика Александра I в 1801-1812 годах
Внешняя политика Александра I в 1801-1812 годах Презентация на тему Ценообразующие факторы продуктов питания
Презентация на тему Ценообразующие факторы продуктов питания  Вакуумный формовщик
Вакуумный формовщик Химический эксперимент в школе – элемент формирования исследовательской компетенции
Химический эксперимент в школе – элемент формирования исследовательской компетенции Русский романтический пейзаж
Русский романтический пейзаж Учет и анализ движения денежных средств
Учет и анализ движения денежных средств Команда
Команда Храмы (фотографии)
Храмы (фотографии) Роман в стихах А.С. Пушкина « Евгений Онегин»
Роман в стихах А.С. Пушкина « Евгений Онегин»