Содержание
- 2. История Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.),
- 3. Интеграл функции — аналог суммы последовательности. Неформально, (определённый) интеграл является площадью части графика функции (в пределах
- 4. Интеграл Определённый интеграл Неопределённый интеграл
- 5. Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая
- 6. Неопределённый интегра́л для функции f(x), — это совокупность всех первообразных данной функции. Если функция определена и
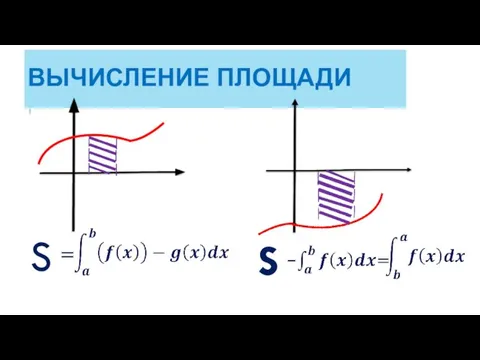
- 7. ВЫЧИСЛЕНИЕ ПЛОЩАДИ S S
- 8. Таблица интегралов
- 10. Скачать презентацию





 Заботливые родители здоровые и счастливые дети
Заботливые родители здоровые и счастливые дети Линейное уравнение с одним неизвестным
Линейное уравнение с одним неизвестным Issledovanie-funkciy-i-postroenie-grafikov.ppt
Issledovanie-funkciy-i-postroenie-grafikov.ppt Презентация на тему философия тождества
Презентация на тему философия тождества  Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Типы иррациональных уравнений Примеры решения
Типы иррациональных уравнений Примеры решения  Степень с отрицательным показателем
Степень с отрицательным показателем Что изучает алгебра - презентация по Алгебре_
Что изучает алгебра - презентация по Алгебре_ Квадратные уравнения и уравнения, приводимые к квадратным - презентация по Алгебре_
Квадратные уравнения и уравнения, приводимые к квадратным - презентация по Алгебре_ Презентация на тему Закон наиболее тесной связи (the law of the real connection)
Презентация на тему Закон наиболее тесной связи (the law of the real connection)  Процентные вычисления в жизненных ситуациях
Процентные вычисления в жизненных ситуациях Степенная функция - презентация по Алгебре_
Степенная функция - презентация по Алгебре_ Итоговое тестирование по алгебре 7 класс
Итоговое тестирование по алгебре 7 класс Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными  Применение производной
Применение производной Тема урока: Решение уравнений с параметром Урок формирования знаний и умений
Тема урока: Решение уравнений с параметром Урок формирования знаний и умений  Аналитические методы решения логарифмических уравнений
Аналитические методы решения логарифмических уравнений Решение систем линейных уравнений (7 класс)
Решение систем линейных уравнений (7 класс) Свойства функции
Свойства функции Теорема Виета (8 класс)
Теорема Виета (8 класс) В лабиринте тригонометрических формул
В лабиринте тригонометрических формул Функция y=sinx. Свойства. Преобразование графиков
Функция y=sinx. Свойства. Преобразование графиков Презентация на тему Основные философские школы Древнего Китая
Презентация на тему Основные философские школы Древнего Китая  Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Свойства и график функции СИНУС
Свойства и график функции СИНУС Функции. Графики функций 7 класс
Функции. Графики функций 7 класс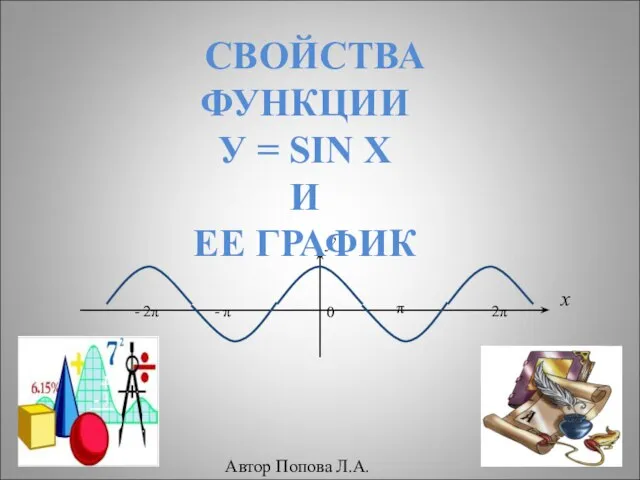 Свойства функции У = sin x и ее график
Свойства функции У = sin x и ее график