Функции и их графики 10 класс

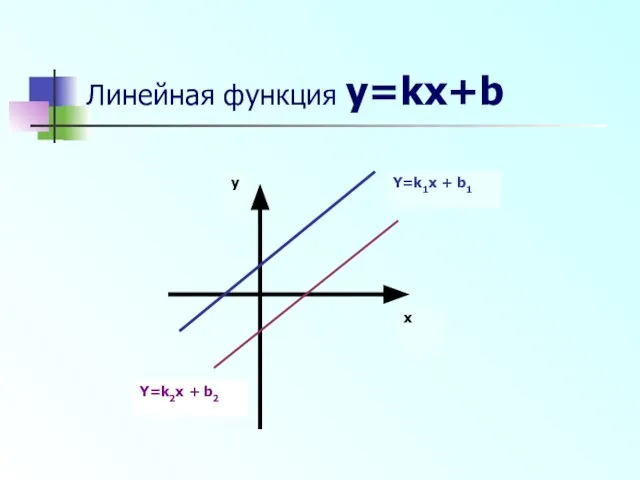
Линейная функция y=kx+b

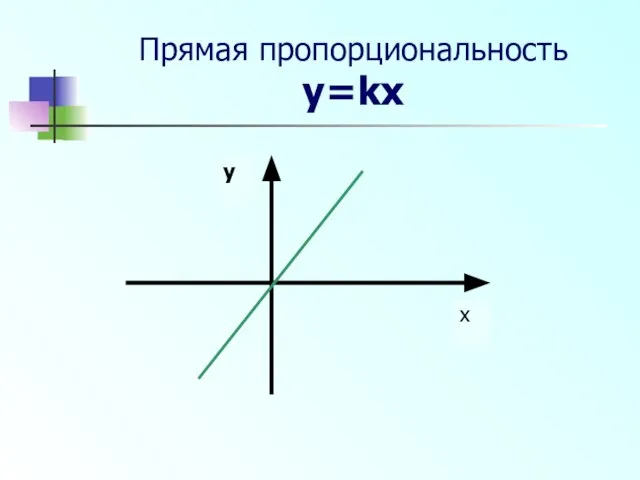
Прямая пропорциональность
y=kx

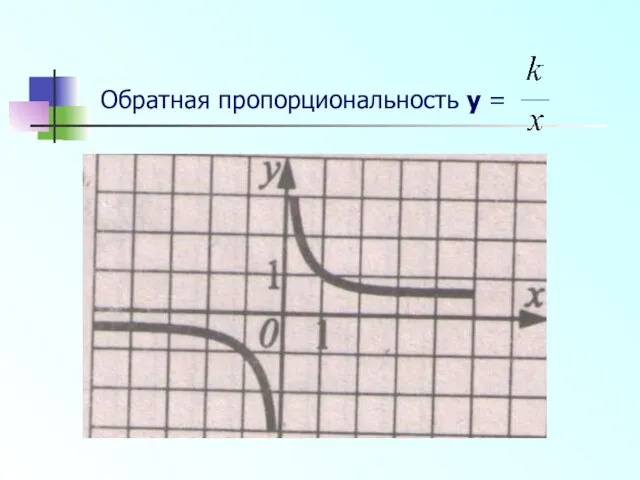
Обратная пропорциональность y =

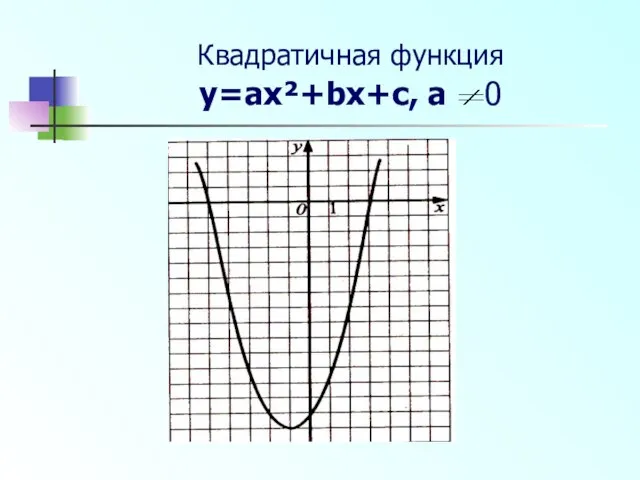
Квадратичная функция y=ax²+bx+c, a 0

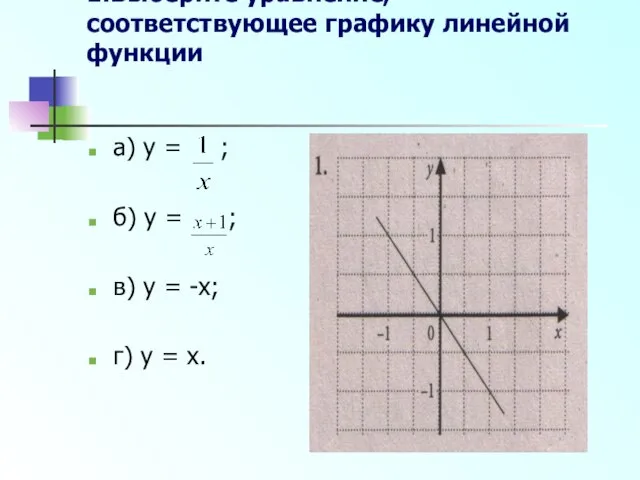
1.Выберите уравнение, соответствующее графику линейной функции
а) y = ;
б) y = ;
в) y = -x;
г) y = x.

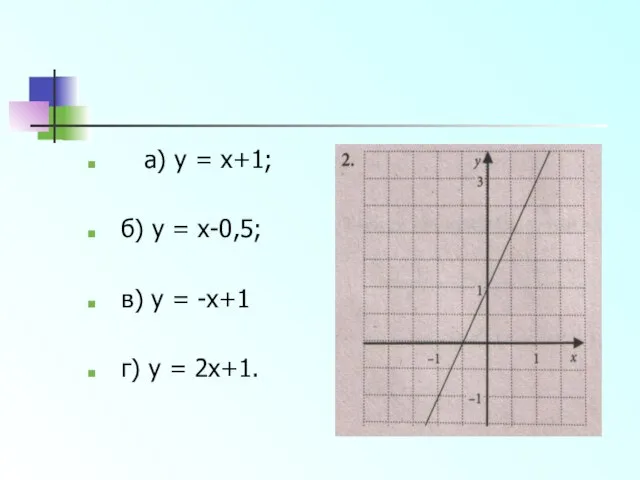
а) y = x+1;
б) y = x-0,5;
в) y = -x+1
г) y = 2x+1.

2. Определите точку, которая принадлежит графику функции, заданной уравнением y = 3x-2
а) А(3; 8); б) В(-2;10); в) С(0;0); г)D(1;1).

3. Линейная функция, заданная уравнением y = -5x+12, имеет угловой коэффициент, равный
а) 5; б) -5; в) 12; г)-12.

4. График функции, заданной уравнением y = -5x+7,4, параллелен графику функции, заданной уравнением
а) y = 5x+2; б) y = -5x-8;
в) y = 3x+7,4; г) y = 7,4x-5.

5. Определите промежутки, на которых квадратичные функции возрастают
а) (-6;∞)U(5;∞);
б) (-∞;1];
в) [1;∞);
г) [1;5].
а) [-6;-4];
б) (-∞;-4];
в) [-4;∞);
г) [1;5].

а) [8;11];
б) (-∞;5]U[11;∞);
в) [11;∞);
г) [8;∞).
а) (- ∞;-4]U[0;∞);
б) [-2;0);
в) [-2;∞);
г) [0;∞).

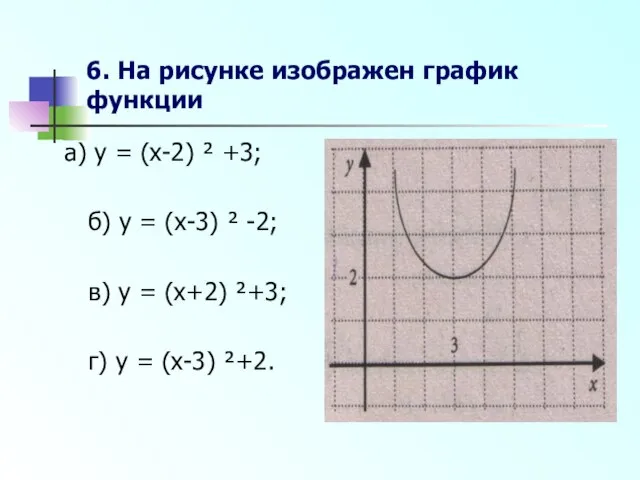
6. На рисунке изображен график функции
а) y = (x-2) ² +3;
б) y = (x-3) ² -2;
в) y = (x+2) ²+3;
г) y = (x-3) ²+2.

7. Графиком функции y=x³ является
а) прямая;
б) парабола;
в) кубическая парабола;
г) гипербола.

8. Четной является функция
а) y=3x-1;
б) y=x +4x;
в) y=3x ; г) y =.

9. Нечетной является функция
а) y=3x ;
б) y=x -x ;
в) y=(-x ²)³;
г) y =x .

Функция y=4x+2 принимает положительные значения на промежутке
а) (2;∞);
б) (-2;∞);
в) (0,5;∞);
г) (-0,5;∞).

Функция y=-3x+9 принимает положительные значения на промежутке
а) (-∞; ⅓);
б) (-∞; - ⅓);
в) (-∞; 3);
г) (-∞;-3).

На каком промежутке функция
y=-x²+8x-15 принимает отрицательные значения
а) (3;5); б) (-∞; 3)U(5;∞);
в) (-∞; 4]; г) [4;∞).

Известно, что прямая, перпендикулярная прямой y = 0,25x, касается параболы y=4x²+8x+7. Вычислите координаты точки касания.
(-1,5;4)

Известно, что прямая, параллельная прямой y = 3x-2, касается параболы y=2x²-3x+5. Вычислите координаты точки касания.
(1,5 ;5)

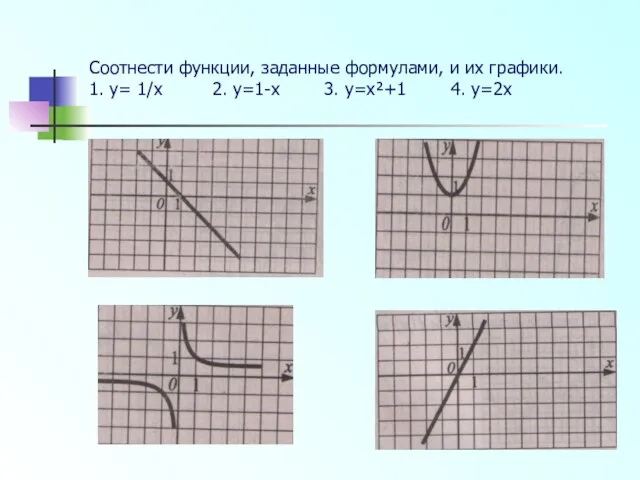
Соотнести функции, заданные формулами, и их графики.
1. y= 1/x 2. y=1-x 3. y=x²+1 4. y=2x

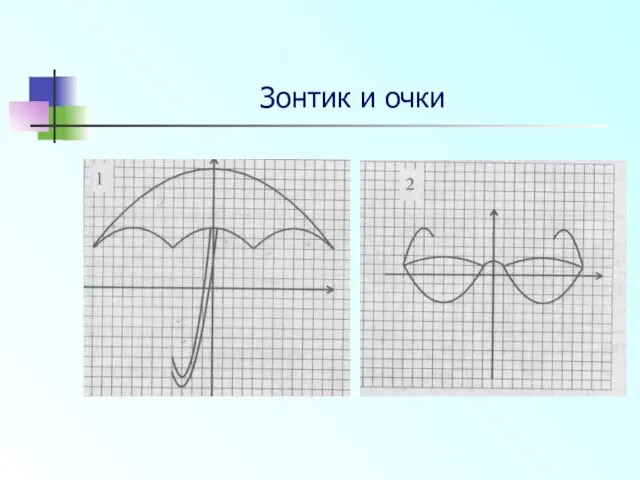
Зонтик и очки

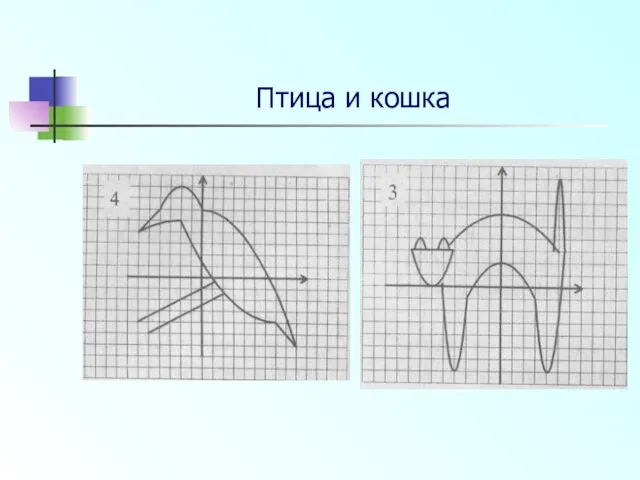
Птица и кошка

Домашнее задание
1 и 2 варианты.
1. Постройте график функции y = -x2+2x+3. При каких значениях аргумента выполняется неравенство 3≤y≤4?
2. Постройте график функции y= - . Сколько целых значений принимает данная функция, если -5≤х≤4?
3 вариант.
1. При каких значениях b и c вершина параболы y = x2+ b x+ c находится в точке
К(-4;7) ?
2. . При каких отрицательных значениях k прямая y=kx+10 и парабола y=-x2-3x+6 не имеют общих точек?