Содержание
- 2. Задачи урока Повторить и закрепить умения: Строить и читать графики степенной функции; Графически решать уравнения, неравенства,
- 3. Понятие функции. у = f(x) Укажите закон образования функций: у = 5х у = 2х3
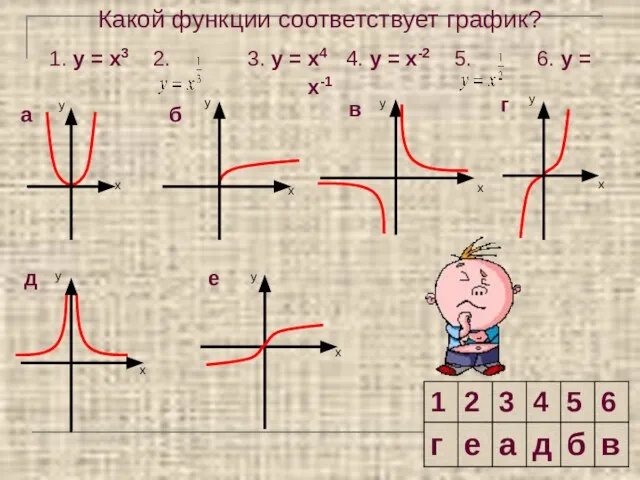
- 4. Какой функции соответствует график? 1. у = х3 2. 3. у = х4 4. у =
- 5. Найти область определения функции: а) (- ∞; 1,5); б)(- ∞; -4] ∪ (5;+∞) в)(- ∞; -2]
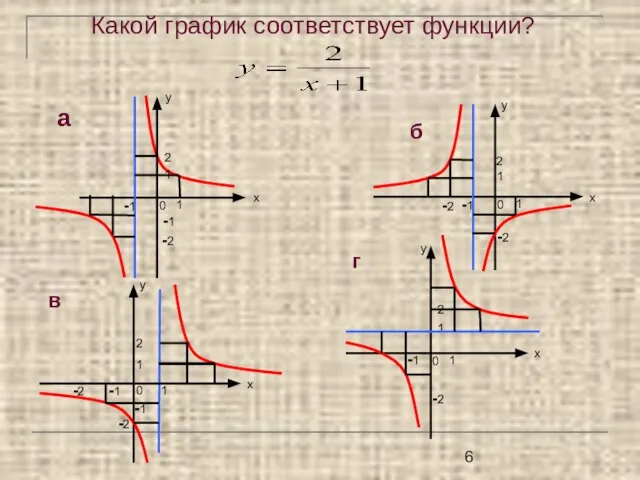
- 6. Какой график соответствует функции?
- 7. Какой график соответствует функции ?
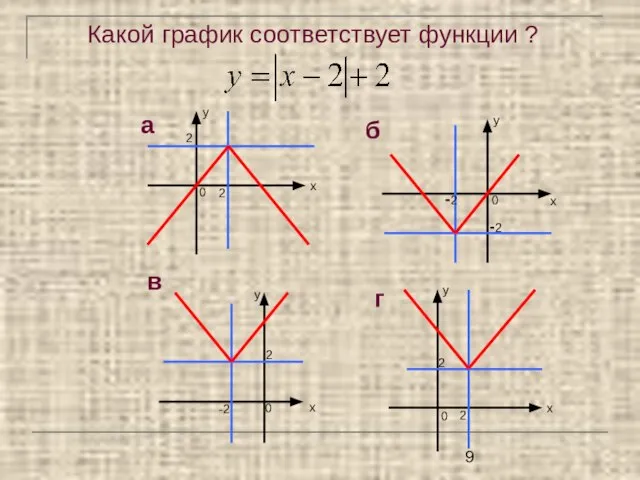
- 8. Какой график соответствует функции ?
- 9. Какой график соответствует функции ?
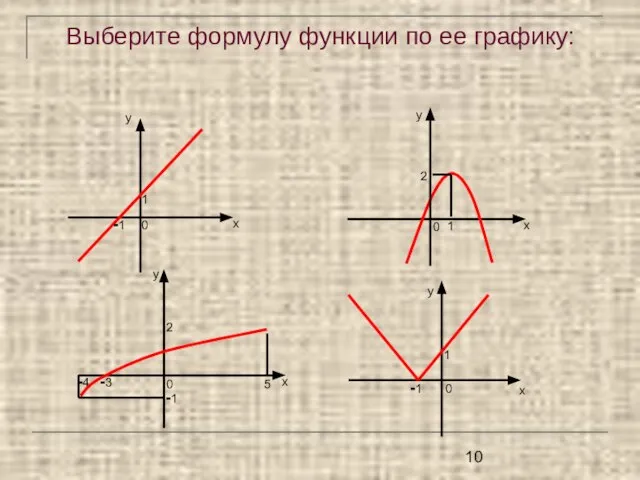
- 10. Выберите формулу функции по ее графику:
- 11. а) у = х - 1 б) у = х + 1 в) у = -х
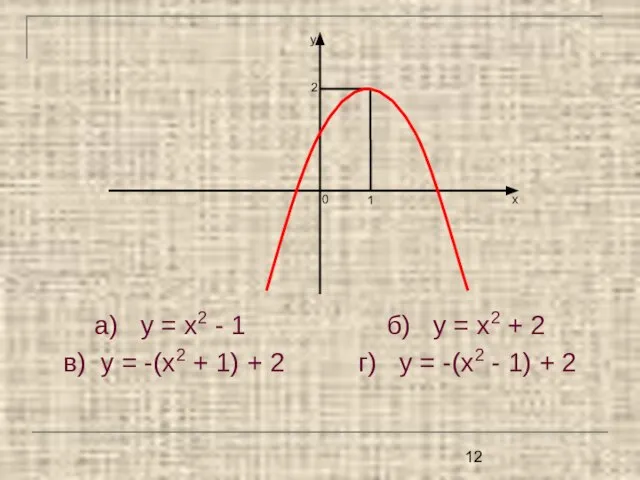
- 12. а) у = х2 - 1 б) у = х2 + 2 в) у = -(х2
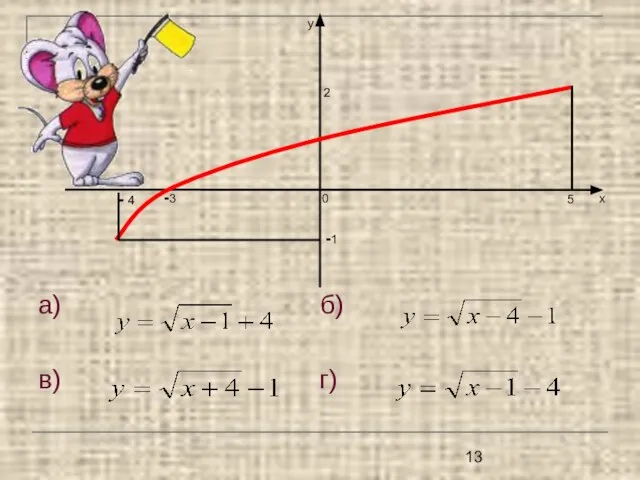
- 13. а) б) в) г) у - 4 -1 5 2 х -3 0
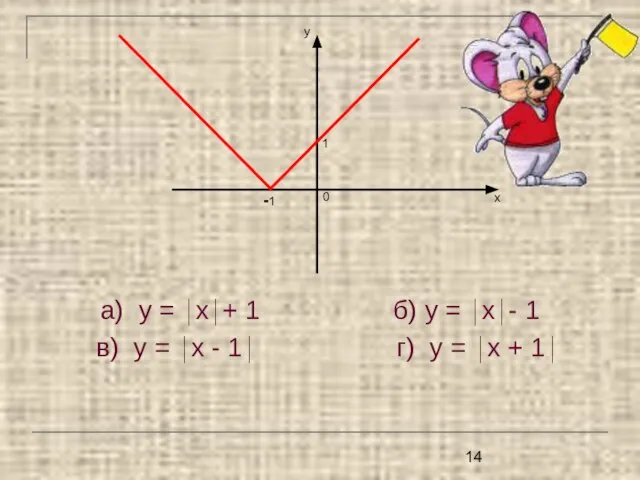
- 14. а) у = ⏐х⏐+ 1 б) у = ⏐х⏐- 1 в) у = ⏐х - 1⏐
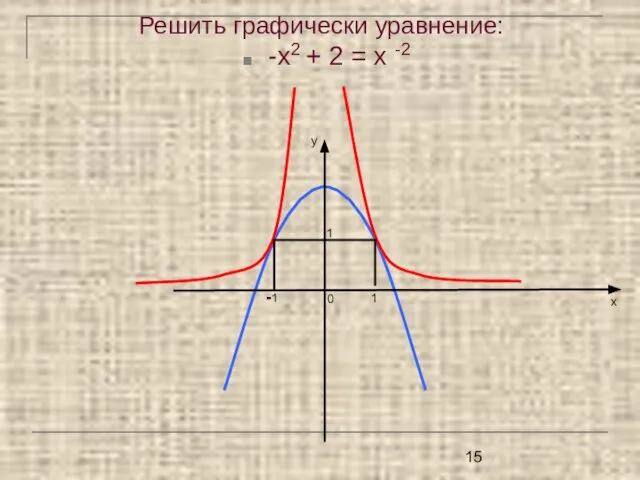
- 15. Решить графически уравнение: -х2 + 2 = х -2
- 16. Решить графически неравенство: у х -1 1 ////////////////////////////// /////////// 0
- 17. Определите число решений системы: у х 0
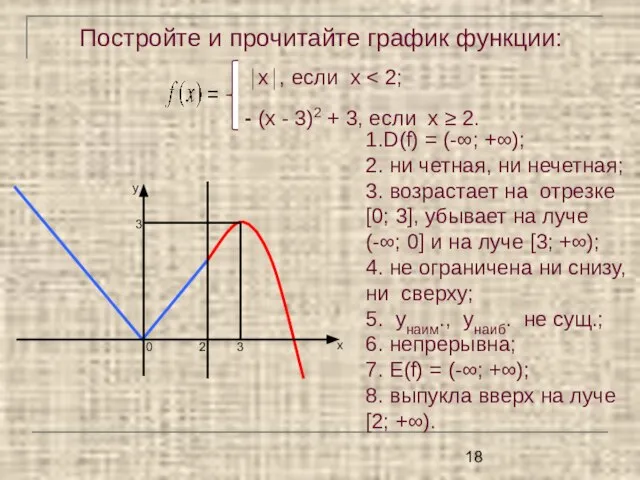
- 18. Постройте и прочитайте график функции: ⏐x⏐, если х 1.D(f) = (-∞; +∞); 2. ни четная, ни
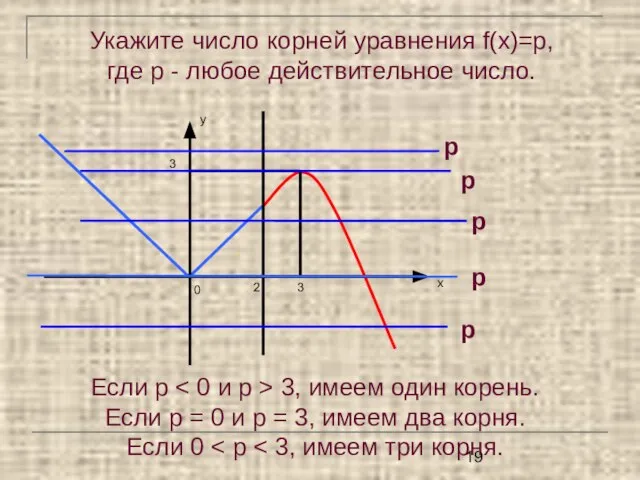
- 19. Укажите число корней уравнения f(x)=p, где p - любое действительное число. Если р 3, имеем один
- 20. Показать на графике область, удовлетворяющую системе неравенств: х2 + у2 ≥ 1, х2 + у2 ≤
- 22. Скачать презентацию


![Найти область определения функции: а) (- ∞; 1,5); б)(- ∞; -4] ∪](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304522/slide-4.jpg)


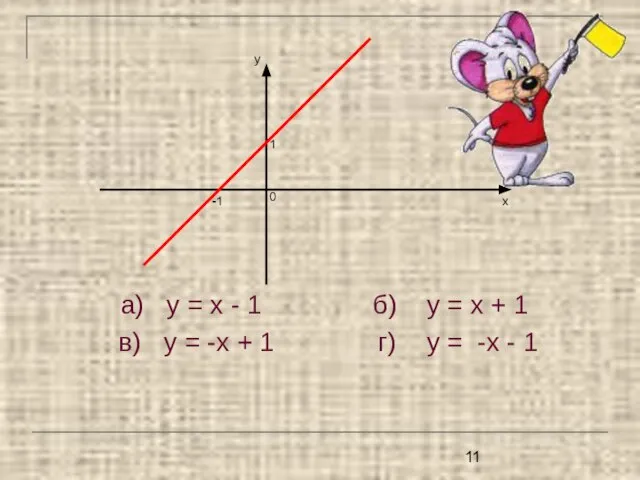



 Командировка в страну квадратных уравнений
Командировка в страну квадратных уравнений Обратные тригонометрические функции
Обратные тригонометрические функции Презентация на тему Классификация государственных служащих
Презентация на тему Классификация государственных служащих  Презентация на тему Порядок и особенности прохождения государственной службы в таможенных
Презентация на тему Порядок и особенности прохождения государственной службы в таможенных  Элементы алгебры
Элементы алгебры Презентация на тему Блиц - Опрос
Презентация на тему Блиц - Опрос  Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.
Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.  Презентация на тему спорт как альтернативу пагубным привычкам»
Презентация на тему спорт как альтернативу пагубным привычкам»  Pryamaya-proporcionalnost.ppt
Pryamaya-proporcionalnost.ppt Раскрываем секреты линейной функции и ее графика
Раскрываем секреты линейной функции и ее графика Алгебра 8 класс.
Алгебра 8 класс.  Формулы Виета и устное решение квадратных уравнений Кузнецова Лариса Викторовна учитель математики МБОУ СОШ №1 г. Климовск
Формулы Виета и устное решение квадратных уравнений Кузнецова Лариса Викторовна учитель математики МБОУ СОШ №1 г. Климовск  Степенная функция 9 класс учитель Ладошкина И.А.
Степенная функция 9 класс учитель Ладошкина И.А.  Презентация на тему Константин Васильев (Великоросс)
Презентация на тему Константин Васильев (Великоросс)  Презентация на тему Политика протекционизма
Презентация на тему Политика протекционизма  Комбинаторные задачи
Комбинаторные задачи Формулы для решения квадратного уравнения
Формулы для решения квадратного уравнения Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Нестандартно мыслим
Нестандартно мыслим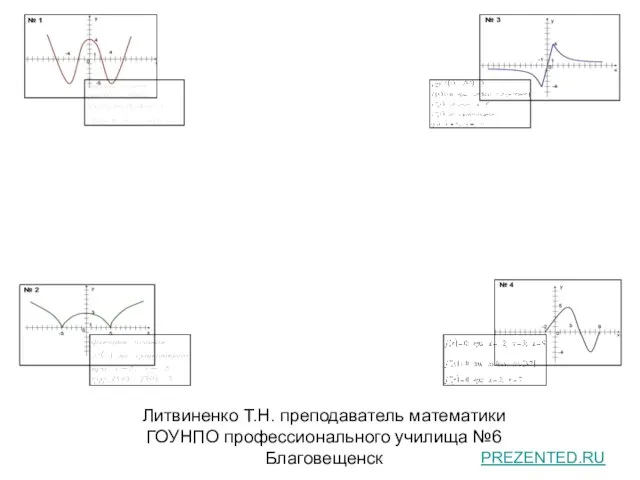 primenenie-proizvodnoy-funkcii.ppt
primenenie-proizvodnoy-funkcii.ppt Уравнения, содержащие знак модуля
Уравнения, содержащие знак модуля «Применение производной для исследования функции»
«Применение производной для исследования функции»  Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Касательная к графику функции
Касательная к графику функции ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Общие положения исследования неподлинной подписи
ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Общие положения исследования неподлинной подписи Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена 9-klass-kvadratichnaya-funkciya.ppt
9-klass-kvadratichnaya-funkciya.ppt Преобразования графиков квадратичной функции
Преобразования графиков квадратичной функции