Функция y= ІхІ

Актуальность – собрать сведения по теме в связи с подготовкой к экзамену
Проблема – в школьном курсе алгебры недостаточно задач с модулем
Объект исследования – функция
Предмет исследования – функция у=|x|
Цель – рассмотреть решение распространённых задач с модулем
Гипотеза – я предполагал, что задачи с модулем решаются только графически
Задачи –
1.Вспомнить известную мне информацию о задачах с модулем
2.Придумать новые задачи
3.Проконсультироваться с учителем
4.Создать презентацию
5.Защитить работу

Определение модуля
В математике через |x| обозначается абсолютная величина, или модуль числа х.
Абсолютная величина числа х равна этому числу, если х>0, равна противоположному числу –х, если x<0, и равна нулю, если х=0.
Таким образом, функция |x| определена для всех
х (-∞;+∞).
Множество её значений совпадает с множеством неотрицательных чисел.
х, если х≥0,
-х, если х<0.
|x|=

1.D(f)=(-∞;+∞)
2.E(f)=[0;+∞)
3.Ограничена снизу
4.Возрастает на[0;+∞)
убывает на(-∞;0]
5.Чётная функция
6.
7.Непрерывна
х
у
Свойства функции
График функции

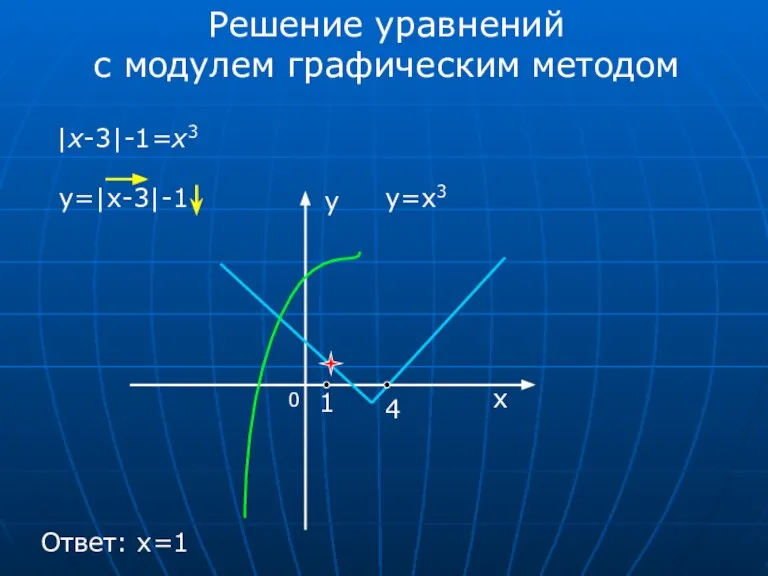
Решение уравнений
с модулем графическим методом
|x-3|-1=x3
y=|x-3|-1
y=x3
0
x
1
4
Ответ: x=1
у

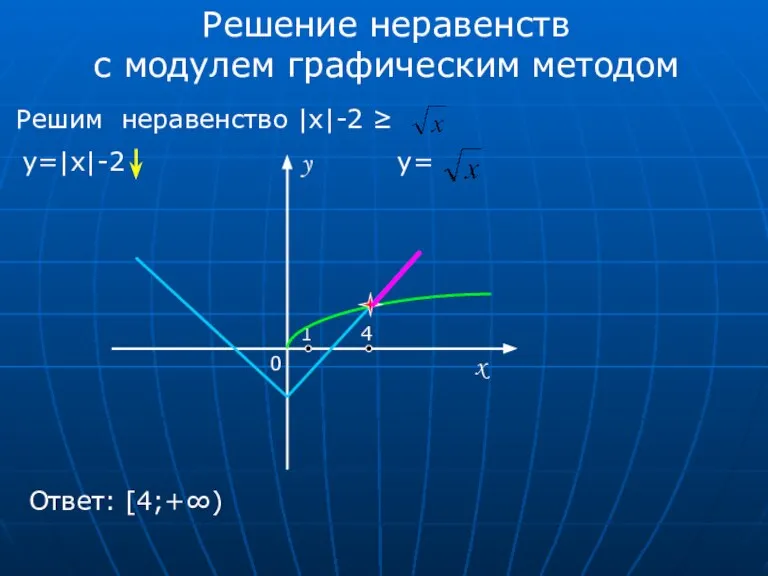
Решение неравенств
с модулем графическим методом
Решим неравенство |x|-2 ≥
y=|x|-2
y=
0
x
y
1
4
Ответ: [4;+∞)

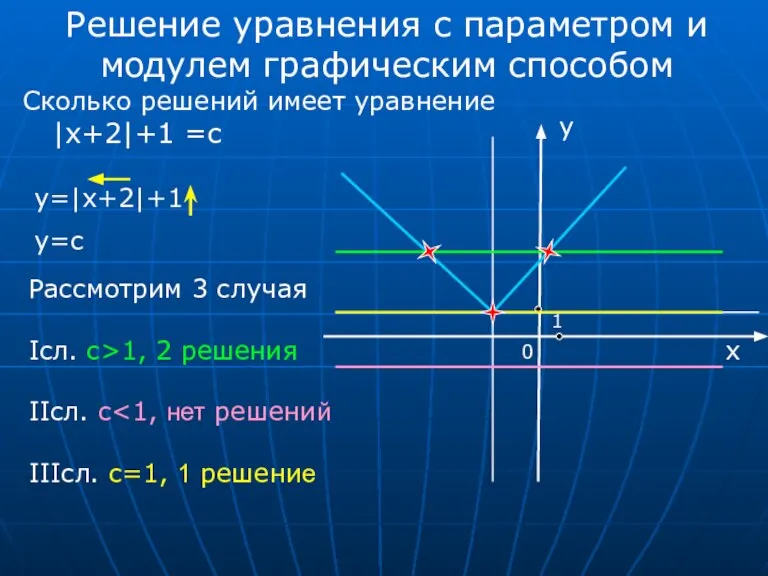
0
x
1
Решение уравнения с параметром и
модулем графическим способом
Рассмотрим 3 случая
Iсл. c>1, 2 решения
IIсл. c<1, нет решений
IIIсл. c=1, 1 решение
|x+2|+1 =c
y=|x+2|+1
y=c
у
Сколько решений имеет уравнение

Аналитический метод решения уравнения с модулем
Решим уравнение|x-3|=5
I способ
Рассмотрим два случая
1 случай
x-3≥0
x-3=5
x=5+3
x=8, 8-3≥0 (и)
2 случай
x-3<0
3-x=5
-x=5-3
x=-2, -2-3<0 (и)
Ответ:-2, 8
II способ
x-3=5 или x-3=-5
x=8 x=-2

Алгоритм решения уравнений с модулем
Найти нули модулей.
Отметить нули на координатной прямой.
Решить уравнение на каждом из промежутков с помощью системы.
Написать ответ.

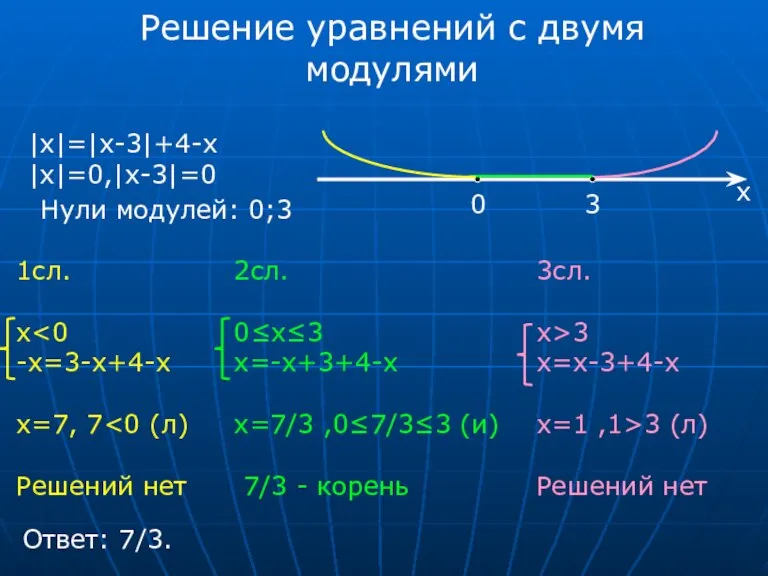
Решение уравнений с двумя модулями
|x|=|x-3|+4-x
|x|=0,|x-3|=0
Нули модулей: 0;3
0
3
х
1сл.
x<0
-x=3-x+4-x
x=7, 7<0 (л)
Решений нет
2сл.
0≤x≤3
x=-x+3+4-x
x=7/3 ,0≤7/3≤3 (и)
7/3 - корень
3сл.
x>3
x=x-3+4-x
x=1 ,1>3 (л)
Решений нет
Ответ: 7/3.

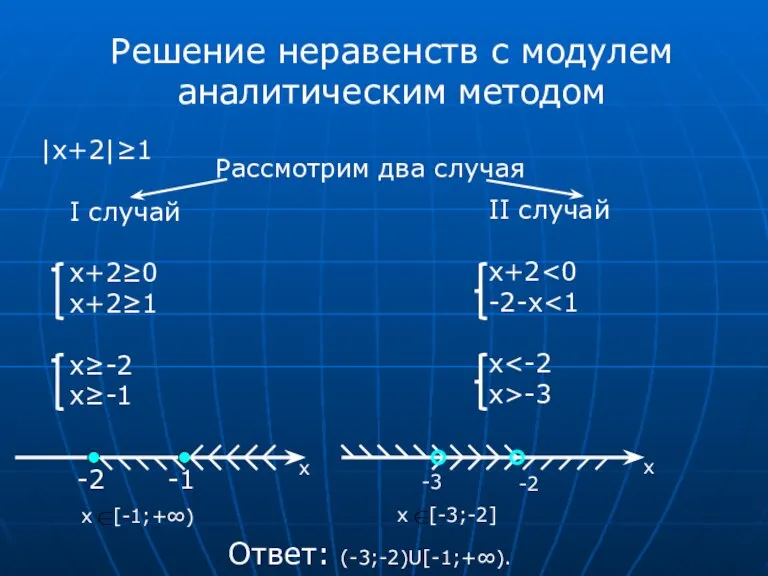
Решение неравенств с модулем аналитическим методом
|x+2|≥1
Рассмотрим два случая
I случай
x+2≥0
x+2≥1
x≥-2
x≥-1
II случай
x+2<0
-2-x<1
x<-2
x>-3
Ответ: (-3;-2)U[-1;+∞).
-2
-1
x
x [-1;+∞)
-3
-2
x
x [-3;-2]

Решение неравенств с модулем различными методами
Третий способ. Имеем: |x-2.5|>2.
Геометрически выражение |x-2.5| означает расстояние р(x-2.5)
на координатной прямой между точками х и 2.5. Значит, нам нужно
Найти все такие точки х, которые удалены от точки 2.5 более, чем на 2-
это точки из промежутков (-∞;0.5) и (4.5;+∞)
Итак, получили следующее решения неравенства: х<0.5;x>4.5.
Четвёртый способ.
Поскольку обе части заданного неравенства неотрицательны,
то возведение их в квадрат есть равносильное преобразование
неравенства. Получим |2x-5|2>42
Воспользовавшись тем что |x|2=x2, получим
(2x-5-4)(2x-5+4)>0
Применив метод интервалов получим тот же ответ.

Алгоритм решения неравенств с модулем
Найти нули модулей.
Отметить нули на координатной прямой.
Решить неравенство на каждом из промежутков с помощью системы.
Написать ответ.

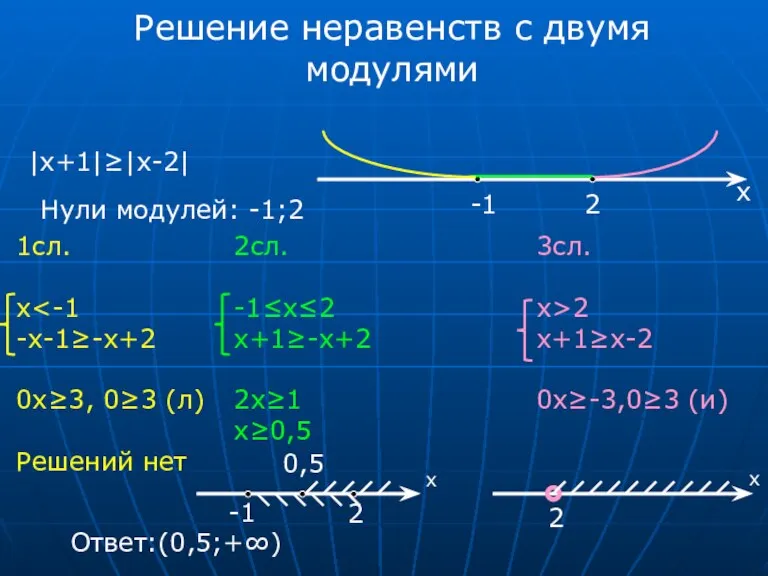
Решение неравенств с двумя модулями
|x+1|≥|x-2|
Нули модулей: -1;2
-1
2
х
1сл.
x<-1
-x-1≥-х+2
0x≥3, 0≥3 (л)
Решений нет
2сл.
-1≤x≤2
х+1≥-x+2
2х≥1
х≥0,5
3сл.
x>2
х+1≥х-2
0x≥-3,0≥3 (и)
Ответ:(0,5;+∞)
-1
2
х
0,5
2
х

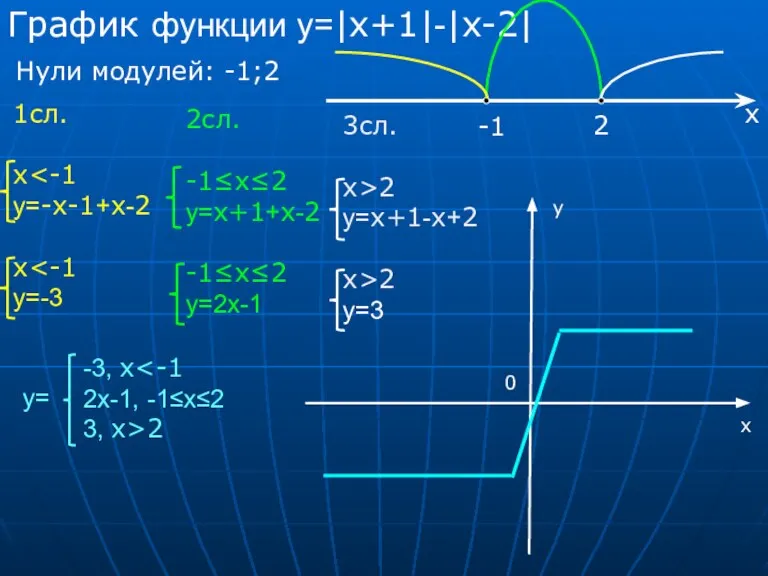
График функции у=|x+1|-|x-2|
Нули модулей: -1;2
1сл.
x<-1
у=-x-1+х-2
x<-1
у=-3
2сл.
-1≤x≤2
у=х+1+x-2
-1≤x≤2
у=2х-1
3сл.
x>2
у=х+1-х+2
x>2
у=3
-3, x<-1
2х-1, -1≤x≤2
3, x>2
х
у
0
у=

Выводы
В ходе работы над проектом моя гипотеза не подтвердилась.
Я не только вспомнил графический способ, но и научился решать уравнения и неравенства аналитическим методом и строить графики с несколькими модулями.
В дальнейшем можно рассмотреть аналитический метод решения неравенств и уравнений с модулем и параметром.