Алгебра высказываний. Основные операции алгебры высказываний

ВОПРОСЫ
1. Что такое логика? Формальная логика. Математическая логика.
2. Этапы развития логики.
3. Применение математической логики.
4. Алгебра высказываний. Простые и сложные высказывания.
5. Основные операции алгебры высказываний.

ВОПРОС №1
Что такое логика?
Формальная
логика
Математическая логика

LOGOS (ГРЕЧ.)- СЛОВО, ПОНЯТИЕ, РАССУЖДЕНИЕ, РАЗУМ
СЛОВО «ЛОГИКА» ОБОЗНАЧАЕТ СОВОКУПНОСТЬ ПРАВИЛ, КОТОРЫМ ПОДЧИНЯЕТСЯ ПРОЦЕСС МЫШЛЕНИЯ.
ОСНОВНЫМИ ФОРМАМИ АБСТРАКТНОГО МЫШЛЕНИЯ ЯВЛЯЮТСЯ: ПОНЯТИЯ, СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ.

ПОНЯТИЕ - ФОРМА МЫШЛЕНИЯ, В КОТОРОЙ
ОТРАЖАЮТСЯ СУЩЕСТВЕННЫЕ ПРИЗНАКИ
ОТДЕЛЬНОГО ПРЕДМЕТА ИЛИ КЛАССА
ОДНОРОДНЫХ ПРЕДМЕТОВ. (ТРАПЕЦИЯ, ДОМ)
СУЖДЕНИЕ - МЫСЛЬ, В КОТОРОЙ ЧТО-ЛИБО УТВЕРЖДАЕТСЯ ИЛИ ОТРИЦАЕТСЯ О ПРЕДМЕТАХ. (ВЕСНА НАСТУПИЛА, И ГРАЧИ ПРИЛЕТЕЛИ)
УМОЗАКЛЮЧЕНИЕ - ПРИЕМ МЫШЛЕНИЯ, ПОСРЕДСТВОМ КОТОРОГО ИЗ ИСХОДНОГО ЗНАНИЯ ПОЛУЧАЕТСЯ НОВОЕ ЗНАНИЕ.
(ВСЕ МЕТАЛЛЫ - ПРОСТЫЕ ВЕЩЕСТВА)

МАТЕМАТИЧЕСКАЯ ЛОГИКА - ИЗУЧАЕТ ЛОГИЧЕСКИЕ СВЯЗИ И ОТНОШЕНИЯ, ЛЕЖАЩИЕ В ОСНОВЕ ЛОГИЧЕСКОГО (ДЕДУКТИВНОГО) ВЫВОДА.
ЛОГИКА (ФОРМАЛЬНАЯ) - НАУКА О ЗАКОНАХ И ФОРМАХ ПРАВИЛЬНОГО МЫШЛЕНИЯ.

ВОПРОС №2
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ

АРИСТОТЕЛЬ (384-322 гг. до н.э.) - ОСНОВОПОЛОЖНИК ЛОГИКИ
КНИГИ:
«КАТЕГОРИИ»
«ПЕРВАЯ АНАЛИТИКА»
«ВТОРАЯ АНАЛИТИКА»
(ИССЛЕДОВАЛ РАЗЛИЧНЫЕ ФОРМЫ РАССУЖДЕНИЙ , ВВЕЛ ПОНЯТИЕ СИЛЛОГИЗМА)

СИЛЛОГИЗМ - РАССУЖДЕНИЕ, В
КОТОРОМ ИЗ ЗАДАННЫХ ДВУХ
СУЖДЕНИЙ ВЫВОДИТСЯ ТРЕТЬЕ.
1. ВСЕ МЛЕКОПИТАЮЩИЕ ИМЕЮТ СКЕЛЕТ. ВСЕ КИТЫ - МЛЕКОПИТАЮЩИЕ. СЛЕДОВАТЕЛЬНО, ВСЕ КИТЫ ИМЕЮТ СКЕЛЕТ.
2. ВСЕ КВАДРАТЫ - РОМБЫ. ВСЕ РОМБЫ - ПАРАЛЛЕЛЕГРАММЫ. СЛЕДОВАТЕЛЬНО, ВСЕ КВАДРАТЫ - ПАРАЛЛЕЛОГРАММЫ.

АРИСТОТЕЛЬ ВЫДЕЛИЛ ВСЕ ПРАВИЛЬНЫЕ
ФОРМЫ СИЛЛОГИЗМОВ, КОТОРЫЕ МОЖНО
СОСТАВИТЬ ИЗ РАССУЖДЕНИЙ ВИДА: - «Все А суть В»
- «Некоторые А суть В»
- «Все А не суть В»
- «Некоторые А не суть В»
Логика, основанная на теории
силлогизмов называется классической.

Декарт Рене (1596-1650, фр. философ, математик)
РЕКОМЕНДОВАЛ В ЛОГИКЕ ИСПОЛЬЗОВАТЬ МАТЕМАТИЧЕСКИЕ МЕТОДЫ.

Лейбниц Г.В. (1646-1716, нем. ученый и математик) -
Предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной системы счисления.
Логика обретает символьный язык, конкретность законов, распространяется за рамки гуманитарных наук.

Джордж Буль (1815-1864, анл.) - основоположник мат. логики.
1847 г. –Джордж Буль в работе «Математический анализ логики» изложил основы булевой алгебры.
РАЗРАБОТАЛ АЛФАВИТ, ОРФОГРАФИЮ И ГРАММАТИКУ.
1815 – 1864 гг. благодаря трудам математика Дж. Буля появился раздел математической логики, получивший название алгебры логики или булевой алгебры.

ВКЛАД В СТАНОВЛЕНИЕ И РАЗВИТИЕ МАТ. ЛОГИКИ:
АУГУСТУС ДЕ МОРГАН (1806 - 1871)

ВКЛАД В СТАНОВЛЕНИЕ И РАЗВИТИЕ МАТ. ЛОГИКИ:
УИЛЬЯМ СТЕНЛИ ДЖЕВОНС (1835 - 1882) ПЛАТОН СЕРГЕЕВИЧ ПОРЕЦКИЙ (1846-1907)
ЧАРЛЗ САНДЕРС ПИРС (1839-1914)

ВОПРОС №3
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Логика оказала влияние на развитие математики, прежде всего теории множеств, функциональных систем, алгоритмов, рекурсивных функций.
2) В гуманитарных науках
(логика,
криминалистика).
3) Математическая логика является средством для изучения деятельности мозга - для решения этой самой важной проблемы биологии и науки вообще.

1938 г. – американский математик и инженер Клод Шеннон связал Булеву алгебру (аппарат математической логики), двоичную систему кодирования и релейно-контактные переключательные схемы, заложив основы будущих ЭВМ.
4) Идеи и аппарат логики используется в кибернетике, ВТ и электротехнике (построены компьютеры на основе законов математической
логики).

5) Идеи и аппарат логики используется в программировании, базах данных и экспертных системах.
PROLOG – язык логического программирования

ВОПРОС №4
Алгебра высказываний
Простые и сложные высказывания

АЛГЕБРА ЛОГИКИ (ВЫСКАЗЫВАНИЙ) -
РАЗДЕЛ МАТЕМАТИЧЕСКОЙ ЛОГИКИ, ИЗУЧАЮЩИЙ ВЫСКАЗЫВАНИЯ И ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД НИМИ.

ВЫСКАЗЫВАНИЕ - ЭТО ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ, О КОТОРОМ МОЖНО СКАЗАТЬ, ЧТО ОНО ИСТИННО ИЛИ ЛОЖНО.
1) Земля - планета Солнечной системы.
2) 2+8<5
3) 5 •5=25
4) Всякий квадрат есть параллелограмм
5) Каждый параллелограмм есть квадрат
6) 2•2 =5

ВЫСКАЗЫВАНИЕМ
НЕ ЯВЛЯЕТСЯ:
1) ВОСКЛИЦАТЕЛЬНЫЕ И ВОПРОСИТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ.
2) ОПРЕДЕЛЕНИЯ.
3) ПРЕДЛОЖЕНИЯ ТИПА: «ОН СЕРОГЛАЗ»
«X2-4X+3=0»

ВЫСКАЗЫВАНИЕ, КОТОРОЕ МОЖНО РАЗЛОЖИТЬ НА ЧАСТИ, БУДЕМ НАЗЫВАТЬ СЛОЖНЫМ, А НЕРАЗЛОЖИМОЕ ДАЛЕЕ ВЫСКАЗЫВАНИЕ - ПРОСТЫМ.
1) На улице идет дождь. (А)
2) На улице идет дождь. (В)
3) На улице светит солнце и на улице идет дождь. (А и В)
4) На улице светит солнце или на улице идет дождь. (А или В)
А≡1; В≡0

ВОПРОС №5
ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ

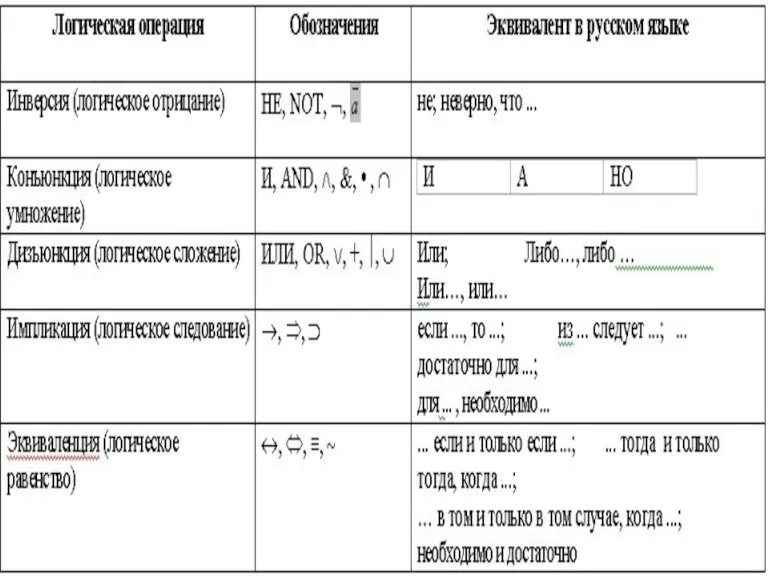
ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ) - ПРИСОЕДИНЕНИЕ ЧАСТИЦЫ «НЕ» К СКАЗУЕМОМУ ДАННОГО ПРОСТОГО ВЫСКАЗЫВАНИЯ ИЛИ ПРИСОЕДИНЕНИЕ СЛОВ «НЕВЕРНО ЧТО. . .» КО ВСЕМУ ВЫСКАЗЫВАНИЮ.
ИНВЕРСИЯ ЛОГИЧЕСКОЙ ПЕРЕМЕННОЙ ИСТИННА, ЕСЛИ САМА ПЕРЕМЕННАЯ ЛОЖНА, И, НАОБОРОТ, ИНВЕРСИЯ ЛОЖНА, ЕСЛИ ПЕРЕМЕННАЯ ИСТИННА.

ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) -
СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В ОДНО С ПОМОЩЬЮ СОЮЗА «ИЛИ»,
УПОТРЕБЛЯЕМОГО В НЕИСКЛЮЧАЮЩЕМ ВИДЕ.
ДИЗЪЮНКЦИЯ ДВУХ
ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ
ЛОЖНА ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОБА ВЫСКАЗЫВАНИЯ
ЛОЖНЫ.

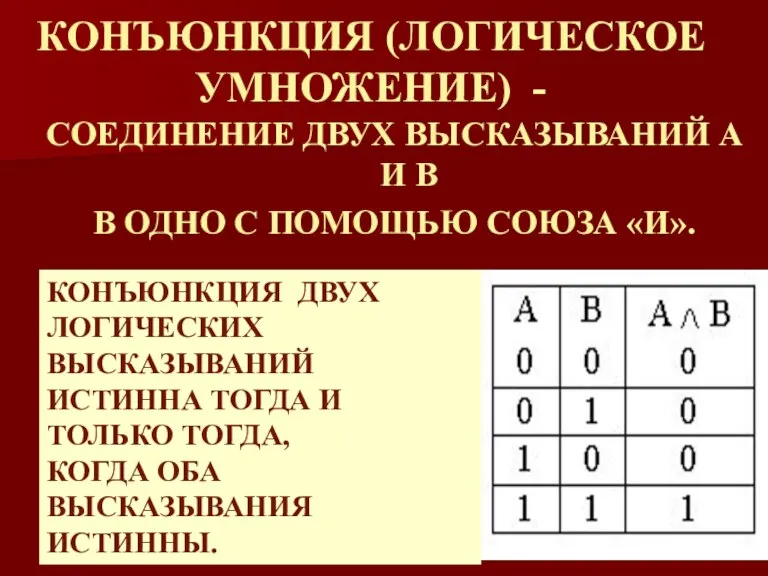
КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) -
СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В
В ОДНО С ПОМОЩЬЮ СОЮЗА «И».
КОНЪЮНКЦИЯ ДВУХ
ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ
ИСТИННА ТОГДА И ТОЛЬКО ТОГДА,
КОГДА ОБА ВЫСКАЗЫВАНИЯ
ИСТИННЫ.

ИМПЛИКАЦИЯ -
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ
«ЕСЛИ . . . , ТО . . .»
ИМПЛИКАЦИЯ ВЫСКАЗЫВАНИЙ
ЛОЖНА ЛИШЬ В СЛУЧАЕ, КОГДА А
ИСТИННО, А В ЛОЖНО.

ЭКВИВАЛЕНЦИЯ -
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И ТОЛЬКО ТОГДА, КОГДА …»
ЭКВИВАЛЕНЦИЯ ДВУХ
ВЫСКАЗЫВАНИЙ ИСТИННА В ТОМ И ТОЛЬКО ТОМ СЛУЧАЕ, КОГДА ОБА ЭТИ
ВЫСКАЗЫВАНИЯ ИСТИННЫ ИЛИ ЛОЖНЫ.

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ:
ИНВЕРСИЯ;
КОНЪЮНКЦИЯ;
ДИЗЪЮНКЦИЯ;
ИМПЛИКАЦИЯ И ЭКВИВАЛЕНТНОСТЬ.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить логической формулой.
Всякая логическая переменная и символы «истина» («1») и «ложь» («0»)- формулы.
Если А и В – формулы, то «не А», «А и В», «А или В», «если А, то В», «тогда и только тогда А, когда В» - формулы.
Никаких других формул в алгебре логики нет.