НЕРАВЕНСТВА (8 КЛАСС)

Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района
Республики Коми
Мишариной Альбиной
Геннадьевной

СОДЕРЖАНИЕ
Линейные неравенства
Квадратные неравенства

Линейные неравенства
(8 класс)

Математику нельзя изучать,
наблюдая как это делает сосед.

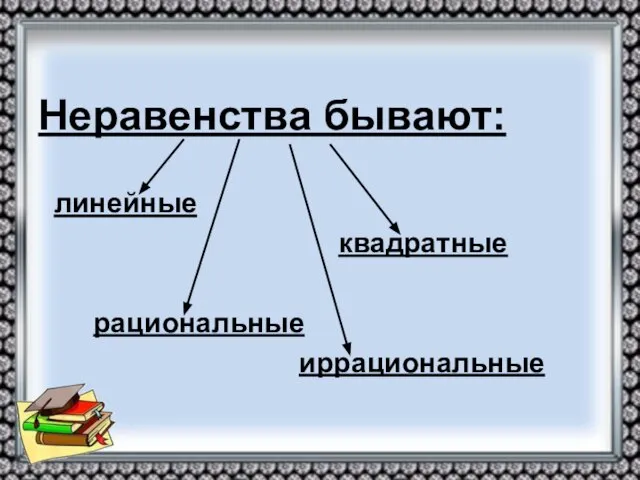
Неравенства бывают:
линейные
квадратные
рациональные
иррациональные

Вспомним:

Изобразите на координатной прямой промежуток
(работаем в парах):
1) [-2;4]
2) (-3;3) 3) (3;+∞)
4) (-∞;4]
5) (-5;+∞)
6) (0;7]
а) х≥2
в) х≤3
с) х>8
д) х<5
е) -4<х<7
ж) -2≤х<6

Линейные неравенства
Определения:
Запись вида а>в; а≥в или а<в; а≤в называется неравенством
Неравенства вида а≥в, а≤в называются
нестрогими.
Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной называется то значение переменной, которое обращает его в верное числовое
неравенство

Линейные неравенства
Правила:
1) Любой член неравенства можно переносить из одной части неравенства в другую, изменив его знак на противоположный, при этом знак неравенства не изменится.

Линейные неравенства
Правила:
2) Обе части неравенства можно умножить или разделить на одно и тоже положительное число, при этом знак неравенства не изменится.

Линейные неравенства
Правила:
3) Обе части неравенства можно умножить или разделить на одно и тоже отрицательное число, при этом знак неравенства изменится на противоположный.

Решим неравенство: 16х>13х+45
Решение:
16х-13х > 45 слагаемое 13х с противоположным знаком перенесли в левую часть неравенства
3х > 45 привели подобные слагаемые
х > 15 поделили обе части неравенства на 3
15 х
Ответ: (15;+∞)

Решить неравенство:
2х + 4 ≥ 6
2х ≥ -4 + 6 2х ≥ 2
х ≥ 1
х
1
Ответ: [1;+∞).

Решить неравенства в парах:
1) х+2 ≥ 2,5х-1;
2) х- 0,25(х+4)+0,5(3х-1) > 3;
3) х²+х < х(х-5)+2;

Проверим:
х+2 ≥ 2,5х-1
Решение:
х-2,5х ≥ -2 -1
- 1,5х ≥ - 3 х ≤ 2
2 х
Ответ: (-∞;2]
2) х²+х < х(х-5)+2
Решение:
х²+х < х²- 5х +2
х² +х - х²+5х < 2
6х < 2
х < ⅓
⅓ х
Ответ: (-∞;⅓)

Самостоятельная работа по вариантам: решить неравенства
Вариант 1.
1) 3х≤21
2) -5х<35
3) 3х+6≤3
4) 2-6х>14
5) 3-9х≤1-х
6) 5(х+4)<2(4х-5)
Вариант 2.
1) 2х≥18
2) -4х>16
3) 5х+11≥1
4) 3-2х<-1
5) 17х-2≤12х-1
6) 3(3х-1)>2(5х-7)

Проверим ответы:
Вариант 1.
1) (-∞;7]
2) (7;∞)
3) (-∞;-1]
4) (-∞;-2)
5) [0,25;∞)
6) (10;∞)
Вариант 2.
1) [9;∞)
2) (-∞;-4)
3) [-2;∞)
4) (2;∞)
5) (-∞;0,5]
6) (-∞;9)

Самостоятельная работа
Найдите наименьшее целое число, являющееся решением неравенства:
1) 2(х-3)-1-3(х-2)-4(х+1) < 0;
2) 0,2(2х+2)-0,5(х-1)<2

Проверим:
1)
2(х-3)-1-3(х-2)-4(х+1) < 0
2х -6-1-3х+6-4х-4 < 0
-5х < 5
х > -1
-1 х
Ответ: 0
2)
0,2(2х+2)-0,5(х-1)<2 0,4х +0,4 -0,5х +0,5 <2
-0,1х < -0,9 +2
-0,1х < +1,1
х > 11
11 х
Ответ: 12

Решаем сами:
Найдите наименьшее натуральное число, являющееся решением неравенства 3х-3 < х+4
Решение: 3х – х < 3+4
2х < 7
х < 3,5
0 3,5 х
Ответ: 1

КВАДРАТНЫЕ
НЕРАВЕНСТВА
(8 класс)

Математику нельзя изучать,
наблюдая как это делает сосед.

Квадратные неравенства
Определение: Квадратным называется
неравенство, левая часть которого −
квадратный трёхчлен, а правая часть
равна нулю:
ах²+bх+с>0 ах²+bх+с≥0
ах²+bх+с<0 ах²+bх+с≤0

Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство
Решить неравенство − это значит найти все его решения или установить, что их нет.

Являются ли следующие неравенства квадратными?
А) 4у² - 5у +7 > 0 Б) 2х - 4 > 0
В) 4х² - 2х ≥ 0
Г) 3у – 5у² + 7 < 0
Д) 4 – 6х + 5х² ≤ 0
Е) 5у⁴ +3у - 6 < 0

Основные способы решения квадратных неравенств:
Метод интервалов
Графический метод

Запомним:
Чтобы решить квадратное неравенство ах²+вх+с >0 методом интервалов надо:
1) Найти корни соответствующего
квадратного уравнения ах²+вх+с = 0;
2) Корни уравнения нанести на числовую ось;
3) Разделить числовую ось на интервалы;
3) Определить знаки функции в каждом из интервалов;
4) Выбрать подходящие интервалы и
записать ответ.

Решим квадратное неравенство методом интервалов:
Дано неравенство: х² + х – 6 ≥ 0
Решение: 1) решим соответствующее квадратное уравнение х² + 5х – 6 = 0.
Т.к. а+в+с=0, то х₁ =1, а х₂ = - 6
2)
-6 1 х
3) Запишем ответ:
(-∞; -6]U[1; +∞)
+
+
-

Работаем в парах:
Решить неравенства:
1) х²-3х<0;
2) х²-4х>0;
3) х²+2х≥0;
4) -2х²+х+1≤0
Проверим ответы:
(0;3)
(-∞;0)U(4;+∞)
(-∞; -2]U[0; +∞)
(-∞; - 0,5]U[1; +∞)

Решите неравенства методом интервалов самостоятельно:
Решить неравенства
1) х(х+7)≥0;
2) (х-1)(х+2)≤0;
3) х- х²+2<0;
4) -х²-5х+6>0;
5) х(х+2)<15
Проверим ответы:
1) (-∞;-7]U[0; +∞)
2) [-2;1]
3) (-∞;-1)U(2; +∞)
4) (-6;1)
5) (-5;3)

Графический метод решения квадратного неравенства:
1).Определить направление ветвей параболы, по знаку первого коэффициента квадратичной функции.
2).Найти корни соответствующего квадратного уравнения;
3). Построить эскиз графика и по нему
определить промежутки, на которых
квадратичная функция принимает
положительные или отрицательные
значения

Например:
Решить графически неравенство х²+5х-6≤0
Решение: рассмотрим у = х²+5х-6,
это квадратичная функция, графиком является парабола, т.к. а=1, то ветви направлены вверх.
у
+ +
-6 1 x
Ответ: [-6;1]
-

Решите графически неравенства
в парах:
1) х²-3х<0;
2) х²-4х>0;
3) х²+2х≥0;
4) -2х²+х+1≤0
Проверим ответы:
(0;3)
(-∞;0)U(4;+∞)
(-∞; -2]U[0; +∞)
(-∞; - 0,5]U[1; +∞)

Всем
СПАСИБО
ЗА УРОК!!!