Алгебраические дроби Основное свойство дроби Сокращение дробей

«In die bruche kommen» (нем., буквально: «попасть в дроби»
Мишка! Ты это о чем? Куда попасть? Зачем попасть?
У немцев есть такая поговорка «Попасть в дроби», что означает попасть в тупик, в трудное положение.
Мишка! А почему?
Долгое время действия с дробными числами считались очень сложными.
Мишка! А мы же уже изучали дроби! Помнишь?
Да, помню! Но сегодня мы познакомимся с другими дробями.

Я эту дробь знаю!

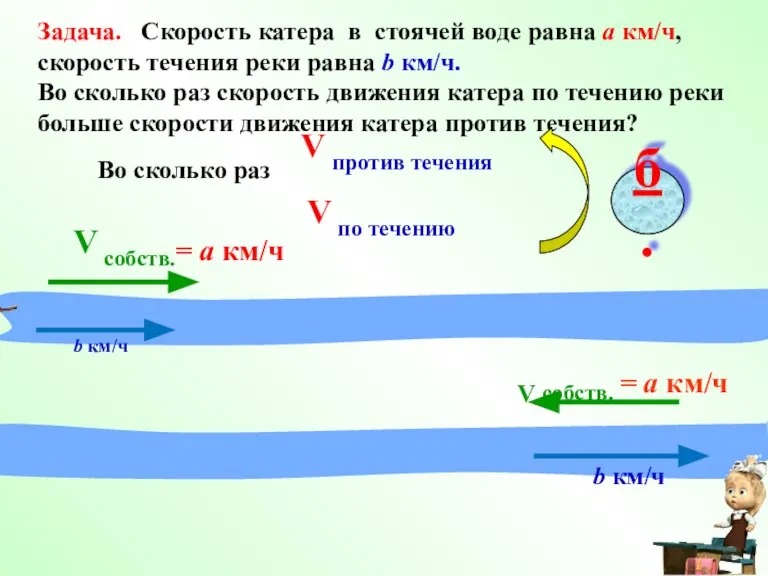
Задача. Скорость катера в стоячей воде равна а км/ч,
скорость течения реки равна b км/ч.
Во сколько раз скорость движения катера по течению реки
больше скорости движения катера против течения?
V собств.
= a км/ч
b км/ч
V собств.
= a км/ч
b км/ч
Во сколько раз
б.
V по течению
V против течения

Решение.
Скорость катера по течению равна (a + b) км/ч
Скорость катера против течения равна (a – b) км/ч
Скорость катера по течению в
раз больше, чем против течения.
Выражение называют алгебраической дробью;
(a + b) - числитель дроби,
(a – b) - знаменатель дроби.

Если вместо букв, входящих в алгебраическую дробь,
подставить некоторые числа, то получится значение
этой алгебраической дроби.
при a = 12, b = 4
Примеры алгебраических дробей

Буквы могут принимать лишь допустимые
значения, т. е. такие значения, при которых
знаменатель этой дроби не равен нулю.
Для дроби допустимыми
являются все значения а, кроме а = 0 и а = 1.
Найти допустимые значения букв, входящих в дробь:

Найти допустимые значения букв,
входящих в дробь:
любое действительное число

Основное свойство дроби можно записать так:
b ≠ 0, m ≠ 0, тогда
При умножении или делении числителя и знаменателя
алгебраической дроби на одно и то же число, не равное
нулю, получается равная ей дробь
Основное свойство дроби
Я это знаю!
Правильно! А с новыми дробями так:
Я же это знаю! Это сокращение дроби!
Можно сокращать алгебраическую дробь на общий множитель числителя и знаменателя дроби

Разложите на множители:

Найдите ошибки:
Мишка, Мишка!
Помоги мне ошибки найти!

Сократите дроби:

Сократите дроби:

Мишка, Мишка!
Расскажи, расскажи!
Что ты знаешь об этих алгебраических дробях?
Давай спросим ребят!

А правда, что выражение вида называют алгебраической дробью.
В алгебраической дроби числитель и знаменатель- алгебраические выражения.
Основное свойство дроби можно записать так: , где b≠0, m≠0
Допустимыми значениями букв, входящих в алгебраическую дробь называют такие значения, при которых числитель этой дроби не равен нулю
Сократить дробь можно, если числитель и знаменатель дроби представлены в виде произведения.
(a-b)²=(a-b) (a+b)
Одним из способов разложения многочленов на множители является применение формул сокращенного умножения

Восстановите, частично стёртые записи:
Ой-ой-ой…

К каждой дроби найти равную ей дробь,
используя соответствие число - буква
.
1)
2)
3)
а)
б)
в)
.
Так, так…

К каждой дроби найти равную ей дробь,
используя соответствие число - буква
.
1)
2)
3)
а)
б)
в)
.
1)
в)
2)
а)
3)
б)

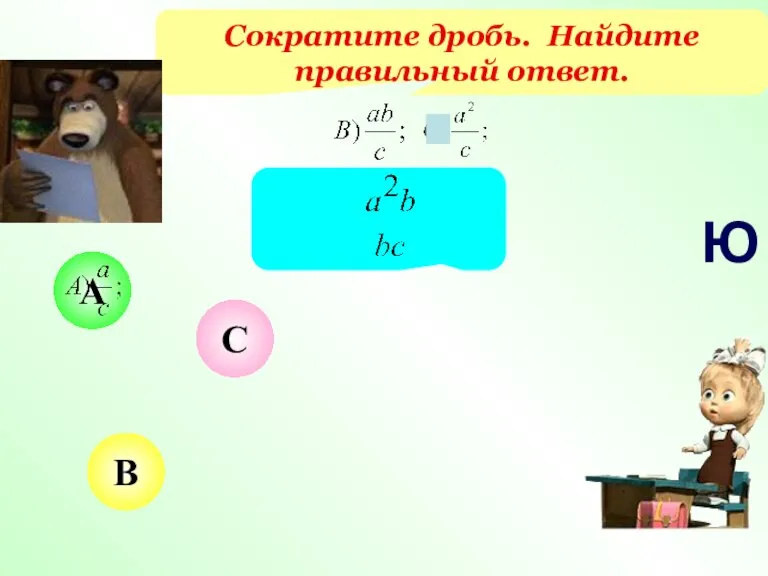
Сократите дробь. Найдите правильный ответ.
В
А
С
Ю

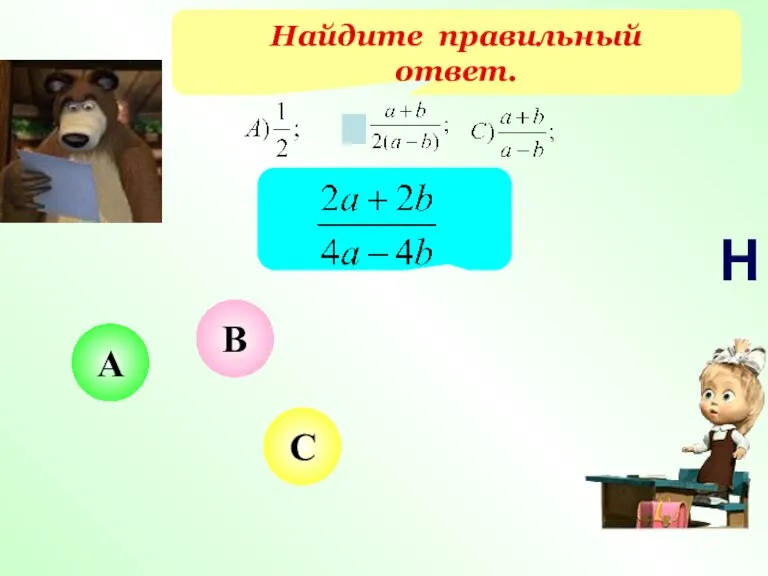
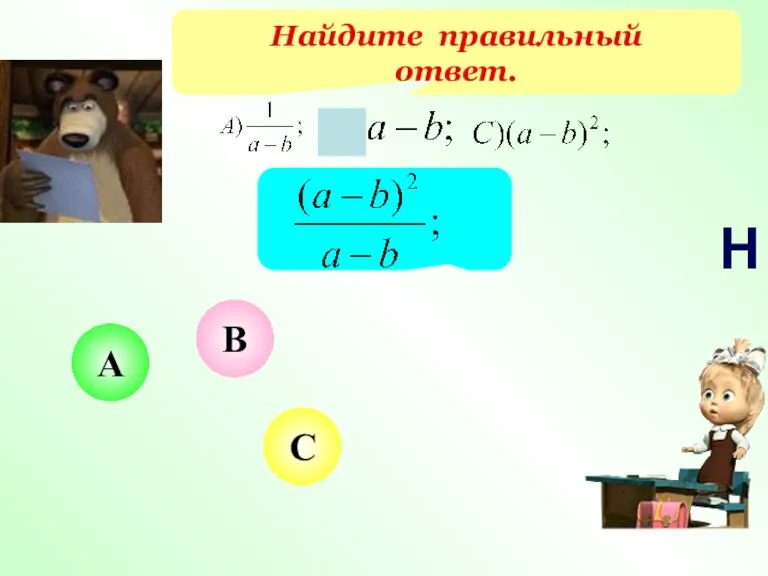
Найдите правильный
ответ.
С
А
В
Н

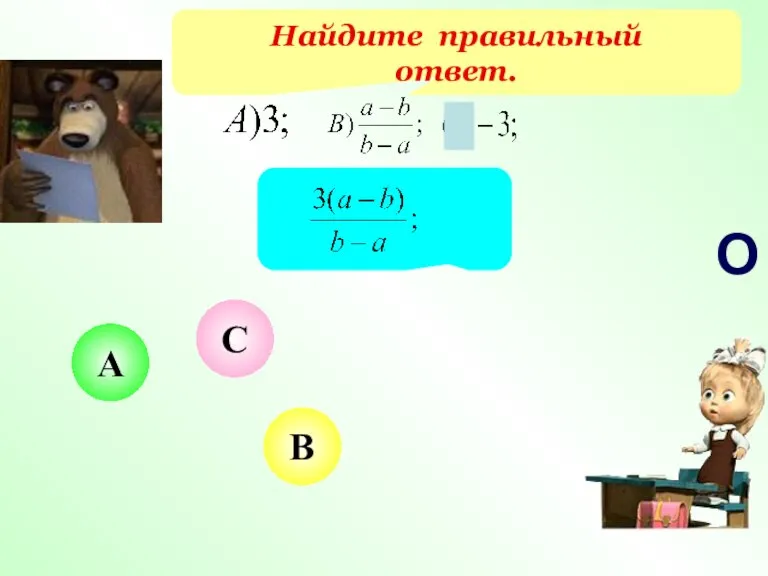
Найдите правильный
ответ.
В
А
С
О

Найдите правильный
ответ.
С
А
В
Н

Найдите правильный
ответ.
С
В
А
Т

Сократите дробь. Найдите правильный ответ.
В
А
С
Ь

Сэр Исаак Ньютон - родился 4 января 1643 года в деревне Вулсторп (графство Линкольншир), Англия. Великий английский физик, математик и астроном. Автор фундаментального труда «Математические начала натуральной философии», в котором он описал закон всемирного тяготения и так называемые Законы Ньютона, заложившие основы классической механики. Разработал дифференциальное и интегральное исчисление, теорию цветности и многие другие математические и физические теории.
Н
Ь
Ю
Т
О
Н

Физкультминутка
1.Приведите дробь к знаменателю, равному:
б)16х
а) 12
в)24ab
2.Найдите допустимые значения букв:
а)
Если знаешь ты ответ, - смело потянись.
Посмотри налево ты, - соседу улыбнись.
Если же ответа нет, руки ты потри,
И соседа справа ты о помощи проси!
ТЕСТ

Найдите значение алгебраической дроби, предварительно сократив ее:
при х=10,
х=0,
х=5,
х=2.
Всегда ли это возможно?
Когда нет?

Ой, сколько я всего узнала…
Спасибо, ребята!
Вы мне очень помогли!
Итоги урока