Квадратный корень из произведения

Цели урока:
Повторить определение арифметического квадратного корня.
Ввести и доказать теорему о квадратном корне из произведения.
Научиться находить квадратный корень из произведения.
Проверить знания и умения с помощью самостоятельной работы.

Квадратный корень из произведения
План урока:
Актуализация знаний.
Изучение нового материала.
Закрепление формулы на примерах.
Самостоятельная работа.
Подведение итогов.
Задание на дом.

Здравствуйте, ребята!
Повторим :
2. Что называется арифметическим
квадратным корнем из числа
3. При каком значении
выражение
имеет смысл?
1. Как называется выражение

Найдите:
1)
2)
3)
7
или
или
7

Сегодня мы познакомимся с одним из свойств арифметического квадратного корня.
Введем и докажем теорему о квадратном корне из произведения, рассмотрим примеры её применения.
Затем Вам будут предложены задания для самопроверки.
Желаю удачи!

Рассмотрим арифметический корень
Найдите значение выражения:
Значит,
Итак, корень из произведения двух чисел равен
произведению корней из этих чисел.
Попробуем решить

Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Если
то
Теорема

Квадратный корень из произведения
Доказательство:
значит,
- имеют смысл.
4. Вывод:
(т.к. произведение двух неотрицательных чисел неотрицательно)‏
5. Итак,

Мы рассмотрели доказательство теоремы об извлечении квадратного корня из произведения.
Перейдём к практической работе.
Сейчас я вам покажу как применяется эта формула при решении примеров.
Решайте вместе со мной.

Вычислите значение квадратного корня, используя
теорему о корне из произведения:
Решаем примеры:

Решаем примеры:
2. Найдите значение выражения:

Быстрый счёт
А я догадался, как можно использовать эту формулу для быстрых вычислений.
Смотри и учись.

Вариант 1
Вариант 2
Предлагаю вам примеры для самостоятельного решения:

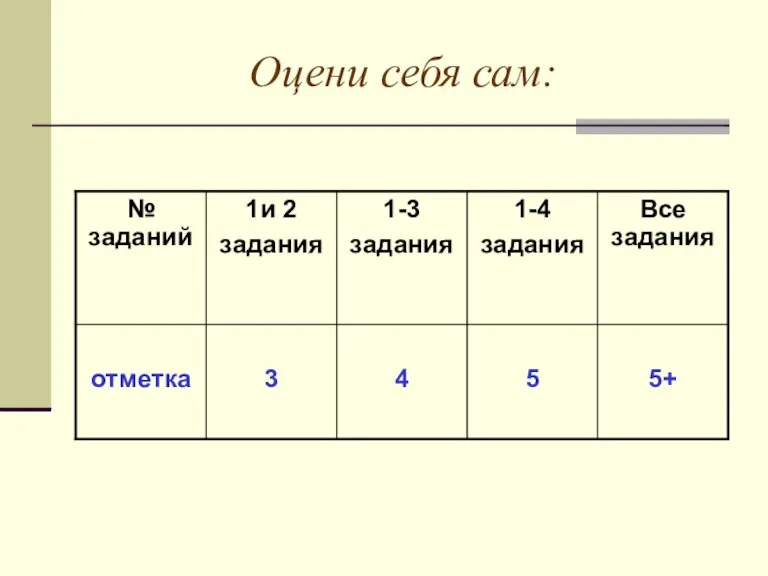
Оцени себя сам:

Подведем итоги
С какой теоремой мы сегодня познакомились?
Сформулируйте правило извлечения квадратного корня из произведения?
Когда пользуемся этим правилом?

Задание на дом:
№ 359(а,б),
361(а,б),
363(а,б),
365(а,в).