В6 элементы теории вероятностей

Теоретические основы
http://www.ege-study.ru/ege-materials/math/probability.html
http://le-savchen.ucoz.ru/index/0-65
События
Классическое определение вероятности
Прототипы задач ЕГЭ 2013 с решениями
http://mathege.ru

Немного о событиях
Событие – все, что происходит или не происходит в реальной жизни.
Случайное событие – событие, которое в ходе испытания (опыта) может произойти, а может и не произойти.
Несовместные события – события, которые не могут произойти одновременно.
Событие, противоположное событию А, состоит в том, что в результате испытания событие А не произошло. Обозначение: Ā

Вероятность
Наступление того или иного случайного события происходит с некоторой вероятностью.
Вероятностью P случайного события A называют отношение числа всех благоприятных исходов m испытания к общему числу n всех исходов
Сумма вероятностей противоположных событий равна 1
Р(А) + Р(Ā) = 1

Например,
бросают монету (проводят испытание). Возможны два случая (исхода): монета упала орлом (случайное событие), монета упала решкой (случайное событие).
Эти события несовместные, так как одновременно монета выпасть орлом и решкой не может.
Если монета не выпала орлом, значит, она выпала решкой. Эти события противоположные.
Найдем вероятность того, что монета выпала орлом. Всего исходов n = 2, благоприятный исход (монета выпала орлом) m = 1. Р = 1/2
Вероятность того, что монета выпала решкой, определяется аналогично и равна ½.
Так как события противоположные, то сумма вероятностей этих событий равна 1.
1/2 + ½ = 1

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение.
В результате бросания первой кости возможны 6 исходов: выпадение 1, 2, 3, 4, 5, 6 очков. Для каждого из них возможны еще по шесть исходов при бросании второй кости. Общее количество исходов
n= 6*6= 62=36
8 очков можно получить в следующих случаях :
Количество благоприятных
исходов m= 5
Вероятность по определению
равна P = 5/36 = 0,138… ≈ 0,14

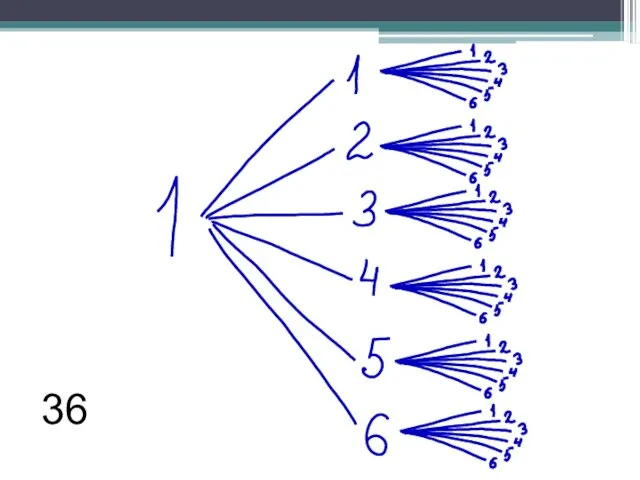
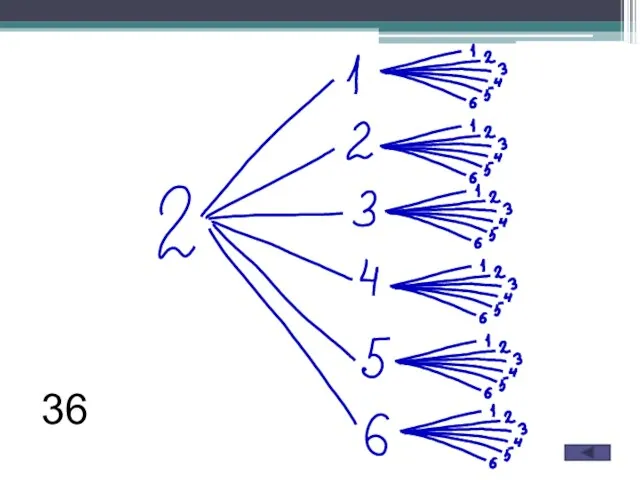
Задание B6 (№ 283443)
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Решение.
Найдем общее количество исходов n. Для первой кости возможно 6 исходов – появление 1,2,3,4,5,6 очков, для каждого из которых по 6 при бросании второй и третьей кости, т.е.
n = 6*6*6 = 63= 216
Найдем количество благоприятных исходов m.
16 очков можно получить следующими способами:
4 6 6 6 4 6 6 6 4 5 5 6 5 6 5 6 5 5
m = 6
Р = 6/216 =0,027… ≈ 0,03

36

36

Задание B6 (№ 283469)
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Задачу можно переформулировать – бросают две симметричные монеты одновременно.
Монета может выпасть орлом или решкой, всего два исхода. При бросании 2 монет общее количество исходов n = 2*2 = 22= 4.
о о о р р о о о
Орел может выпасть ровно один раз в 2 случаях, т.е. благоприятных исходов m = 2
Р = 2/4 = 0,5

Задание B6 (№ 283467)
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Решение.
Задачу можно переформулировать – бросают три симметричные монеты одновременно.
Монета может выпасть орлом или решкой, всего два исхода. При бросании 3 монет общее количество исходов n = 2*2*2 = 8.
ооо оор оро орр роо рро рор ррр
Орел может выпасть ровно два раза в 3 случаях, т.е. благоприятных исходов m = 3
Р = 3/8 = 0,375

Задание B6 (№ 283471)
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
Решение.
Общее количество исходов n = 2*2*2*2 = 24= 16.
Орел не выпадет ни разу, если все 4 раза выпадет решка. Это возможно в одном случае, т.е. благоприятных исходов m = 1
Р = 1/16 = 0,0625

Задание B6 (№ 283479)
В чемпионате по гимнастике участвуют 50 спортсменок: 24 из США, 13 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Решение.
Общее количество спортсменок n = 50
Благоприятные исходы – спортсменка из Канады
m = 50 – 24 - 13 = 13
P= 13/50 = 0, 26
Замечание. В данной задаче не учитывается, какой по счету окажется выступающая спортсменка

Задание B6 (№ 283727)
В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 8 спортсменов из Сербии, 3 спортсмена из Хорватии и 6 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Сербии.
Решение.
Общее количество спортсменов n = 3+8+3+6 = 20
Спортсменов из Сербии m = 8
Р = 8/20 = 0,4

Задание B6 (№ 286121)
На семинар приехали 3 ученых из Швейцарии, 5 из Голландии и 4 из Франции. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что шестым окажется доклад ученого из Швейцарии.
Решение аналогично предыдущей задачи
Порядок выступления не учитывается при решении.

Задание B6 (№ 285929)
Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 16 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение (аналогично)
Общее количество докладов n = 40
На третий день запланировано (40-16):2=12 докладов, т.е. m = 12
P= 12/40 = 0,3

Задание B6 (№ 286211)
Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 участников из России, в том числе Ярослав Исаков. Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким-либо теннисистом из России?
Решение.
Ярослав Исаков может сыграть в паре с любым из 46 - 1 = 45 участников. Т. е. n = 45
Среди них 19 - 1 = 18 пар, в которых Ярослав Исаков сыграет с теннисистом из России. Т.е. m = 18
Р = 18/45 = 0,4

Задание B6 (№ 286239)
В сборнике билетов по математике всего 20 билетов, в 11 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам.
Решение.
Всего билетов n = 20
Вопрос по логарифмам содержится в 11 из них. m=11
Вероятность того, что вопрос по логарифмам достанется ученику равна
Р=11/20=0,55

Задание B6 (№ 286317)
В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.
Решение.
Всего билетов n = 35
Билетов, которые не содержат вопрос по кислотам
35 - 7 = 28 , т.е. m=28
Вероятность того, что вопроса по кислотам
не достанется ученику равна
Р=28/35=0,8
Задачу можно решить по другому.
Речь идет о противоположных событиях. Поэтому сумма их вероятностей равна 1.
Найдем вероятность того, что в билетах содержится вопрос по кислотам
Р1 = 7/35 = 1/5 = 0,2
Вероятность того, что выбранный билет не содержит вопрос по кислотам
Р = 1- Р1 = 1 - 0,2 = 0,8

Задание B6 (№ 283579)
В среднем из 1400 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение.
Всего поступило в продажу насосов n = 1400
Насосов, которые не подтекают 1400 – 7 = 1393, т.е. m=1393
Вероятность того, что насос не подтекает равна
Р=1393/1400=0,995
Задачу можно решить по другому.
Речь идет о противоположных событиях. Поэтому сумма их вероятностей равна 1.
Найдем вероятность того, что выбранный насос подтекает
Р1 = 7/1400=1/200=0,005
Вероятность того, что выбранный насос не подтекает равна
Р = 1- Р1 = 1 - 0,005 = 0,995

Задание B6
Фабрика выпускает сумки. В среднем из 120 сумок девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной.
Решение.
Всего сумок n = 120
Качественных сумок (благоприятные исходы) 111, т.е. m=120-9=111
Вероятность того, что сумка окажется качественной равна
Р=111/120=0,925
Другой способ
Р1 = 9/120 = 0,075
Р = 1 – 0,075 = 0,925