Содержание
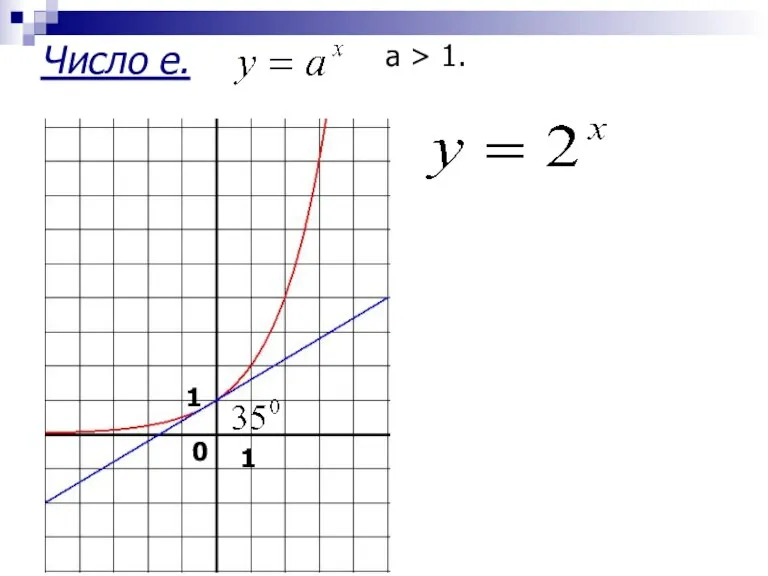
- 2. Число e. а > 1. 1 1 0
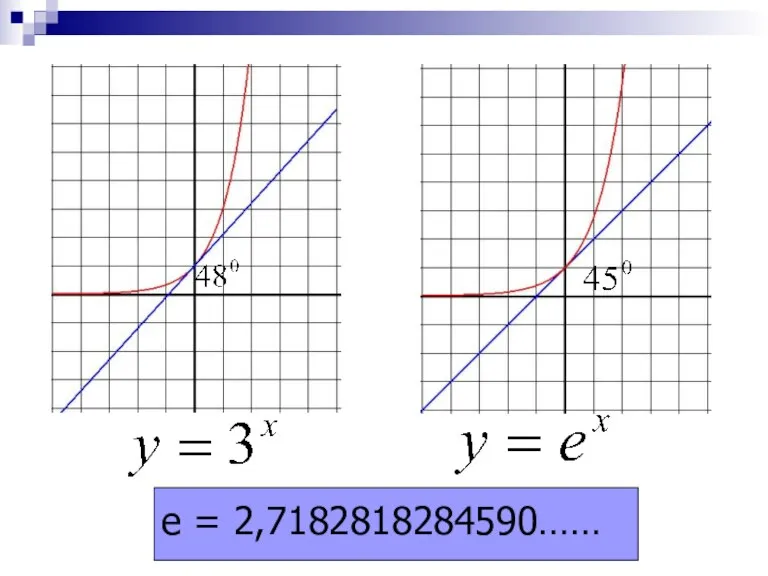
- 3. e = 2,7182818284590……
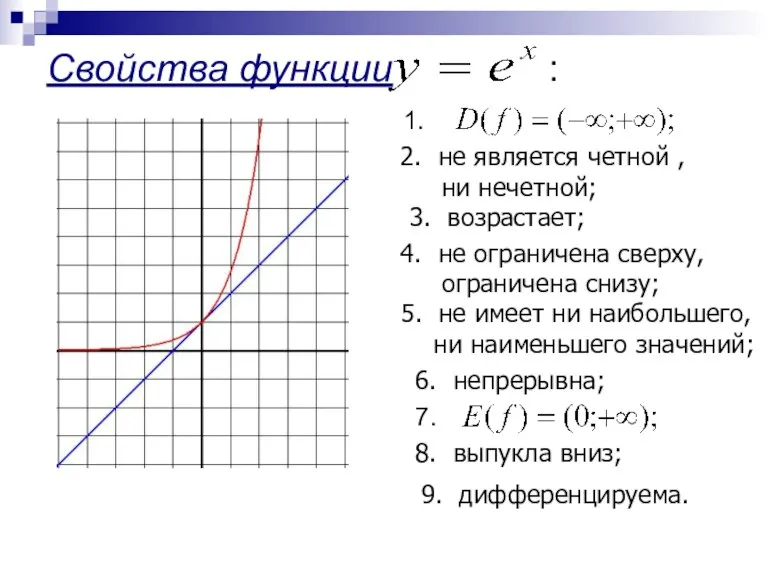
- 4. Свойства функции : 1. не является четной , ни нечетной; 3. возрастает; не ограничена сверху, ограничена
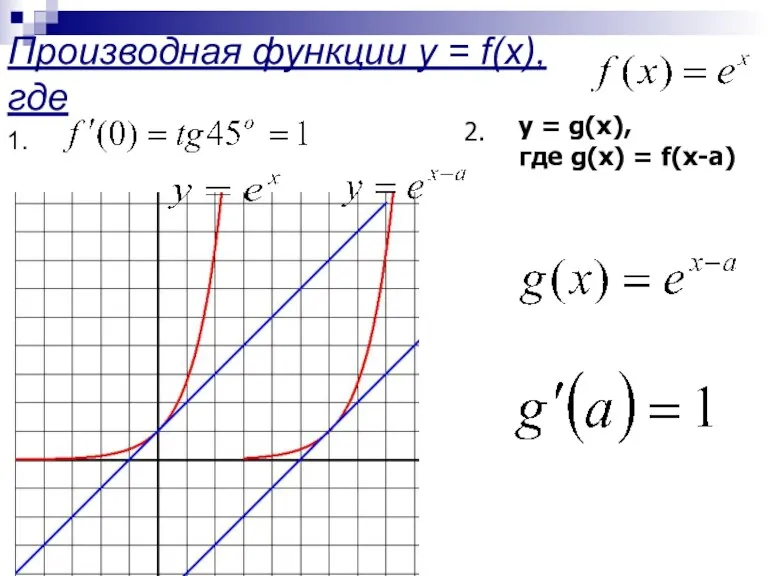
- 5. Производная функции y = f(x), где y = g(x), где g(x) = f(x-a) 2.
- 7. Пример 1. Провести касательную к графику функции в точке x=1. Решение: 1) a=1 2) f(a)=f(1)=e 3)
- 8. Пример 2. Вычислить значение производной функции в точке x=3. Решение: Ответ: 4
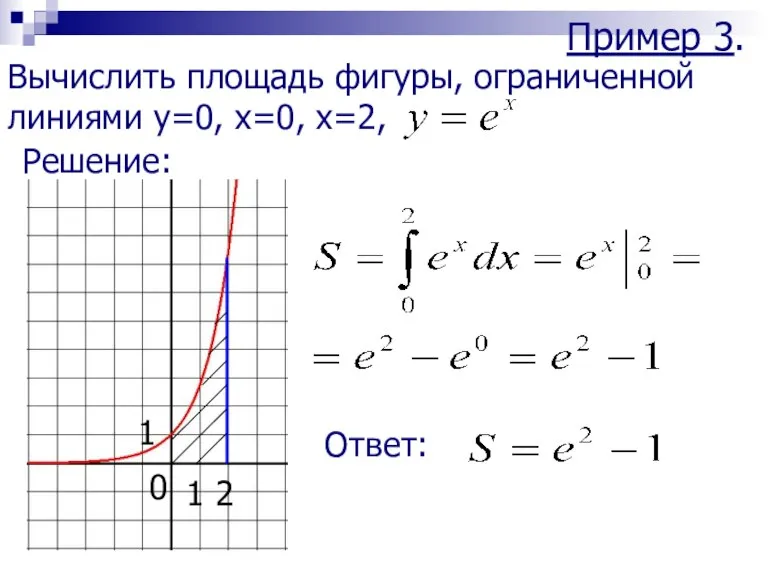
- 9. Пример 3. Вычислить площадь фигуры, ограниченной линиями y=0, x=0, x=2, Решение: 2 1 1 0 Ответ:
- 10. Пример 4. Исследовать на экстремум и схематически изобразить график функции Решение: 1) 2)
- 11. 3) -2 x 0 + + - 4) x=-2 – точка максимума x=0 – точка минимума
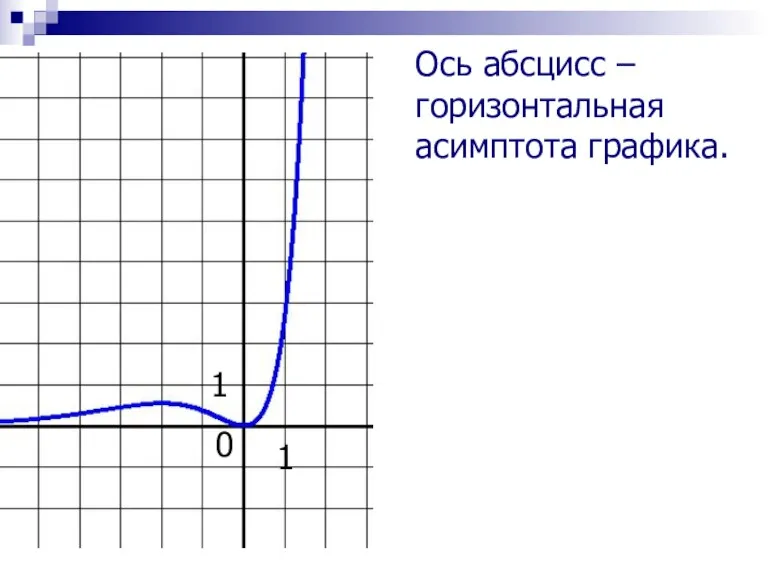
- 12. Ось абсцисс – горизонтальная асимптота графика. 0 1 1
- 13. Решите упражнения: 1620, 1623(a,б), 1624(а,б), 1628(а,б), 1629(а,б) Решить дома: 1621, 1623(в,г), 1624(в,г), 1628(в,г), 1629(в,г), 1631.
- 14. Натуральные логарифмы:
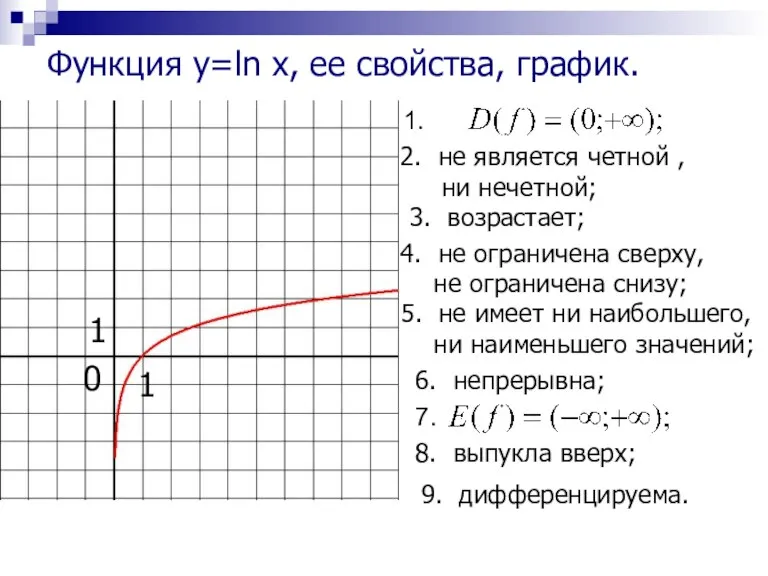
- 15. 1. не является четной , ни нечетной; 3. возрастает; не ограничена сверху, не ограничена снизу; не
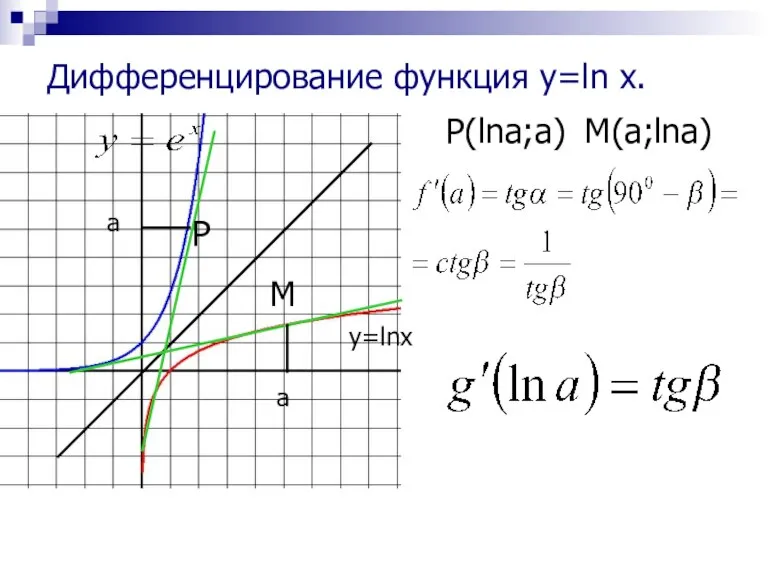
- 16. Дифференцирование функция y=ln x. y=lnx a a P(lna;a) P M M(a;lna)
- 19. Дифференцирование функции Например,
- 21. Скачать презентацию
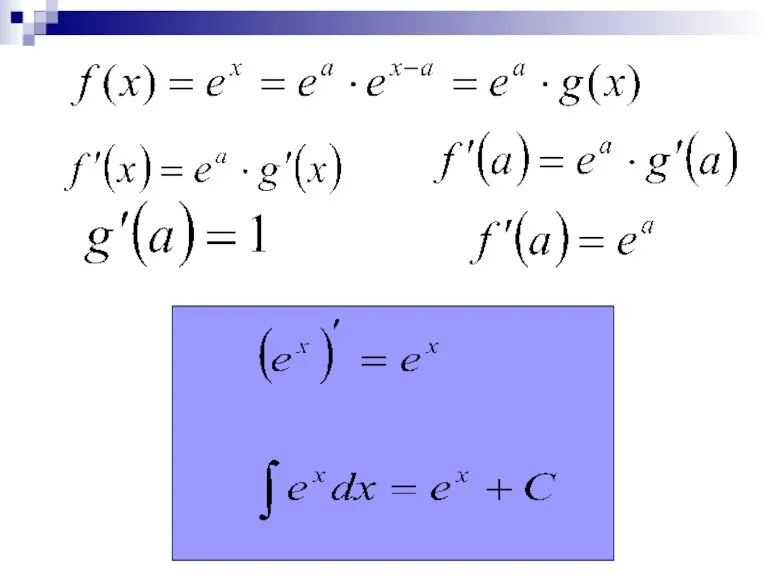






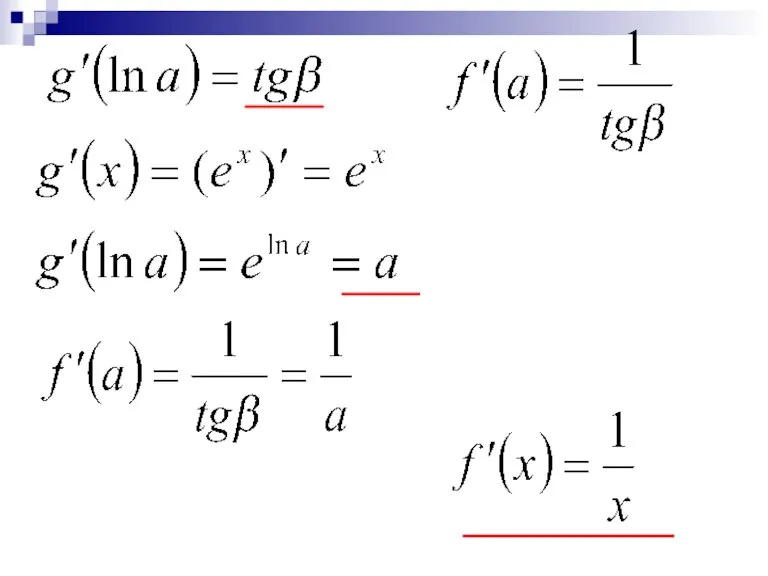
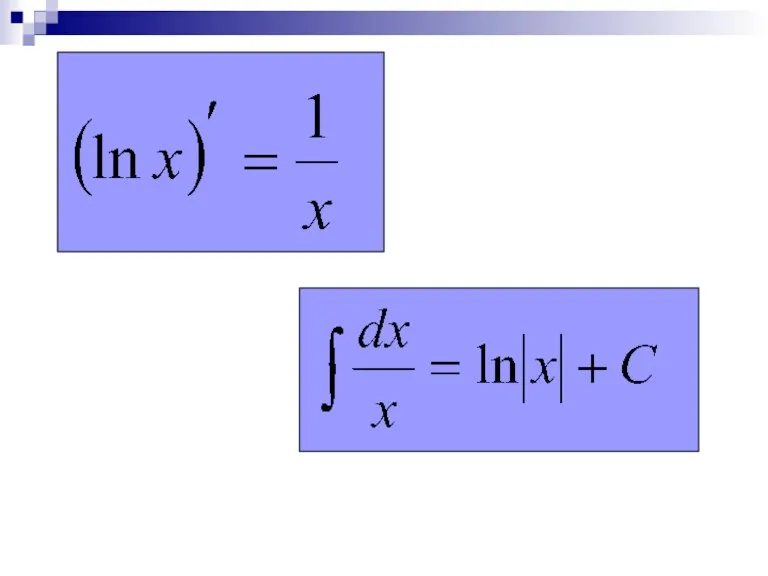

 Презентация на тему Состояние правового регулирования экологических прав граждан и общественных организаций по российскому зако
Презентация на тему Состояние правового регулирования экологических прав граждан и общественных организаций по российскому зако Тригонометрические уравнения Автор: Серебрянская Л. А.
Тригонометрические уравнения Автор: Серебрянская Л. А. ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Идентификация исполнителя неподлинной подписи
ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Идентификация исполнителя неподлинной подписи Квадратный трехчлен и его приложения
Квадратный трехчлен и его приложения Алгебраическая дробь. Сокращение дробей
Алгебраическая дробь. Сокращение дробей Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Обыкновенные дроби 5 класс
Обыкновенные дроби 5 класс Вычисление площадей плоских фигур - презентация по Алгебре_
Вычисление площадей плоских фигур - презентация по Алгебре_ Решение уравнений и неравенств, содержащих модуль, методом интервалов
Решение уравнений и неравенств, содержащих модуль, методом интервалов Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Квадратное уравнение Ладанова И.В. МКОУ «Верх-Жилинская ООШ»
Квадратное уравнение Ладанова И.В. МКОУ «Верх-Жилинская ООШ»  Презентация на тему НАУКА КАК СОЦИАЛЬНЫЙ ИНСТИТУТ
Презентация на тему НАУКА КАК СОЦИАЛЬНЫЙ ИНСТИТУТ  Арифметическая прогрессия
Арифметическая прогрессия Квадратные уравнения 8 класс
Квадратные уравнения 8 класс Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Умножение одночленов 7 класс
Умножение одночленов 7 класс Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов
Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов  Умножение натуральных чисел и его свойства
Умножение натуральных чисел и его свойства Презентация на тему Концепции TQC и CWQC
Презентация на тему Концепции TQC и CWQC  Классная работа. Пропорции. 11.01.13
Классная работа. Пропорции. 11.01.13 Решение систем линейных уравнений с двумя неизвестными Диктант Алгебра 7 класс
Решение систем линейных уравнений с двумя неизвестными Диктант Алгебра 7 класс Презентация на тему Материальная ответственность
Презентация на тему Материальная ответственность  Понятие бесконечной интегральной суммы. Интеграл
Понятие бесконечной интегральной суммы. Интеграл Функция y=sinx. Свойства. Преобразование графиков
Функция y=sinx. Свойства. Преобразование графиков Презентация на тему Современное искусство
Презентация на тему Современное искусство Функция
Функция koren-n-oy-stepeni.pptx
koren-n-oy-stepeni.pptx Презентация на тему Требования к гос. служащим
Презентация на тему Требования к гос. служащим