Понятие производной

Сегодня у нас праздник!
Эпиграф:
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.
А.Поуп.
Сегодня у нас праздник!

Что такое высшая математика?
Когда она появилась?
Что такое производная?

Как это было…

Ответим на вопрос:
Что такое скорость?

Возможно, это было так…
Пусть точка движется вдоль прямой по закону S(t).
Тогда за промежуток времени t точка проходит расстояние S(t).
Пусть ∆t – малый промежуток времени. Путь, пройденный за время t+ ∆t, равен S(t+ ∆t ).
Тогда средняя скорость

Очевидно, если ∆t 0, то Vср. Vмгн.
Значит,

А в это время…
Лейбниц Готфрид Вильгельм, немецкий математик , физик, философ.
Лейбниц – прямая противоположность И.Ньютону

И еще:
Одновременно, но независимо друг от друга они подошли к открытию анализа бесконечно малых.

Возможно, это было так…
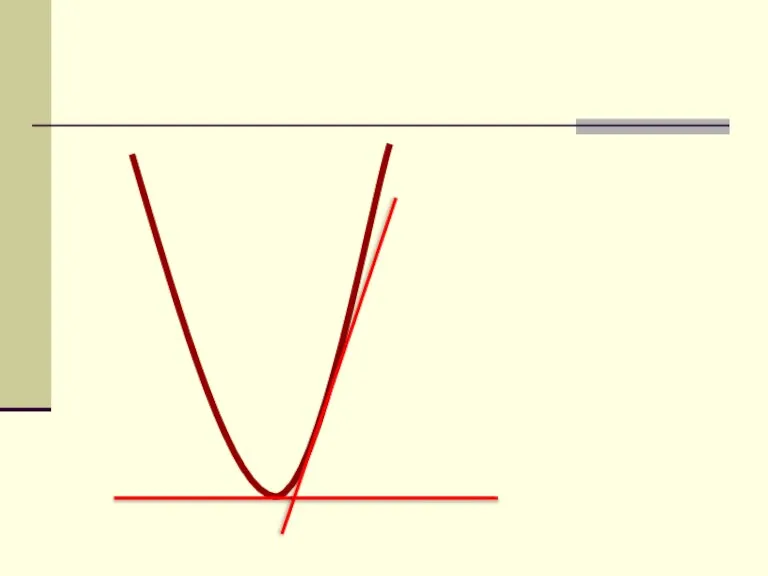
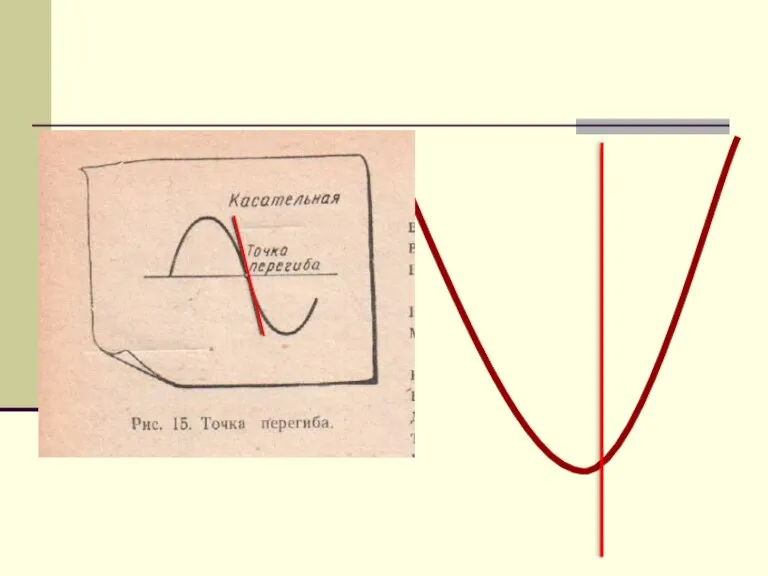
Началось все с касательной!!!

А что такое касательная?

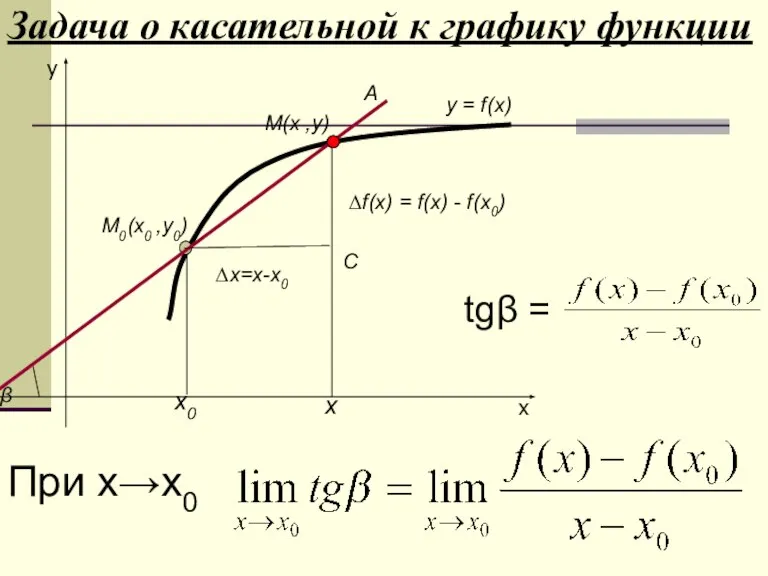
Задача о касательной к графику функции
x
y
С
∆х=х-х0
∆f(x) = f(x) - f(x0)

y
С
∆х=х-х0
∆f(x) = f(x) - f(x0)
Предельное положение секущей при
∆х 0
и называется касательной.
Причем,
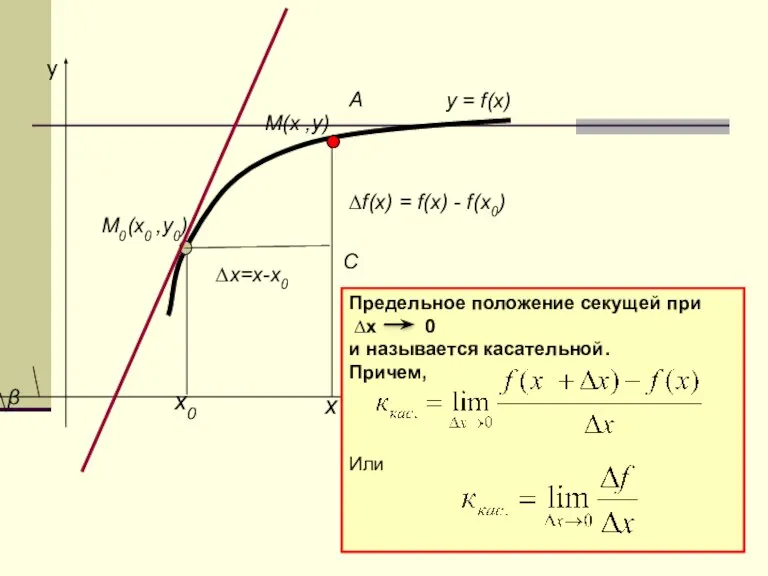
Или

Сравните:
По секрету:
это и есть производная!

Определение:
Производной функции y= f(x), заданной на интервале (a, b), в точке х этого интервала называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Итак,
Ньютон, а затем Лейбниц, независимо друг от друга, пришли к открытию дифференциального и интегрального исчислений.

Механический смысл производной:
Производная пути по времени есть скорость
V(t) = S’(t)