Возрастание и убывание функций

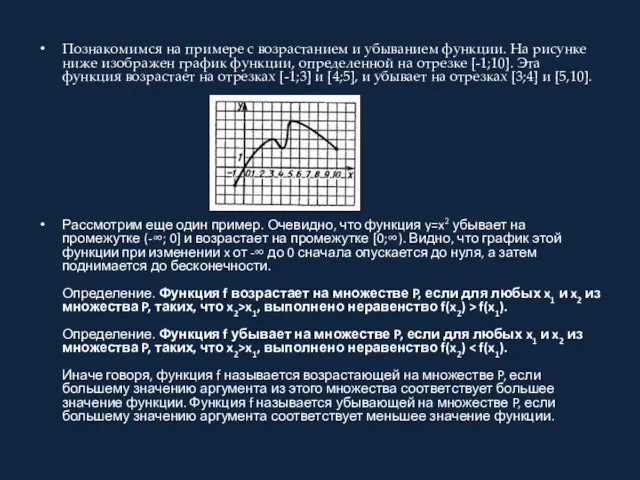
Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].
Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении x от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности.
Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1).
Определение. Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1).
Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.

Возрастание и убывание четных функций
Для четных функций задача нахождения промежутков возрастания и убывания сильно упрощается. Достаточно всего лишь найти промежутки возрастания и убывания при x≥0 (см. рисунок внизу).
Пусть, например, функция f четна и возрастает на промежутке [a;b], где b>a≥0. Докажем, что эта функция убывает на промежутке [-b; -a].
Действительно, пусть -a≥x2>x1≥-b. Тогда f(-x2)=f(x2), f(-x1)=f(x1), причем a≤-x2<-x1≤b, и, поскольку f возрастает на [a;b], имеем f(-x1)>f(-x2), то есть f(x1)>f(x2).

Возрастание и убывание функции синус
Докажем, что синус возрастает на промеждутках [-π/2+2πn ; π/2+2πn], n - целое. В силу периодичности функции синуса доказательство достаточно провести для отрезка [-π/2 ; π/2]. Пусть x2 > x1. Применим формулу разности синусов и найдем:
Из неравенства -π/2 ≤ x1 < x2 ≤ π/2 следует, что и , поэтому и , следовательно и .
Это доказывает, что на указанных промежутках синус возрастает.
Аналогичным образом легко доказать, что промежутки [π/2+2πn ; 3π/2+2πn], n - целое, являются промежутками убывания функции синуса.
Полученный результат можно легко проиллюстрировать с помощью рисунка единичной окружности (см. рисунок ниже). Если -π/2 ≤ t1 < t2 ≤ π/2, то точка Pt2 имеет ординату большую, чем точка Pt1. Если же π/2 ≤ t1 < t2 ≤ 3π/2, то ордината точки Pt2 меньше, чем ордината точки Pt1.

Возрастание и убывание функции косинус
Промежутками возрастания косинуса являются отрезки [-π+2πn ; 2πn], n - целое. Промежутками убывания косинуса являются отрезки [2πn ; π + 2πn], n - целое. Доказательство этих утверждений можно провести аналогично доказательству для синуса.
Однако, проще воспользоваться формулой приведения cos(x) = sin(x + π/2), из которой сразу следует, что промежутками возрастания косинуса являются промежутки возрастания синуса, сдвинутые на π/2 влево. Аналогичное утверждение можно сделать и для промежутков убывания.