Содержание
- 2. Определение квадратичной функции Функцию вида y = ax2 + bx + c, где a, b, c
- 3. График квадратичной функции Построить график функции y = x2 + 8x +7. Выделим полный квадрат, преобразовав
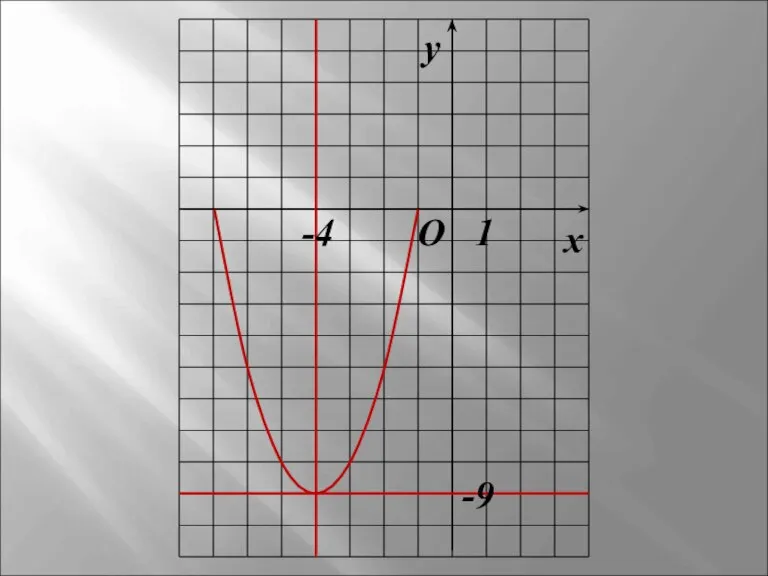
- 4. O x y 1 -9 -4
- 5. Построить график функции y = x2 + 3x +2. y = x2 + 2∙1,5∙x + 1,52
- 6. Алгоритм построения параболы Найти координаты вершины параболы А(хв, ув) по формулам построить эту точку в координатной
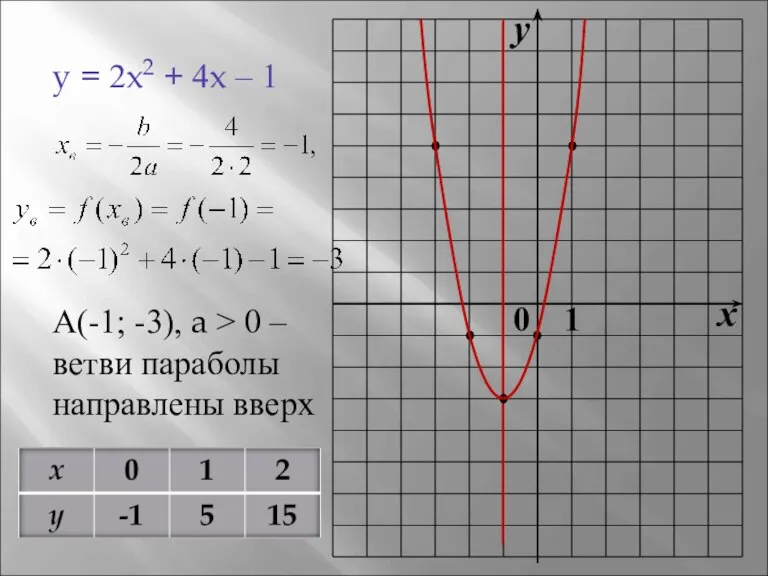
- 7. y = 2x2 + 4x – 1 А(-1; -3), a > 0 – ветви параболы направлены
- 8. Ответьте на вопросы Куда направлены ветви параболы? Найдите координаты вершины параболы. Запишите уравнение прямой, которая является
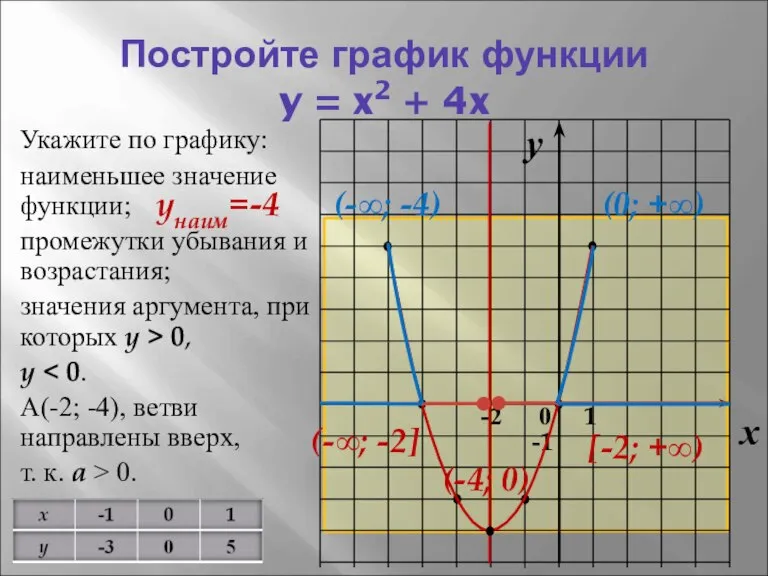
- 9. Постройте график функции y = x2 + 4x Укажите по графику: наименьшее значение функции; промежутки убывания
- 11. Скачать презентацию





 ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Идентификация исполнителя неподлинной подписи
ИССЛЕДОВАНИЕ ПОДПИСЕЙ, ВЫПОЛНЕННЫХ ПОД ВЛИЯНИЕМ СБИВАЮЩИХ ФАКТОРОВ Идентификация исполнителя неподлинной подписи Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей
Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей Презентация на тему Становление современной естественнонаучной картины мира
Презентация на тему Становление современной естественнонаучной картины мира  Уравнения с параметрами
Уравнения с параметрами Презентация на тему Основные философские школы Древнего Китая
Презентация на тему Основные философские школы Древнего Китая  Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости Презентация на тему Проблема интернализма и экстернализма в понимании механизмов научной деятельности
Презентация на тему Проблема интернализма и экстернализма в понимании механизмов научной деятельности  Тема: «Одночлены»
Тема: «Одночлены» Экскурсия в историю математики
Экскурсия в историю математики Производная функции
Производная функции Квадратичная функция
Квадратичная функция  Ряды Фурье
Ряды Фурье Презентация на тему Монизм, дуализм плюрализм в трактовке Бытия
Презентация на тему Монизм, дуализм плюрализм в трактовке Бытия Свойства числовых неравенств
Свойства числовых неравенств Статистические характеристики
Статистические характеристики Решение показательных уравнений
Решение показательных уравнений Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств Интегралы 11 класс
Интегралы 11 класс Zadachi-na-smesi-i-splavy.ppt
Zadachi-na-smesi-i-splavy.ppt Формула корней квадратного уравнения
Формула корней квадратного уравнения Арифметическая прогрессия
Арифметическая прогрессия Неопределённый интеграл и методы его исчисления
Неопределённый интеграл и методы его исчисления Презентация на тему Проблема научного метода в естествознании
Презентация на тему Проблема научного метода в естествознании  Презентация на тему Синтетические смолы и пластмассы
Презентация на тему Синтетические смолы и пластмассы  Построение графика линейной функции вида у= kx + b
Построение графика линейной функции вида у= kx + b Презентация на тему Особенности экспоненциального развития науки
Презентация на тему Особенности экспоненциального развития науки Комбинаторика Размещение и сочитание
Комбинаторика Размещение и сочитание Дифуры 1го порядка
Дифуры 1го порядка