Содержание
- 2. Квадратное уравнение имеет действительные положительные корни, если
- 3. Квадратное уравнение имеет действительные отрицательные корни, если
- 4. Квадратное уравнение имеет действительные корни различных знаков, причем положительный корень имеет больший модуль, если
- 5. Квадратное уравнение имеет действительные корни различных знаков, причем отрицательный корень имеет больший модуль, если
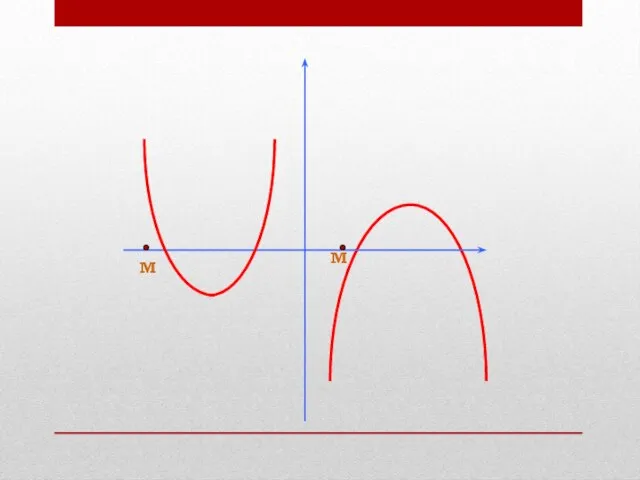
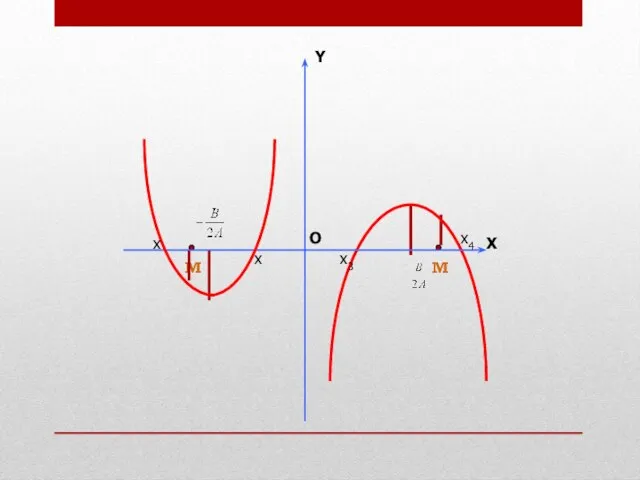
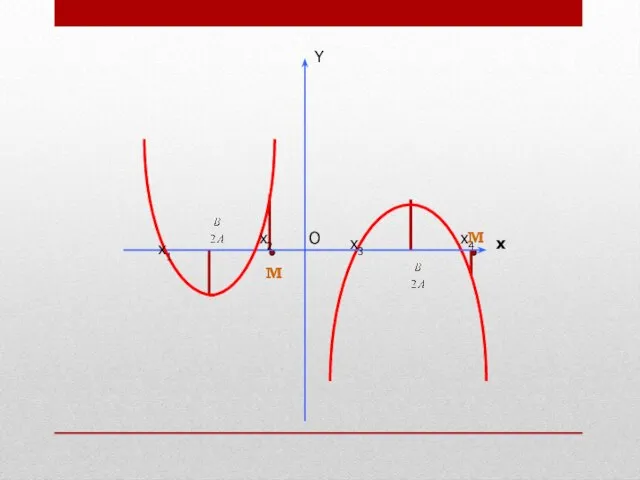
- 6. Расположение корней относительно заданной точки определяется направлением ветвей соответствующей параболы, координатами вершины и значениями в заданных
- 7. М М
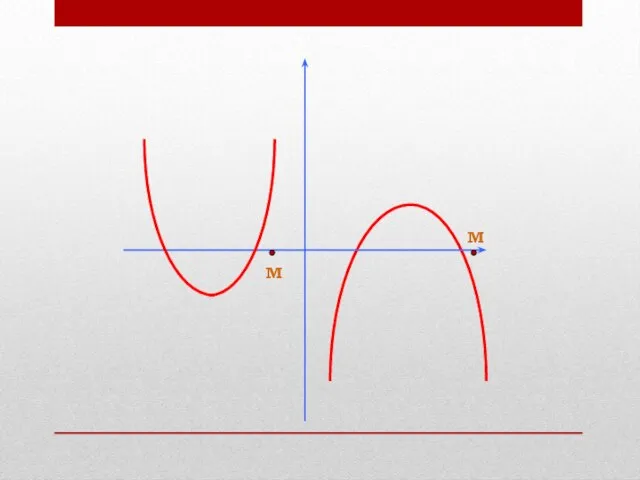
- 8. М М
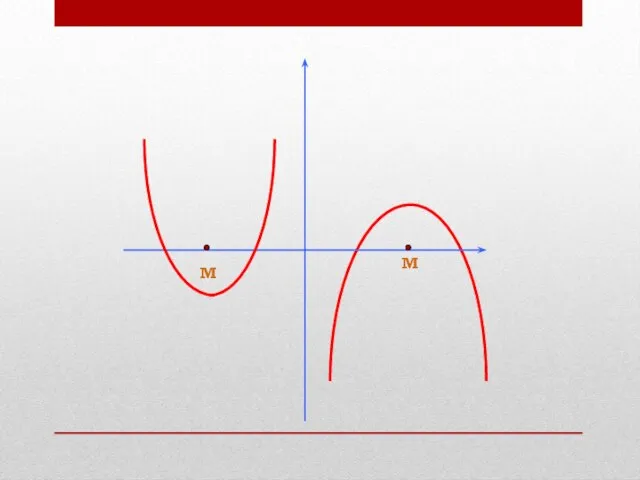
- 9. М М
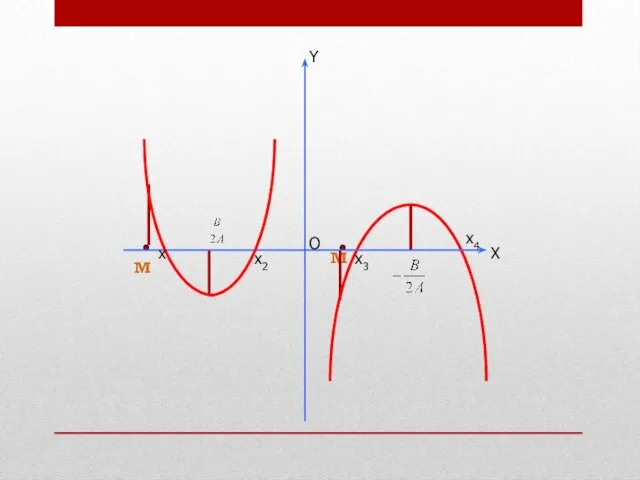
- 10. Оба корня квадратного трехчлена меньше числа М, тогда и только тогда, когда или
- 11. Оба корня квадратного трехчлена больше числа М, тогда и только тогда, когда или
- 12. Один из корней квадратного трехчлена меньше числа М, а другой больше числа М, тогда и только
- 13. При каких значениях параметра m уравнение имеет не более одного действительного корня?
- 14. При каких значениях параметра m корни уравнения различны и положительны?
- 15. При каких значениях параметра а корни уравнения таковы, что сумма их квадратов равна 1,75?
- 16. Нахождение значений параметра, при которых решения удовлетворяют некоторому условию.
- 17. Решение уравнений для всех значений параметра а
- 18. М М
- 19. М М
- 20. М М
- 22. При каких значениях параметра а корни квадратного уравнения х2 + (а + 1)х + 3 =
- 23. При каких значениях параметра а оба корня квадратного уравнения (2–a)x2-3ax+2a=0 больше ½. Решение. Рассмотрим функцию f(x)=
- 24. Найти все значения параметра а, при которых оба корня квадратного уравнения x2- 6ax+(2-2a+9a2)=0 больше 3. Решение.
- 26. Скачать презентацию

















 Алгебраические дроби
Алгебраические дроби  Презентация на тему ТК РФ как источник трудового права РФ
Презентация на тему ТК РФ как источник трудового права РФ  Презентация на тему Международные аукционы
Презентация на тему Международные аукционы  Урок по алгебре в 8 классе по теме: «Решение систем неравенств» . Учитель математики
Урок по алгебре в 8 классе по теме: «Решение систем неравенств» . Учитель математики  Teoriya-veroyatnostey-v-EGE.pptx
Teoriya-veroyatnostey-v-EGE.pptx Графики степенных функций
Графики степенных функций Свойства корня n-ой степени
Свойства корня n-ой степени Ещё раз о квадратных уравнениях
Ещё раз о квадратных уравнениях Неопределенный интеграл
Неопределенный интеграл Презентация на тему Виды коллизионных норм
Презентация на тему Виды коллизионных норм  Аналитические методы решения логарифмических уравнений
Аналитические методы решения логарифмических уравнений Квадратный корень
Квадратный корень Модуль числа 8 класс
Модуль числа 8 класс Графическое решение систем уравнений
Графическое решение систем уравнений Логарифмы
Логарифмы Квадратичная функция
Квадратичная функция  Квадратичная функция. Её свойства и график 8 класс
Квадратичная функция. Её свойства и график 8 класс Логарифмы
Логарифмы Удивительные квадратные уравнения
Удивительные квадратные уравнения Основные понятия, связанные с квадратными уравнениями
Основные понятия, связанные с квадратными уравнениями Понятие логарифма Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас
Понятие логарифма Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас  Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Квадратный корень из произведения
Квадратный корень из произведения Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к
Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к Полиномы Одночлены Двучлены Трёхчлены Многочлены
Полиномы Одночлены Двучлены Трёхчлены Многочлены  ГИА – 2013 г.Модуль «Алгебра». № 6
ГИА – 2013 г.Модуль «Алгебра». № 6 Методы решения систем уравнений МОУ - СОШ №6 Учитель математики Миссюра Ирина Николаевна
Методы решения систем уравнений МОУ - СОШ №6 Учитель математики Миссюра Ирина Николаевна  Базовые принципы системы smart-образования
Базовые принципы системы smart-образования