Содержание
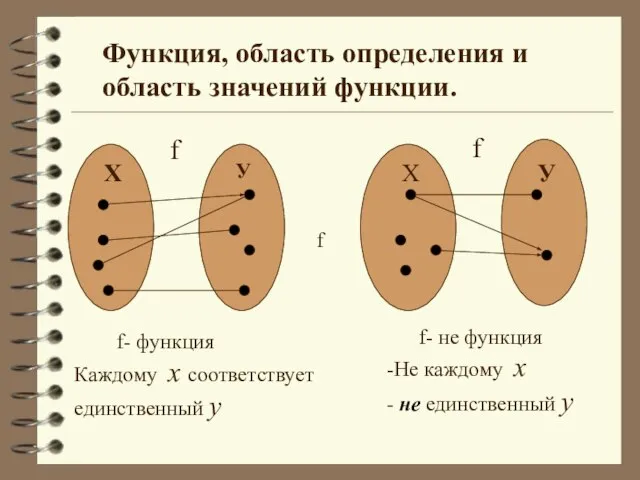
- 2. Функция, область определения и область значений функции. Х Х У У f f f- функция Каждому
- 3. Функцией (функциональной зависимостью) называется зависимость переменной у от переменной х, при которой каждому значению х соответствует
- 4. Все значения, которые может принимать аргумент (независимая переменная) образуют область определения функции. D (f) Все значения,
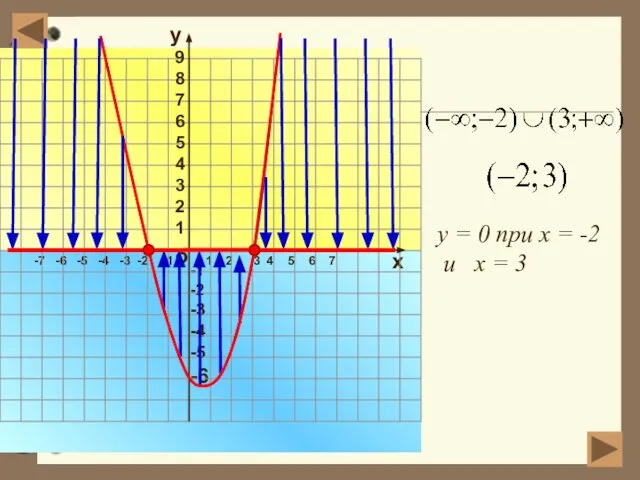
- 5. Свойства функции Значения аргумента, при которых функция обращается в нуль, называются нулями функции Промежутки, в которых
- 6. -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 о х
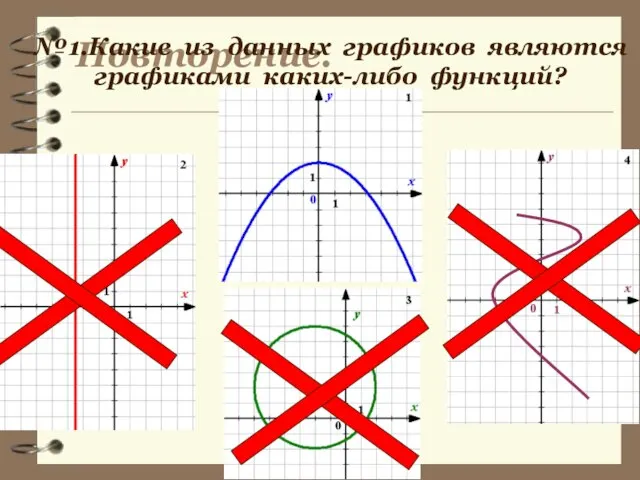
- 7. Повторение. №1.Какие из данных графиков являются графиками каких-либо функций?
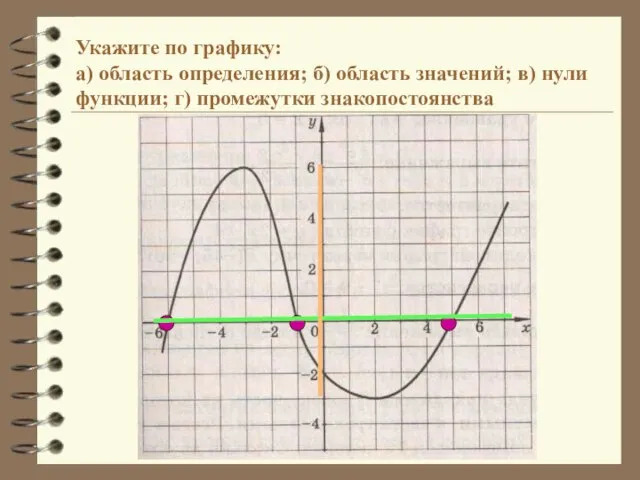
- 10. Укажите по графику: а) область определения; б) область значений; в) нули функции; г) промежутки знакопостоянства
- 11. у=f(x) – данная функция (уравнение с двумя переменными) Пара (х0;f(х0)) – решение уравнения и одновременно точка
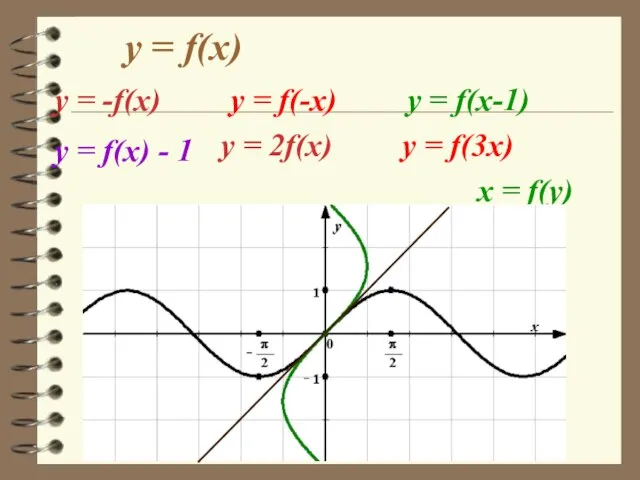
- 12. y = f(x) у = -f(x) y = f(-x) y = f(x-1) у = f(x) -
- 13. Построение графика функции с помощью геометрических преобразований Растяжение и сжатие
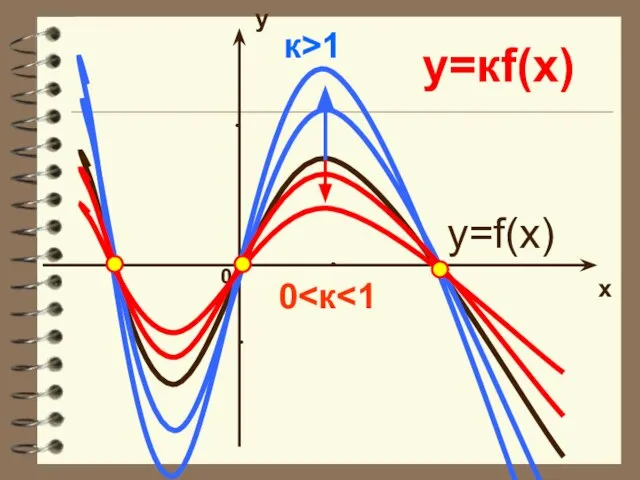
- 14. y x 0 y=кf(x) y=f(x) к>1 0
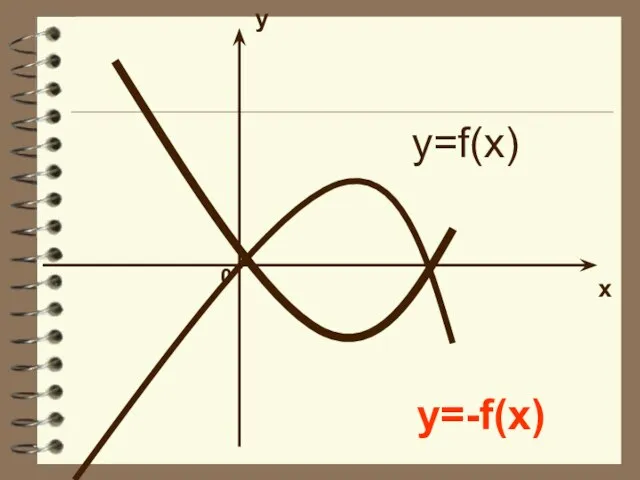
- 15. y x 0 y=f(x) y=-f(x)
- 16. для построения графика у = -к f(х) Сначала сжатие или растяжение Затем симметрия
- 17. Параллельный перенос графика При одинаковых значениях х , у отличаются на одно и тоже число. График
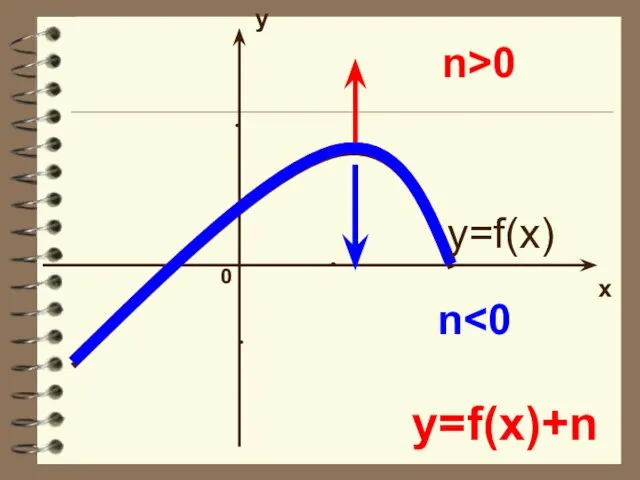
- 18. y x 0 y=f(x)+n n n>0 y=f(x)
- 19. Параллельный перенос графика При одинаковых значениях у , х отличаются на одно и тоже число. График
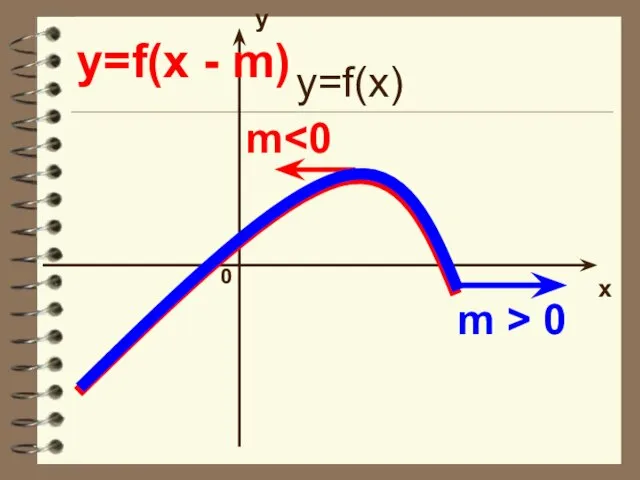
- 20. y x 0 y=f(x - m) m > 0 m y=f(x)
- 22. Скачать презентацию










 Дробно-рациональные уравнения
Дробно-рациональные уравнения Обыкновенныеи дроби (обобщение темы)
Обыкновенныеи дроби (обобщение темы) Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Статистические характеристики
Статистические характеристики Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Презентация на тему Движение Земли вокруг Солнца 2 класс
Презентация на тему Движение Земли вокруг Солнца 2 класс  Преобразования графиков функций 10 класс
Преобразования графиков функций 10 класс Крестовые походы
Крестовые походы Toplivno-energeticheskii_774_komplex_Rossii_9_klass_Prezentatsia_k_otkrytomu_uroku.pptx
Toplivno-energeticheskii_774_komplex_Rossii_9_klass_Prezentatsia_k_otkrytomu_uroku.pptx Уравнение касательной к графику функции в точке
Уравнение касательной к графику функции в точке Арифметическая прогрессия
Арифметическая прогрессия Квадратные уравнения
Квадратные уравнения Квадратные корни Алгебра 8 класс
Квадратные корни Алгебра 8 класс  Презентация на тему Рынок недвижимости
Презентация на тему Рынок недвижимости  Презентация на тему Хрусталь
Презентация на тему Хрусталь Презентация на тему Виды и особенности экологических правоотношений
Презентация на тему Виды и особенности экологических правоотношений Франсуа Виет 1540 - 1603
Франсуа Виет 1540 - 1603 Обобщающий урок по теме: «Решение неравенств с одной переменной и решение систем неравенств»
Обобщающий урок по теме: «Решение неравенств с одной переменной и решение систем неравенств» Решение неравенств с одной переменной и решение систем неравенств
Решение неравенств с одной переменной и решение систем неравенств Одночлены и многочлены 7 класс
Одночлены и многочлены 7 класс Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Презентация на тему Современное искусство
Презентация на тему Современное искусство Презентация на тему Становление современной естественнонаучной картины мира
Презентация на тему Становление современной естественнонаучной картины мира  Первообразная
Первообразная Pervyy-urok-algebry.ppt
Pervyy-urok-algebry.ppt Линейная функция и ее график
Линейная функция и ее график Производная (11 класс)
Производная (11 класс) Тригонометрические неравенства
Тригонометрические неравенства