Содержание
- 2. Изучить правила преобразования рациональных выражений; Научиться упрощать выражения; Научиться доказывать тождества. Цели: 26.06.2011 Кравченко Г. М.
- 3. 26.06.2011 Кравченко Г. М. Рациональные числа - все целые числа и все дроби, как положительные так
- 4. 26.06.2011 Кравченко Г. М. Для преобразования рациональных выражений принят тот же порядок действий, что и для
- 5. 26.06.2011 Кравченко Г. М. Рассмотрим пример 1. Упростить выражение. 1 1 1 1
- 6. 26.06.2011 Кравченко Г. М. Решение Рассмотрим пример 2. Упростить выражение: Для упрощения выражения выбираем способ преобразования
- 7. 26.06.2011 Кравченко Г. М. 1 1 1 1
- 8. 26.06.2011 Кравченко Г. М. Рассмотрим пример 3. Упростить выражение:
- 9. 26.06.2011 Кравченко Г. М.
- 10. 26.06.2011 Кравченко Г. М. 1 1 1 1 1 1
- 11. 26.06.2011 Кравченко Г. М. Доказать тождество – это значит установить, что при всех допустимых значениях переменной
- 12. 26.06.2011 Кравченко Г. М. Рассмотрим пример 4. Доказать тождество. Для доказательства тождества выбираем первый способ: преобразуем
- 13. 26.06.2011 Кравченко Г. М. 1 1 1 1 И так, 8 = 8. Тождество справедливо лишь
- 15. Скачать презентацию





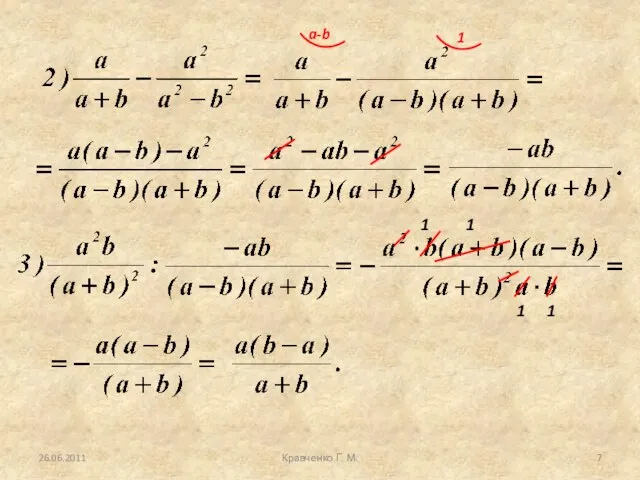

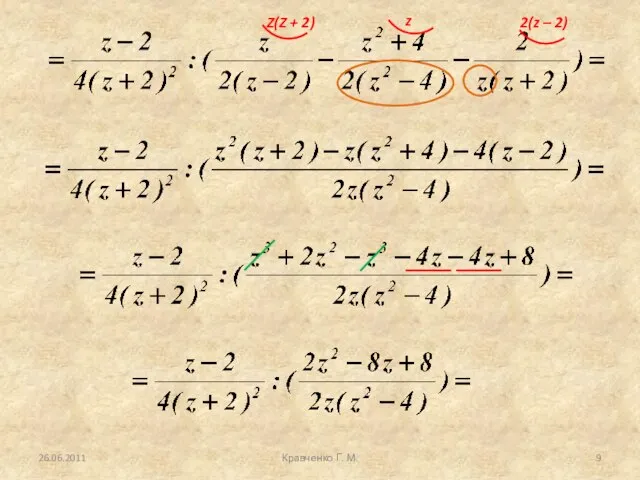
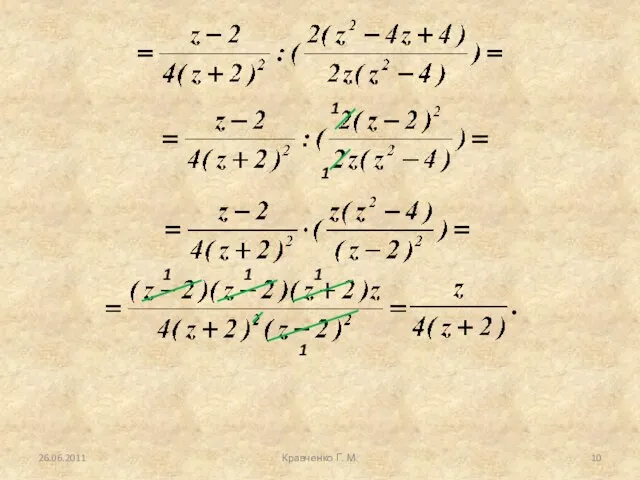



 Умножение натуральных чисел и его свойства
Умножение натуральных чисел и его свойства Квадратные уравнения и уравнения, приводимые к квадратным - презентация по Алгебре_
Квадратные уравнения и уравнения, приводимые к квадратным - презентация по Алгебре_ Системы уравнений
Системы уравнений Уравнение прямой на плоскости
Уравнение прямой на плоскости Предел функции в точке
Предел функции в точке Презентация на тему Закономерности и особенности создания Древнерусского государства
Презентация на тему Закономерности и особенности создания Древнерусского государства  Интегралы
Интегралы Алгебра 8 класс Фадеева Светлана Виссарионовна МОУ Кожважская основная общеобразовательная школа
Алгебра 8 класс Фадеева Светлана Виссарионовна МОУ Кожважская основная общеобразовательная школа  Отношения и пропорции
Отношения и пропорции Квадратные уравнения 8 класс
Квадратные уравнения 8 класс mat
mat Неравенства с двумя переменными
Неравенства с двумя переменными Функции и графики
Функции и графики Математика 5 класс
Математика 5 класс Метод рационализации
Метод рационализации Презентация на тему Основные обязанности гражданского служащего, а также запреты и ограничения, связанные с гражданской службой
Презентация на тему Основные обязанности гражданского служащего, а также запреты и ограничения, связанные с гражданской службой  Функция y=ax2+bx+c, её свойства и график
Функция y=ax2+bx+c, её свойства и график Исследование функции на монотонность и экстремумы
Исследование функции на монотонность и экстремумы Тригонометрические уравнения и методы их решения
Тригонометрические уравнения и методы их решения Правила безопасности на воде
Правила безопасности на воде  Прогрессии 9 класс
Прогрессии 9 класс В лабиринте тригонометрических формул
В лабиринте тригонометрических формул Модуль числа 8 класс
Модуль числа 8 класс neravenstva-s-dvumya-peremennymi.ppt
neravenstva-s-dvumya-peremennymi.ppt Сложение и вычитание обыкновенных дробей с одинаковым знаменателем
Сложение и вычитание обыкновенных дробей с одинаковым знаменателем Последовательности
Последовательности Тригонометрические функции и их графики
Тригонометрические функции и их графики Уравнения, содержащие знак модуля
Уравнения, содержащие знак модуля