Линейное уравнение с двумя переменными и его график

Линейное уравнение с двумя переменными и его график
Цель: дать понятие об уравнении с двумя переменными, их решении и графике уравнения
*

Линейное уравнение с двумя переменными и его график
Повторение материала:
Алгоритм нахождения координат точки.
Алгоритм построения точки в системе координат.
Укажите координаты точек В и С, симметричных точке А(-5; 2) относительно оси х и оси у соответственно.
*

Линейное уравнение с двумя переменными и его график
Пример 1.
Первое число (обозначим его х) больше квадрата второго числа (обозначим его у) на 3.
х – у² = 4
Выполняется ли это равенство при х=20 и у = 4?
А при х = 15 и у = 2?
*

Линейное уравнение с двумя переменными и его график
х – у² = 4
Подобные равенства с двумя переменными называют уравнениями с двумя переменными. Пару чисел х = 20 и у = 4 называют решением уравнения.
Решение можно записать также в виде (20; 4).
*

Линейное уравнение с двумя переменными и его график
Равенство, содержащее две переменные, называется уравнением с двумя переменными.
Если в уравнении неизвестные входят только в первой степени, то такое уравнение называют линейным уравнением с двумя переменными.
Линейное уравнение имеет вид ах + bу + с=0 (где х и у – переменные, а, b, с – некоторые числа.
*

Линейное уравнение с двумя переменными и его график
Например, линейными являются уравнения
3х – 4у + 1 = 0, 5х + 7у = 0 и т. д.
Решением уравнения с двумя неизвестными называется пара значений переменных (х; у), при подстановке которых уравнение становится верным числовым равенством.
*

Линейное уравнение с двумя переменными и его график
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными.
Уравнения с двумя переменными, не имеющие решений, также считаю равносильными.
*

Линейное уравнение с двумя переменными и его график
Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной.
Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Если обе части уравнения умножить или разделить на одно и то же (не равное нулю), то получится уравнение, равносильное данному.
*

Линейное уравнение с двумя переменными и его график
Пример 2
а) Уравнения 3х² + 4у³ = 5 и 3х² = 5 – 4у³ равносильны, т.к. член 4у³ перенесён (с изменением знака) из левой части в правую.
б) Уравнения и 3х² + 4у³ = 5 равносильны, т.к. обе части первого уравнения умножили на число 12 (не равное нулю) и получили второе.
*

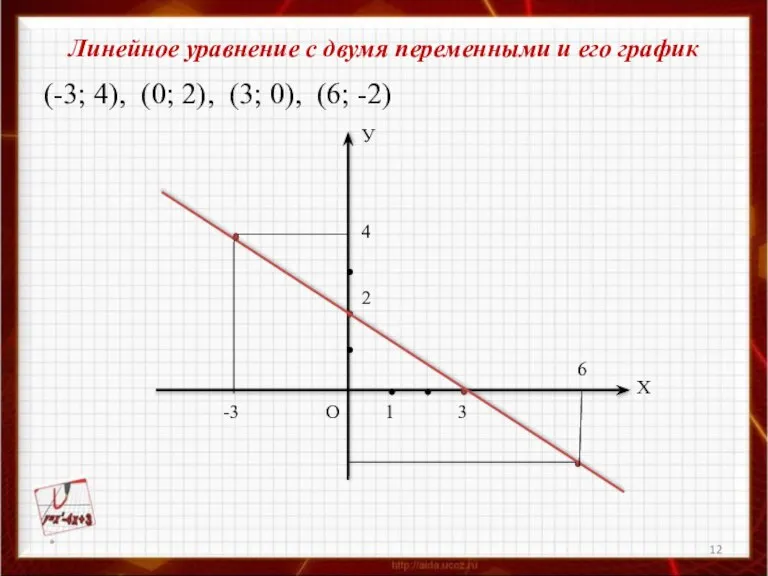
Линейное уравнение с двумя переменными и его график
Пример 3
Рассмотрим линейное уравнение 2х + 3у – 6 = 0 и построим его график.
Подберём несколько решений данного уравнения.
(-3; 4), (0; 2), (3; 0), (6; -2)
Построим эти точки на координатной плоскости.
*

Линейное уравнение с двумя переменными и его график
(-3; 4), (0; 2), (3; 0), (6; -2)
*
У
Х
6
2
4
О
1
-3
3

Линейное уравнение с двумя переменными и его график
Замечания по примеру
1 Для построения графика уравнения 2х + 3у – 6 = 0
можно было не подбирать, а находить такие
решения.
2х + 3у – 6 = 0
3у = – 2х + 6
*

Линейное уравнение с двумя переменными и его график
Замечания по примеру
2. Графиком линейного уравнения ах + bу + с = 0
является прямая линия.
3. Для построения прямой достаточно двух точек.
4. В качестве этих точек удобно выбирать точки пересечения графика функции с осями координат.
*

Линейное уравнение с двумя переменными и его график
Задание на уроке:
№ 7.1(а); 7.2(б); 7.4(г); 7.7(а); 7.11(б); 7.14(г); 7.17(а, г); 7.25(а); 7.28(б); 7.29(б); 7.30; 7.39(а, б);
*

Линейное уравнение с двумя переменными и его график
Домашнее задание:
№ 7.1(б); 7.2(а); 7.4(в); 7.7(б); 7.11(г); 7.14(б); 7.17(б, в); 7.25(б); 7.28(а); 7.29(а); 7.31; 7.39(в, г);
*