Содержание
- 2. Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача.
- 3. Дано: Найти: t – ? Решение: , т.е. Обратимая функция Обратная функция к v( t )
- 4. Если функция у = f ( х ) принимает каждое своё значение у только при одном
- 5. Дано: Найти функцию, обратную данной у = f -1(x). Решение: Ответ:
- 6. х х у у 0 0 2 2 D(у)=(-∞;2)∪(2;+∞) Е(у)=(-∞;0)∪(0;+∞) 2. Е(у)=(-∞;2)∪(2;+∞) D(у)=(-∞;0)∪(0;+∞)
- 7. Свойства обратных функций. Область определения обратной функции f -1 совпадает с множеством значений исходной f, а
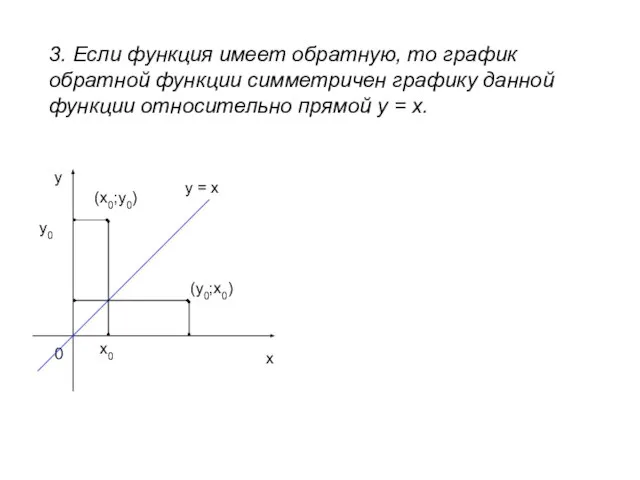
- 8. 3. Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у
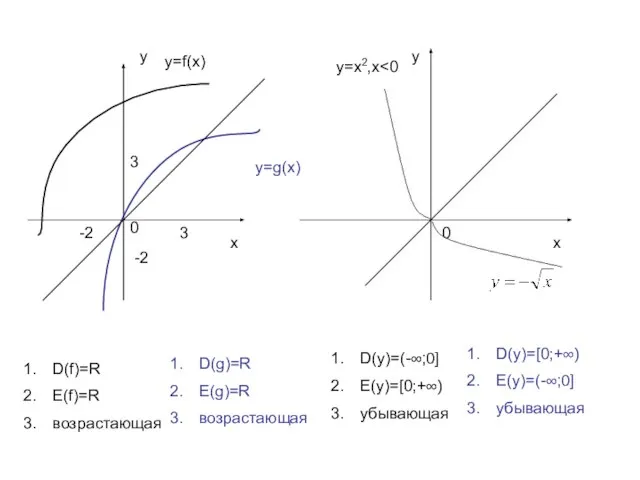
- 9. у х х у 0 0 3 3 -2 -2 у=f(x) у=g(x) y=x2,х D(f)=R E(f)=R возрастающая
- 11. Скачать презентацию




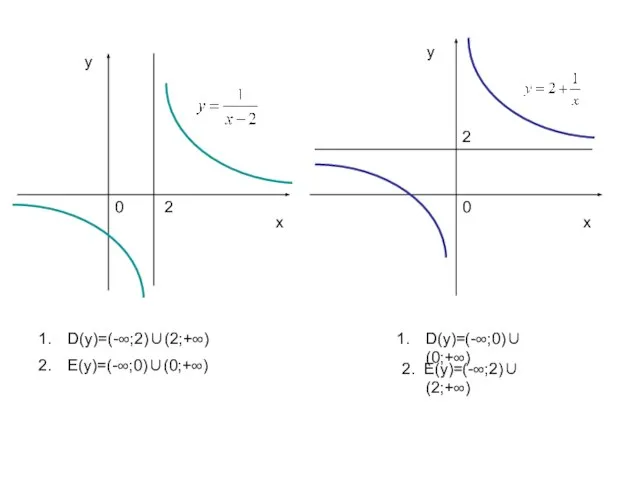

 Функция Презентация выполнена учителем математики МБОУ СОШ № 22 Т. П. Лисицыной, п. Пересыпь, Темрюкского района, Краснодарс
Функция Презентация выполнена учителем математики МБОУ СОШ № 22 Т. П. Лисицыной, п. Пересыпь, Темрюкского района, Краснодарс Применение производной к исследованию функций
Применение производной к исследованию функций Нестандартно мыслим
Нестандартно мыслим Интегралы
Интегралы Степень с целым показателем 8 класс
Степень с целым показателем 8 класс Решение дробных рациональных уравнений
Решение дробных рациональных уравнений Решение неравенств методом интервалов
Решение неравенств методом интервалов Умножение одночленов 7 класс
Умножение одночленов 7 класс Функция y = x^2
Функция y = x^2 Презентация на тему Организационная структура системы таможенных органов РФ
Презентация на тему Организационная структура системы таможенных органов РФ Последовательности
Последовательности Презентация по математике на тему: «Метод математической индукции»
Презентация по математике на тему: «Метод математической индукции»  Старая сказка на новый лад
Старая сказка на новый лад Таблицы истинности
Таблицы истинности математики и литература
математики и литература Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Презентация на тему Проблема интернализма и экстернализма в понимании механизмов научной деятельности
Презентация на тему Проблема интернализма и экстернализма в понимании механизмов научной деятельности  ГИА – 2013 г.Модуль «Алгебра». № 6
ГИА – 2013 г.Модуль «Алгебра». № 6 Натуральные логарифмы
Натуральные логарифмы Закрепление основных разделов из курса «Алгебра и начала анализа. 10 – 11 класс»
Закрепление основных разделов из курса «Алгебра и начала анализа. 10 – 11 класс» Неопределённый интеграл и методы его исчисления
Неопределённый интеграл и методы его исчисления Презентация на тему Система высшего образования в Японии
Презентация на тему Система высшего образования в Японии  «Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе
«Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе  zakony-algebry-logiki.pptx
zakony-algebry-logiki.pptx Алгебраические комедии софизмы - презентация по Алгебре
Алгебраические комедии софизмы - презентация по Алгебре МБОУ «чульская основная общеобразовательная школа» Учитель Генералова О.В. Определение степени с натуральным показателем 7
МБОУ «чульская основная общеобразовательная школа» Учитель Генералова О.В. Определение степени с натуральным показателем 7 ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков
ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков  Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей