Предел последовательности и функции

Цели:
Сформировать понятие предела последовательности, функции;
Ввести понятие сходящихся и расходящихся последовательностей, горизонтальной асимптоты;
Сформировать умения вычисления пределов.

Пояснительная записка
Изучение данного учебного элемента разбито
на несколько этапов. После каждого этапа вам
необходимо будет выполнить практические
задания в своей рабочей тетради.
По окончании изучения элемента вам
предстоит выполнить контрольную работу по
этой теме также в своей тетради. Рабочую
тетрадь по окончании изучения сдать
на проверку учителю.
Желаем удачи!

Сопутствующие учебные материалы
Алгебра и начала анализа. 10 -11 кл.: Учебник для общеобразоват. учреждений / А. Г. Мордкович. : 2-е – изд. – М.: Мнемозина, 2001;
Алгебра и начала анализа. 10 -11 кл.: Задачник для общеобразоват. Учреждений / А. Г. Мордкович, Л. О. Денисова, Т. Н. Мишустина, Е. Е. Тульчикова. - 2-е – изд. – М.: Мнемозина, 2001;
Рабочая тетрадь.

Опорные знания
Для успешного изучения данного
учебного элемента вы должны знать:
Что такое функция;
Что такое числовая последовательность;
Какими свойствами обладают числовые последовательности.

Предел числовой последовательности
Рассмотрим две числовые последовательности:
: 2, 4, 6, 8, 10, …, ,…;
: 1, , , , , … , …
Изобразим члены этих последовательностей
точками на координатных прямых.
Обратите внимание как ведут себя члены
последовательности.

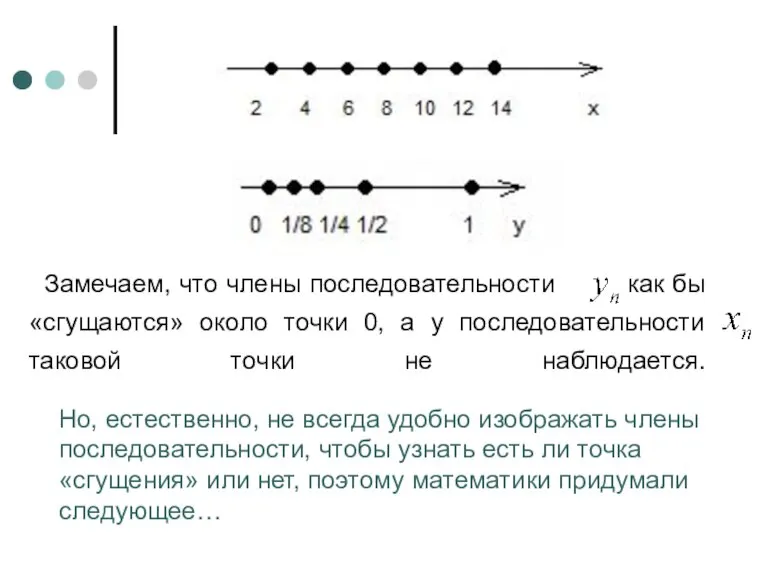
Замечаем, что члены последовательности как бы «сгущаются» около точки 0, а у последовательности таковой точки не наблюдается.
Но, естественно, не всегда удобно изображать члены последовательности, чтобы узнать есть ли точка «сгущения» или нет, поэтому математики придумали следующее…

Определение 1. Пусть a - точка прямой, а r -
положительное число. Интервал (a-r, a+r)
называют окрестностью точки a , а число r - радиусом окрестности.
Геометрически это выглядит так:

Теперь можно перейти к определению точки
«сгущения», которую математики назвали
«пределом последовательности».
Например
(-0.1, 0.5) – окрестность точки 0.2, радиус окрестности равен 0. 3.

Определение 2. Число
называют пределом
последовательности
, если в любой заранее
выбранной окрестности точки
содержатся
все члены последовательности, начиная с некоторого номера.
Пишут: .
Читают:
стремится к .
Либо пишут: .
Читают: предел последовательности при
стремлении к бесконечности равен .

Комментарий
Пусть . Возьмем окрестность точки r радиуса,
r, то есть (b-r, b+r) . Тогда существует такой номер n1 ,
начиная с которого все последующие члены
последовательности содержатся внутри указанной
окрестности, например, yn+1, yn+8 и т. д., а вне этой
окрестности содержится конечное числа членов
последовательности y1, yn-1, yn-5 и т. д.
При этом, если выбрать другую окрестность (другого
радиуса), то для нее также найдется какой – то номер, начиная с
которого все последующие члены последовательности будут
попадать в указанный интервал.

Пример.
Существует ли номер , начиная с которого все члены последовательности попадают в окрестность точки радиуса , если
1.
Решение.

Пример
Существует ли номер n0, начиная с которого все члены последовательности (хn) попадают в окрестность точки а радиуса r=0.1, если а=0, хn=
Решение
Ответ: начиная с n0=4 все члены последовательности (хn) попадают
в окрестность (-0.1;0.1)

Практические задания
1. Запишите окрестность точки радиуса в виде интервала, если:
2. Окрестностью какой точки и какого радиуса является интервал:
3. Принадлежит ли точка окрестности точки радиуса , если:

Содержание
Сходящиеся последовательности и их свойства, расходящиеся последовательности;
Вычисление пределов числовой последовательности;
Графический смысл предела;
Сумма бесконечной геометрической прогрессии;
Предел функции на бесконечности;
Предел функции в точке.
Итоговое задание

Итоговое практическое задание
1. Существует ли номер , начиная с которого все члены последовательности попадают в окрестность точки радиуса :
2. Постройте график последовательности
и составьте,
если это возможно, уравнение горизонтальной асимптоты графика: