Содержание
- 2. I. Математический диктант 1)D(y)= 2)E(y)= 3) 4)sin(-x)=-sin x 5)Возрастает на Убывает на 6)Периодичная I вариант y=sin
- 3. Функция y=sin x, график и свойства. 1)D(y)= 2)E(y)= 3) 4)sin(-x)=-sin x 5)Возрастает на Убывает на 6)Периодичная
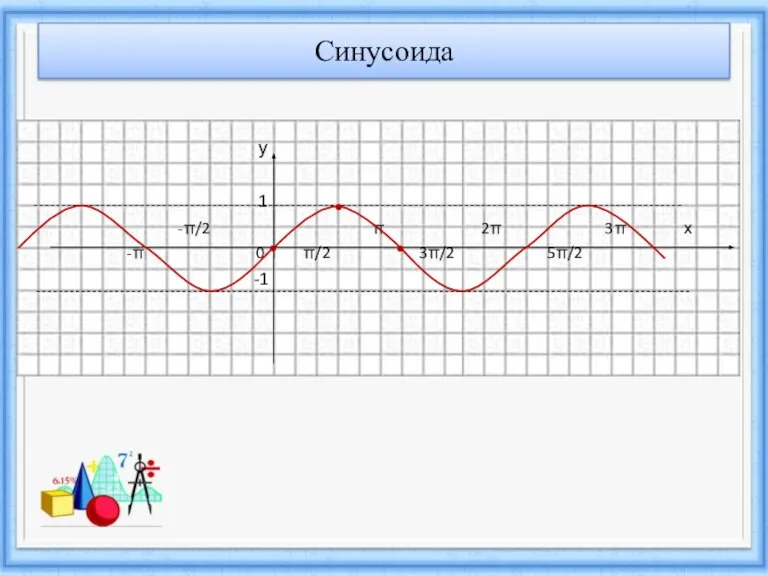
- 4. Синусоида у 1 -π/2 π 2π 3π х -π 0 π/2 3π/2 5π/2 -1
- 5. Функция y = cos x, её свойства и график. 1)D(y)= 2)E(y)= 3) 4)cos(-x)=cosx 5)Возрастает на Убывает
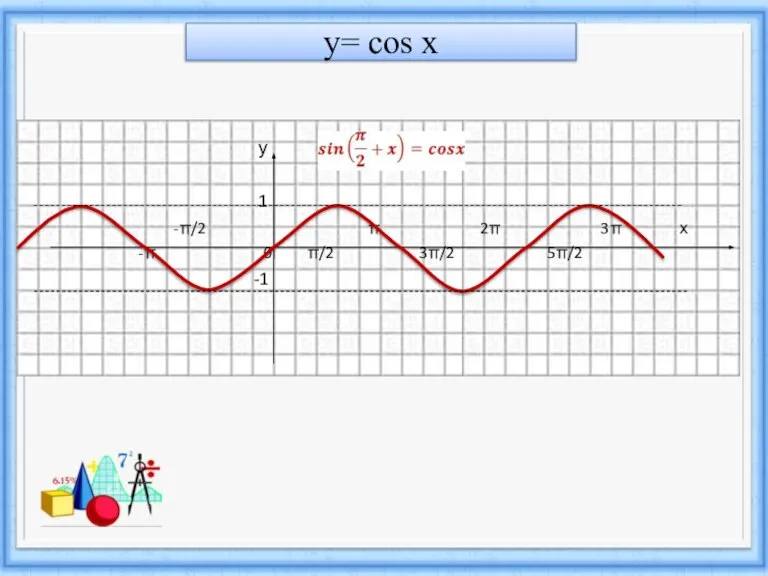
- 6. y= cos x у 1 -π/2 π 2π 3π х -π 0 π/2 3π/2 5π/2 -1
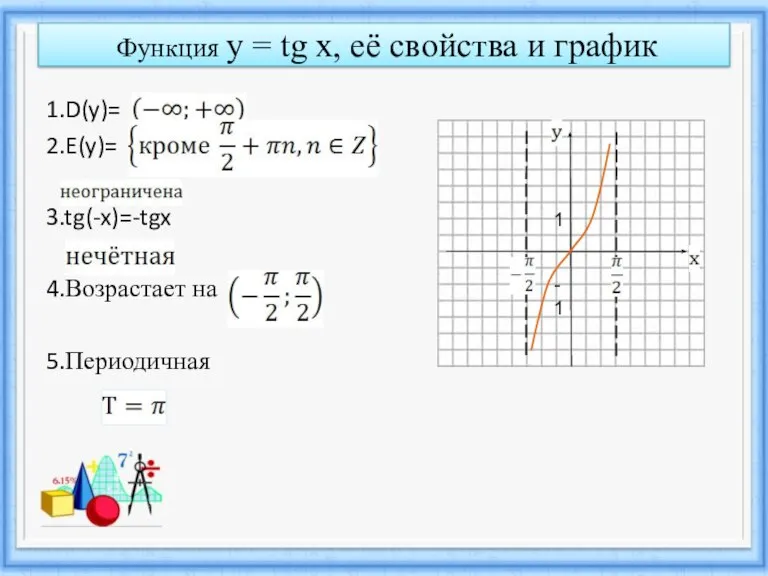
- 7. Функция y = tg x, её свойства и график 1.D(y)= 2.E(y)= 3.tg(-x)=-tgx 4.Возрастает на 5.Периодичная 1
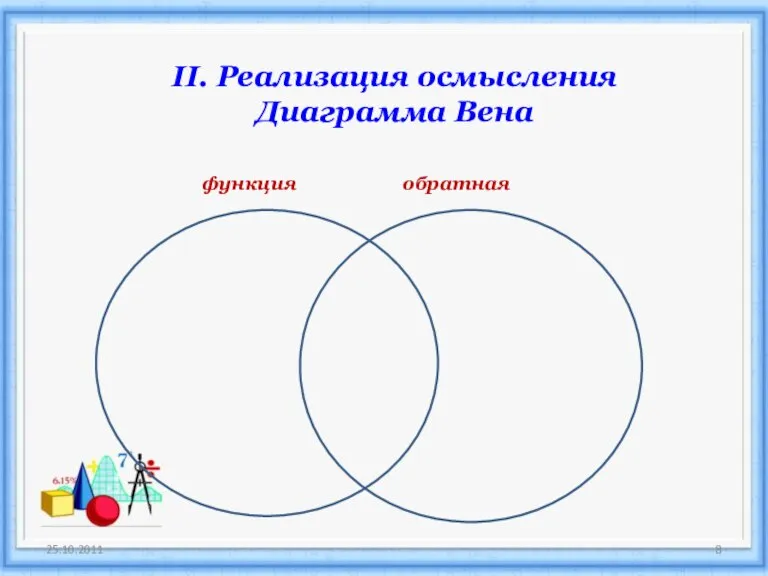
- 8. II. Реализация осмысления Диаграмма Вена функция обратная
- 9. III. Проблемная ситуация 1. Могут ли тригонометрические функции в своих областях определения иметь обратные себе функции?
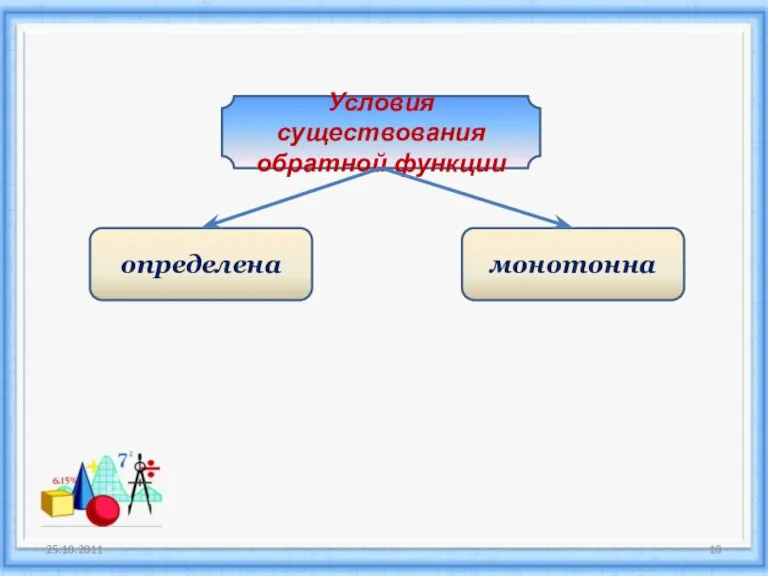
- 10. Условия существования обратной функции определена монотонна
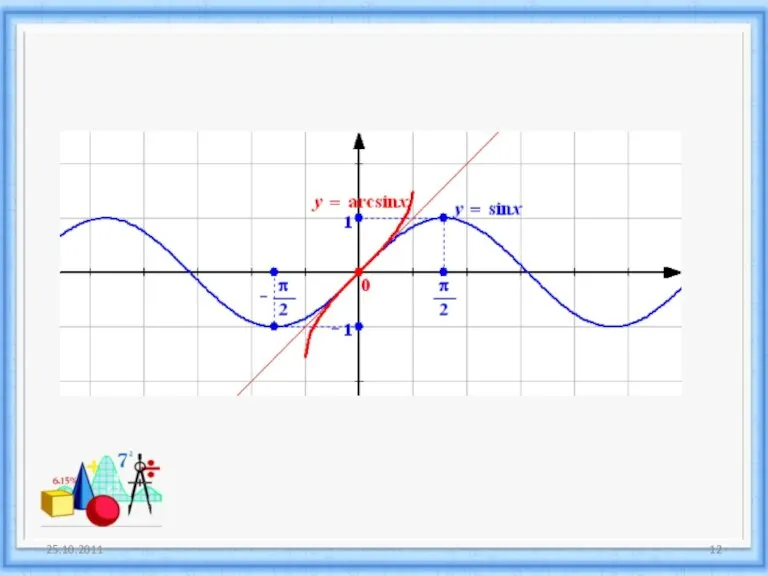
- 11. прямая y=sin x D(y)= E(y)= обратная у= D(y)= E(y)= [-1;1] [-1;1] arcsin x Графики симметричны относительно
- 13. 1. D(х) = [-1;1]. 2. Е(х) = - ; . 3. Функция является нечетной: arcsin (-x)
- 14. IV. Работа в группах Задание: работая по схеме, вместе нами разработанной , дайте определение, перечислите свойства
- 15. V. Инсерт
- 16. VI. Рефлексия Синквейн (пятистишие) Одно существительное Два прилагательных Три глагола Фраза на тему синквейна Существительное синоним
- 17. VII. Подведение итогов VIII. Задание на дом: п.8 выучить определения и свойства, записать в тетради примеры
- 19. Скачать презентацию




![прямая y=sin x D(y)= E(y)= обратная у= D(y)= E(y)= [-1;1] [-1;1] arcsin](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338080/slide-10.jpg)
![1. D(х) = [-1;1]. 2. Е(х) = - ; . 3. Функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338080/slide-12.jpg)




 Специальные методы решения квадратных уравнений
Специальные методы решения квадратных уравнений Исследование математических моделей
Исследование математических моделей Размах и мода ряда чисел
Размах и мода ряда чисел Презентация на тему Этика государственного служащего, правила ношения формы
Презентация на тему Этика государственного служащего, правила ношения формы  Презентация на тему Центральная Азия
Презентация на тему Центральная Азия  Уравнения, содержащие знак модуля
Уравнения, содержащие знак модуля  Исследования по теории показателей А.М. Ляпунова
Исследования по теории показателей А.М. Ляпунова Функция y= ІхІ
Функция y= ІхІ Культурно-исторические рекреационные ресурсы Крыма
Культурно-исторические рекреационные ресурсы Крыма Способы задания функции
Способы задания функции  понятие вероятности (9класс)
понятие вероятности (9класс) Презентация на тему Российская Федерация, субъекты Российской Федерации и муниципальные образования как субъекты предпринимател
Презентация на тему Российская Федерация, субъекты Российской Федерации и муниципальные образования как субъекты предпринимател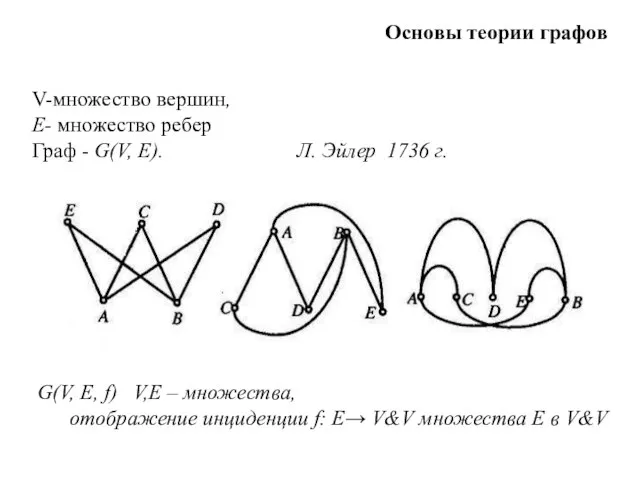 Основы теории графов
Основы теории графов Презентация на тему Особенности древнеегипетского канона
Презентация на тему Особенности древнеегипетского канона Решение показательных уравнений
Решение показательных уравнений Ещё раз о квадратных уравнениях
Ещё раз о квадратных уравнениях mat
mat Формула корней квадратного уравнения
Формула корней квадратного уравнения Квадратный трехчлен 9 класс
Квадратный трехчлен 9 класс Функции y=tg x и y=ctg x, их свойства и графики
Функции y=tg x и y=ctg x, их свойства и графики Формула суммы первых n членов арифметической прогрессии
Формула суммы первых n членов арифметической прогрессии  Презентация на тему Восприятие
Презентация на тему Восприятие  Metod-racionalizacii.pptx
Metod-racionalizacii.pptx Презентация на тему Сущность понятий «подсистемы», «звенья» и «элементы» цепи поставок. Прямые и косвенные каналы (звенья) в цепях
Презентация на тему Сущность понятий «подсистемы», «звенья» и «элементы» цепи поставок. Прямые и косвенные каналы (звенья) в цепях  Квадратичная функция. функция
Квадратичная функция. функция  Полиномы Одночлены Двучлены Трёхчлены Многочлены
Полиномы Одночлены Двучлены Трёхчлены Многочлены  Виды алгоритмов
Виды алгоритмов Тригонометрические неравенства
Тригонометрические неравенства