22.02.2010г. Формулы дифференцирования Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ»
Содержание
- 2. Формулы дифференцирования. Значения функции в данной точке:
- 3. Значения производной функции в этой точке:
- 4. Производная суммы равна сумме производных.
- 5. Лемма: Если функция f дифференцируема в точке х, то она непрерывна в этой точке.
- 6. Постоянный множитель можно выносить за знак производной.
- 9. Решение упражнений № 208б,г № 209а Самостоятельно с последующей проверкой № 209в № 209г
- 12. Скачать презентацию



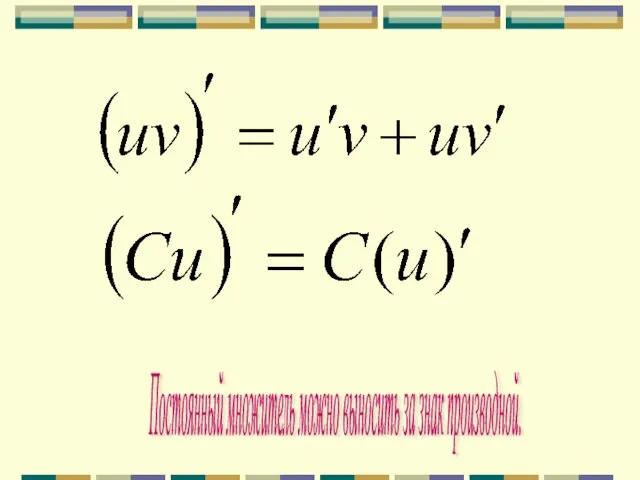

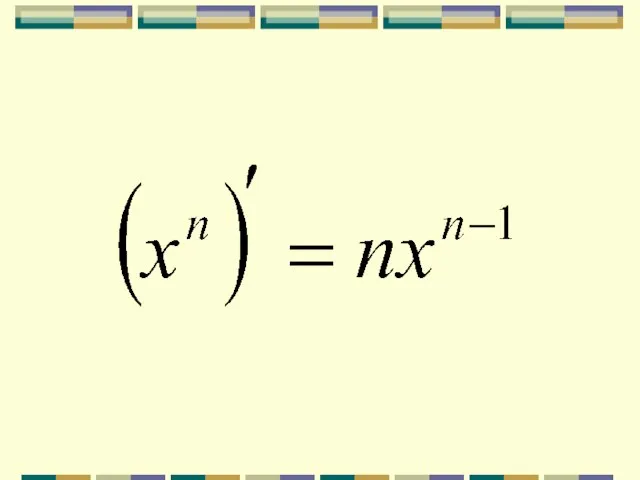


 Презентация на тему Порядок и особенности прохождения государственной службы в таможенных
Презентация на тему Порядок и особенности прохождения государственной службы в таможенных  Линейные уравнения ax=b
Линейные уравнения ax=b Презентация на тему Состояние правового регулирования экологических прав граждан и общественных организаций по российскому зако
Презентация на тему Состояние правового регулирования экологических прав граждан и общественных организаций по российскому зако Презентация на тему Экологическое право: разминка(повторение пройденного материала)
Презентация на тему Экологическое право: разминка(повторение пройденного материала)  Презентация на тему Экзамен без стресса
Презентация на тему Экзамен без стресса  Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к
Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Первообразная
Первообразная Презентация на тему Требования к гос. служащим
Презентация на тему Требования к гос. служащим  Уравнение и его корни 7 класс
Уравнение и его корни 7 класс Презентация на тему Верование Восточных славян
Презентация на тему Верование Восточных славян  Презентация на тему Особенности прохождения гос. службы в правоохранит. органах
Презентация на тему Особенности прохождения гос. службы в правоохранит. органах  Презентация на тему Понятие, предмет, объект, субъект, история развития муниципального права
Презентация на тему Понятие, предмет, объект, субъект, история развития муниципального права  В мире животных. Всё о бобрах
В мире животных. Всё о бобрах Исследование функций и построение графиков
Исследование функций и построение графиков Одночлен и многочлен
Одночлен и многочлен Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Свойства и график функции СИНУС
Свойства и график функции СИНУС Методика обучения решению линейных неравенств с одной переменной
Методика обучения решению линейных неравенств с одной переменной Что такое функция? 7 класс Первый урок по теме «Функции» Составила учитель математики МОУ СОШ №2 Легенчук О.И.
Что такое функция? 7 класс Первый урок по теме «Функции» Составила учитель математики МОУ СОШ №2 Легенчук О.И.  Презентация на тему Рынок недвижимости
Презентация на тему Рынок недвижимости  Франсуа Виет 1540 - 1603
Франсуа Виет 1540 - 1603 Геометрическая прогрессия
Геометрическая прогрессия Математическая логика
Математическая логика Элементы математической статиститки
Элементы математической статиститки  Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена ЭВМ
ЭВМ Статистическое определение вероятности
Статистическое определение вероятности