Понятие бесконечной интегральной суммы. Интеграл

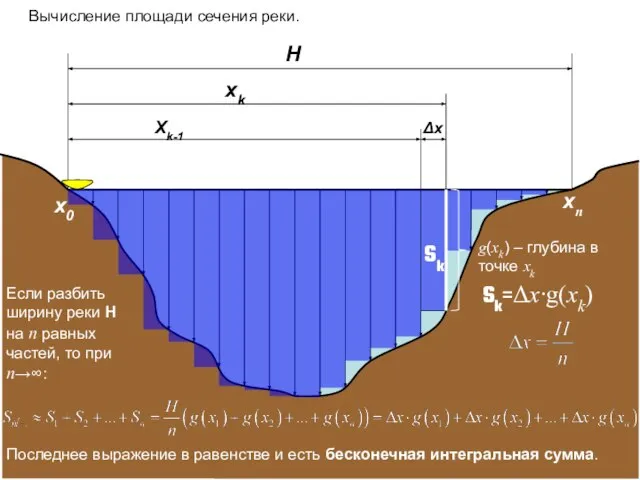
H
xk
Xk-1
Вычисление площади сечения реки.
Δх
Sk
g(xk) – глубина в точке xk
Если разбить ширину реки H на n равных частей, то при n→∞:
Sk=Δx∙g(xk)
x0
xn
Последнее выражение в равенстве и есть бесконечная интегральная сумма.

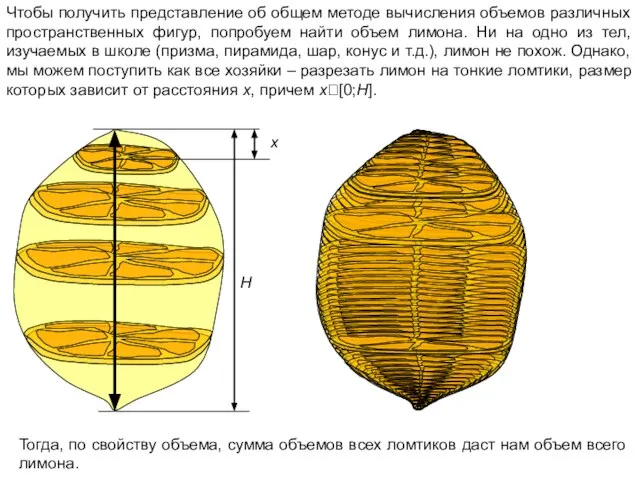
Чтобы получить представление об общем методе вычисления объемов различных пространственных фигур, попробуем найти объем лимона. Ни на одно из тел, изучаемых в школе (призма, пирамида, шар, конус и т.д.), лимон не похож. Однако, мы можем поступить как все хозяйки – разрезать лимон на тонкие ломтики, размер которых зависит от расстояния x, причем x[0;H].
H
x
Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.

H
x
x
С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями, перпендикулярными оси фигуры; причем, если принять число разбиений бесконечно большим числом (n→), то:
Проще говоря, при бесконечном числе разбиений каждый ломтик «вырождается» в плоское сечение и объем лимона равен бесконечной интегральной сумме площадей таких сечений, зависящих от расстояния x, т.е.
где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x[0;H].
Sсеч.
Примечание. ∑ – так сокращенно обозначают знак суммы.

x
H
x[0;H]
0
x
Применяя понятие бесконечной интегральной суммы попробуйте самостоятельно объяснить данный пример и вывод окончательной формулы объёма прямоугольного параллелепипеда (для проверки ☺):
Vпр.пар.=(S1+S2+…+Sn)∙Δx=n∙Sосн.∙ = Sосн.∙H
Объем прямоугольного параллелепипеда равен бесконечной интегральной сумме площадей сечения (равных площади основания) на промежутке [0; H] (взятых вдоль высоты).

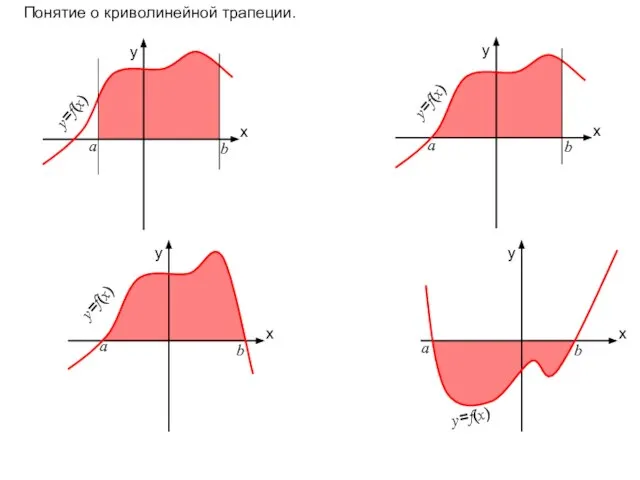
x
y
x
y
x
y
x
y
Понятие о криволинейной трапеции.
а
b
y=f(x)
а
b
а
b
а
b
y=f(x)
y=f(x)
y=f(x)

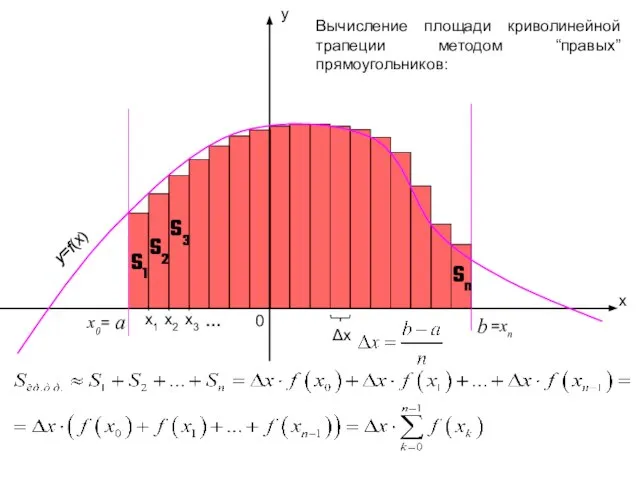
x1
x
y
a
b
0
x2
x0=
x3
=xn
y=f(x)
…
Δx
Вычисление площади криволинейной трапеции методом “правых” прямоугольников:
S1
S2
S3
Sn

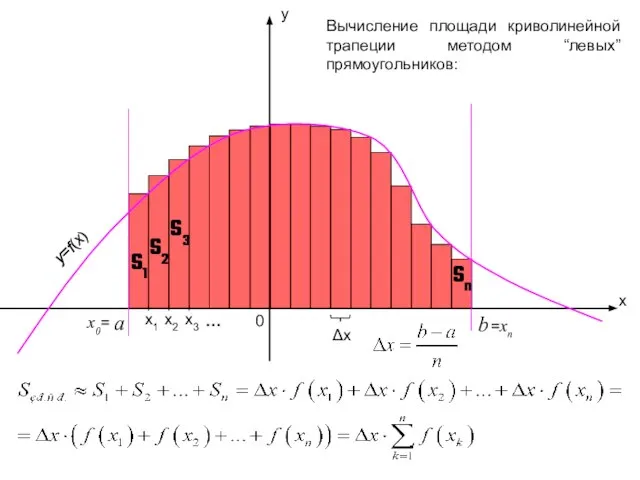
x
y
a
b
0
Δx
Вычисление площади криволинейной трапеции методом “левых” прямоугольников:
x1
x3
x2
y=f(x)
x0=
=xn
…
S1
S2
S3
Sn

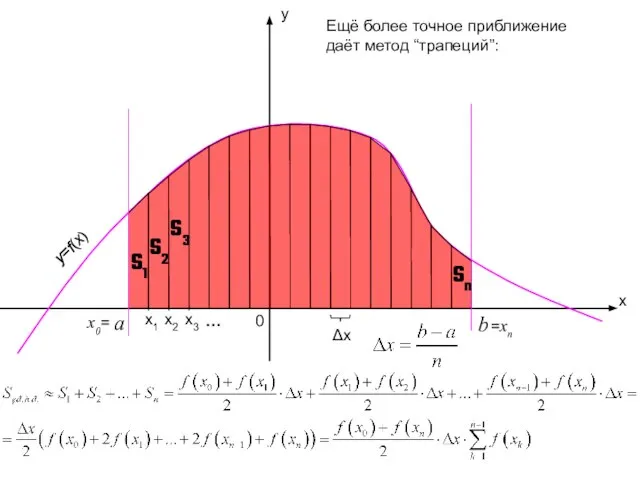
x
y
0
Δx
Ещё более точное приближение даёт метод “трапеций”:
y=f(x)
a
x1
x3
x2
x0=
…
b
=xn
S1
S2
S3
Sn

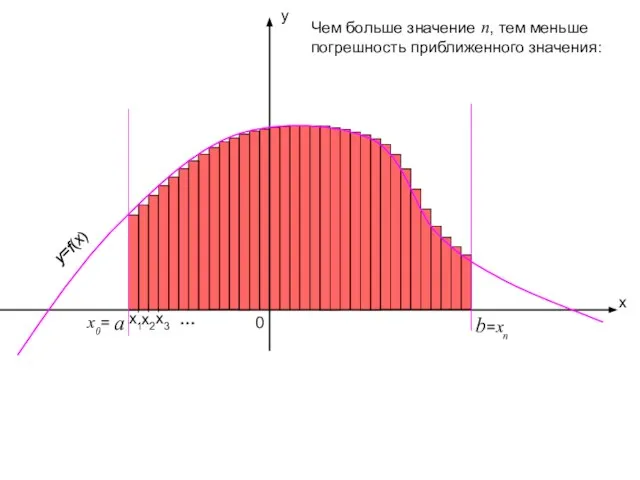
x
y
b
0
x2
x1
x3
=xn
…
Чем больше значение n, тем меньше погрешность приближенного значения:
y=f(x)
a
x0=

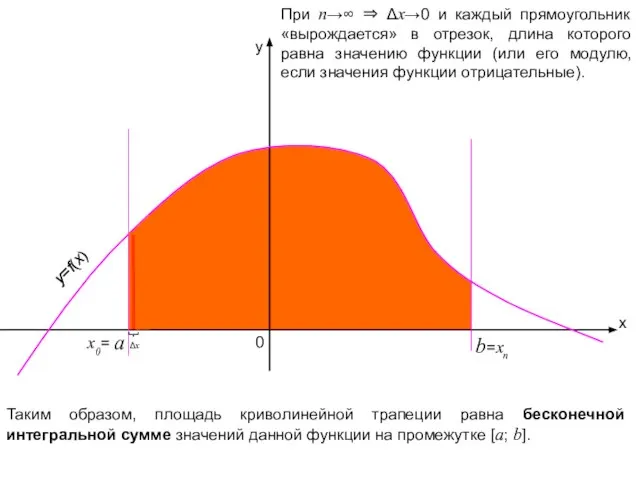
x
y
b
0
=xn
При n→∞ ⇒ Δx→0 и каждый прямоугольник «вырождается» в отрезок, длина которого равна значению функции (или его модулю, если значения функции отрицательные).
y=f(x)
a
x0=
Таким образом, площадь криволинейной трапеции равна бесконечной интегральной сумме значений данной функции на промежутке [a; b].
Δx

В приведенном выше примере мы находили площадь криволинейной трапеции с помощью понятия бесконечной интегральной суммы значений данной функции f(x) на отрезке [a; b]. В математике принята более короткая запись этого понятия – интеграл (∫), т.е.
Примечание. Обратите внимание, что знак интеграла напоминает стилизованную букву S, что естественно из геометрического смысла этого понятия.
Читают: интеграл от a до b эф от икс дэ икс.
Число a называют нижним пределом интегрирования, b – верхним пределом интегрирования, f(x) – подынтегральной функцией, x – переменной интегрирования.
Если Вы владеете понятием предела (lim), то можно дать следующее определение интеграла:
, где xn∈[a; b].

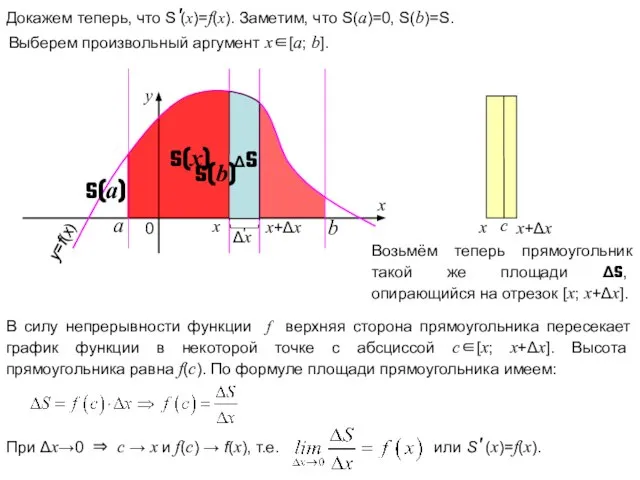
x+Δx
x
y
0
x
y=f(x)
Докажем теперь, что S'(x)=f(x). Заметим, что S(a)=0, S(b)=S.
ΔS
Δx
b
a
x+Δx
x
Возьмём теперь прямоугольник такой же площади ΔS, опирающийся на отрезок [x; x+Δx].
c
В силу непрерывности функции f верхняя сторона прямоугольника пересекает график функции в некоторой точке с абсциссой c∈[x; x+Δx]. Высота прямоугольника равна f(c). По формуле площади прямоугольника имеем:
S(x)
Выберем произвольный аргумент x∈[a; b].
S(a)
S(b)

Важно!!! понимать, что значение интеграла может получиться отрицательным (если, например, на заданном промежутке значения функции отрицательны).
Вы уже знакомы с понятием первообрáзной функции. Доказанное нами утверждение S'(x)=f(x) в силу основного свойства первообразных для всех x∈[a;b] означает, что:
S(x)=F(x)+C,
где С – некоторая постоянная, а F – одна из первообразных для функции f(x).
Для нахождения С подставим x=a:
F(a)+C=S(a)=0
F(a)=–C.
Следовательно, S(x)=F(x) –F(a).
Поскольку площадь криволинейной трапеции равна S(b)=S, подставляя x=b, получим:
S = S(b) = F(b) – F(a)=

Пример 1.
Пример 2.
Отметим некоторые свойства интеграла (объясните их с помощью учителя):
Применение этих свойств часто упрощает вычисление интегралов.
, где c∈[a; b]
, где c∈