Решение неравенств с одной переменной 8 класс

Устная работа
1. Умножьте обе части неравенства на указанное число
и прокомментируйте свои действия:
1) 0,5 < 0,7 на 4
Ответ:
2 < 2,8
1 > 1 на - 12
3 4
Ответ:
-4 < -3
3) 3k< 10 на 2
Ответ:
6k < 20
4) -4d > -7 на -3
Ответ:
12d < 21
правило
правило
правило

Если обе части неравенства умножаются на положительное число, то знак неравенства не меняется

Если обе части неравенства умножаются на отрицательное число, то знак неравенства меняется на противоположный

Произведение двух отрицательных чисел положительно

Верно ли утверждение?
1. Если x > 2 и y > 3, то xy > 6 ?
Ответ:
Утверждение верно
2. Если x < -5 и y < 4 то x + y < 0 ?
Ответ:
Утверждение верно
РЕШЕНИЕ: при сложении неравенств одинакового знака x<-5 и y<4, получается неравенство того же знака x+y< -5+4, или x+y<-1, а значит x+y<0, то есть, утверждение верно
РЕШЕНИЕ: при умножении неравенств одинакового знака x>2 и y>3 , у которых левые и правые части положительны, получается неравенство того же знака xy>6, то есть утверждение верно

Решите неравенство и выберите правильный ответ
1). 5x – 3 > 2.
г). (1; +∞)
РЕШЕНИЕ: 5х -3>2. если перенести из одной части неравенства в другую любое число, переменив при этом его знак, то знак неравенства не меняется .
5х>2+3; 5х>5;
Если обе части неравенства разделить на положительное число, то знак неравенства не меняется x>1.
Так, как неравенство строгое, решением является промежуток (1; +∞)
Верно!
Подумай!
Проверь себя

Решите неравенство и выберите правильный ответ
1). -4 ≤ -2х ≤ 10
а). (-5; 2) б). ⦋-5; 2)
г). (-5; 2⦌
в). ⦋-5; 2⦌
РЕШЕНИЕ: -4 ≤ -2х ≤ 10. если обе части неравенства разделить на отрицательное число -2, то знак неравенства меняется на противоположный.
2 ≥ х ≥ -5 или -5 ≤ х ≤ 2.
Значит, с учетом того, что неравенство нестрогое, решением неравенства является отрезок
⦋-5; 2⦌
ПОМОЩЬ
БУДЬ ВНИМАТЕЛЬНЕЕ!
МОЛОДЦЫ!

Вариант 2
Вариант 1
Выполните задания
1). Докажите, что:
Если (х-2)(х+3)> (х+2)(х-3), то х > 2; Если (х+1)(х+2)>(х+2)(х-3), то х < 0
2). Решите неравенство
7(х+1)+10>11-7(2-х) 5(1-х)-4>7-5х
3). Решите задачу
Сторона прямоугольного пенала больше 5 см, вторая сторона больше первой в 3 раза. Правильно ли, что периметр пенала больше 40 см?
Одна сторона треугольника равна 7 см, другая –10 см. какова наибольшая длина третьей стороны треугольника в целых числах?

Ответы и решения к варианту 1
1). Доказательство:
(х-2)(х+3)>(х+2)(х-3);
х2-2х+3х-6 > х2+2х-3х-6;
х2+х-6 > х2-х-6;
х2- х2+х+х > -6+6;
2х > 0; х > 0
Ответ: х > 0
2). Решение:
7(х+1)+10 > 11-7(2-х);
7х+7+10 > 11- 14 +7х;
7х+17 > -3+7х;
7х-7х > -3-17; 0х > -20
Последнее неравенство 0х > -20 является верным при любом значении х, т.к. его левая часть всегда равна 0
Ответ: любое число
3). Решение:
Принимаем одну из сторон пенала за х. по условию задачи она должна быть больше 5 см, получаем неравенство х > 5. Другая сторона пенала больше первой в 3 раза, т.е. 3х > 15. периметр прямоугольного пенала равен 2(х+3х) > 2(5+15), при упрощении данного неравенства получаем 8х > 40, следовательно предположение, выдвинутое в задании верно.
Ответ: предположение верно
3х
х

1).Доказательство:
(х+1)(х-6) > (х+7)(х-3);
х2+х-6х-6 > х2+2х-3х-6;
х2-5х-6 > х2-х-6;
х2- х2+х-5х > -6+6;
-4х > 0; х < 0.
Ответ: х < 0
Ответы и решения к варианту 2
2). Решение:
5(1-х)-4 > 7-5х;
5-5х-4 > 7-5х;
-5х +1 > 7-5х;
-5х+5х>7-1; 0х > 6.
Данное неравенство не имеет решений т.к. последнее неравенство 0х > 6 неверно.
Ответ: решений нет
3).Решение . Сумма двух сторон треугольника должна быть больше третьей стороны. В данном случае третья сторона треугольника не должна быть длиннее суммы двух других его сторон. Обозначим длину неизвестной стороны за х. получим неравенство: х < 10+7 или х < 17. т.к. неравенство строгое число 17 не является решением неравенства. Значит наибольшая длина третьей стороны треугольника – 16 см
Ответ: 16 сантиметров
10см
7см
?

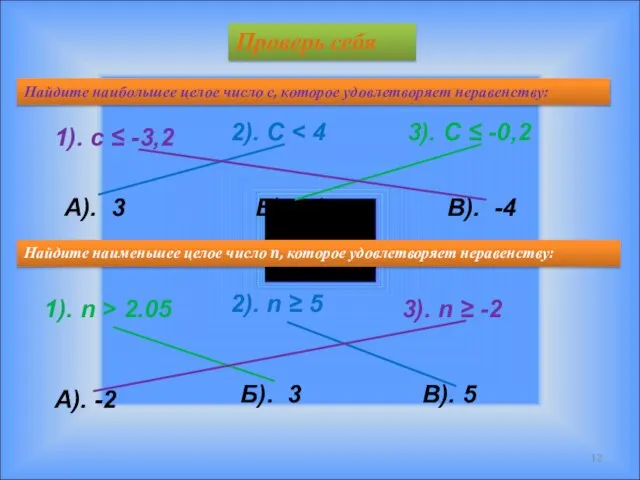
Проверь себя
1). с ≤ -3,2
2). С < 4
3). С ≤ -0,2
Найдите наибольшее целое число с, которое удовлетворяет неравенству:
А). 3
В). -4
Б). -1
Найдите наименьшее целое число n, которое удовлетворяет неравенству:
1). n > 2.05
2). n ≥ 5
3). n ≥ -2
А). -2
Б). 3
В). 5

Самостоятельная работа
1. При каких значениях z выражение принимает отрицательное значение:
2)
2. При каких значениях у сумма дробей и
меньше значения дроби
3. При каких значениях a разность дробей и
меньше или равна