Синус и косинус угла «Алгебраическое» определение

1-й блок
слайдов
Харьковский В.З.

Что такое косинус угла ?
Это число, которое можно определить следующим образом:
Харьковский В.З.

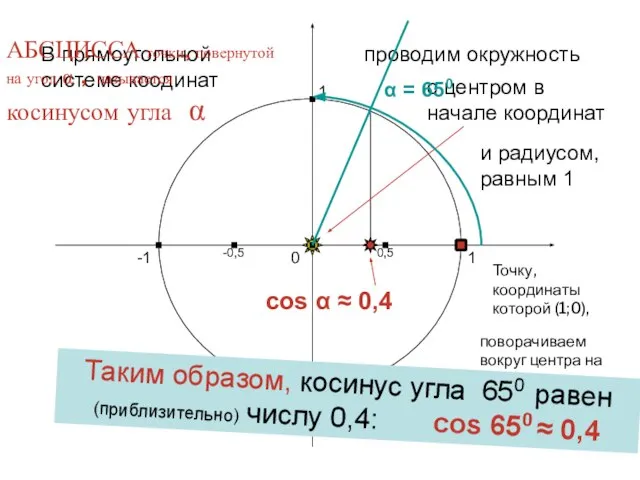
cos α ≈ 0,4
1
0
-1
1
-1
В прямоугольной системе коодинат
проводим окружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
АБСЦИССА точки, повернутой на угол α , называется косинусом угла α
α = 650
0,5
-0,5
Таким образом, косинус угла 650 равен (приблизительно) числу 0,4: cos 650 ≈ 0,4
Харьковский В.З.

ЗАПОМНИМ:
поворот точки на положительный угол выполняется против часовой стрелки
поворот точки на отрицательный угол выполняется по часовой стрелке
Харьковский В.З.

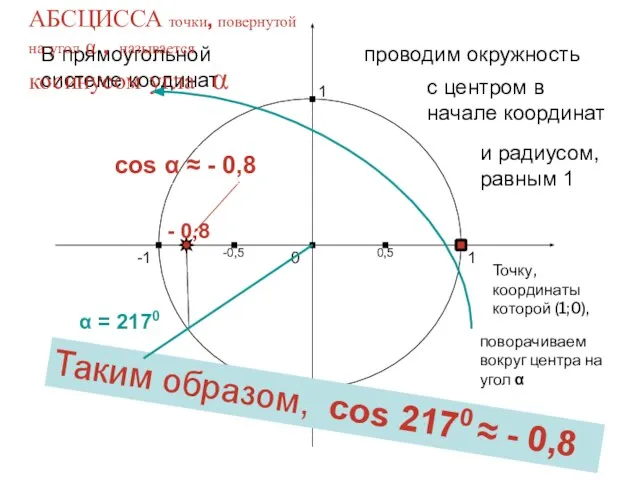
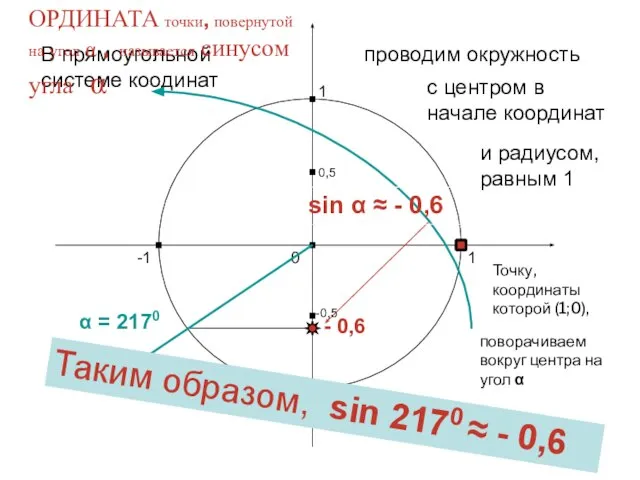
Найдем теперь косинус другого угла,
например – угла 217 0
Харьковский В.З.

1
0
-1
1
-1
В прямоугольной системе коодинат
проводим окружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
АБСЦИССА точки, повернутой на угол α , называется косинусом угла α
α = 2170
0,5
-0,5
Таким образом, cos 2170 ≈ - 0,8
- 0,8
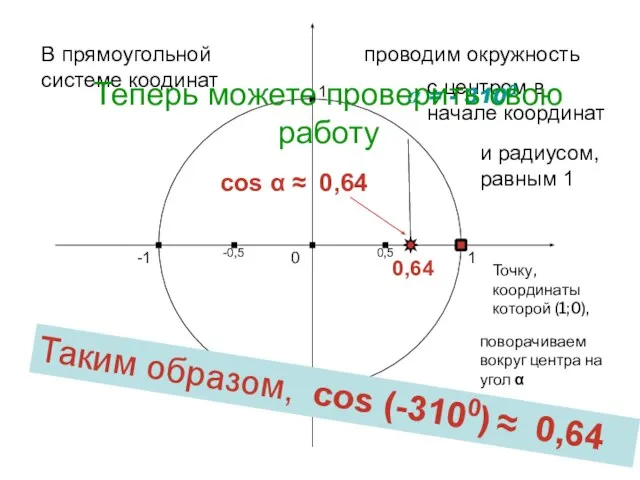
cos α ≈ - 0,8

Попробуйте теперь сами:
выполните чертеж и определите (приближенно) косинус угла -3100
Харьковский В.З.

Помните: поворот точки на отрицательный угол выполняется по часовой стрелке
Харьковский В.З.

Итак, вам следует:
в прямоугольной системе координат построить окружность (центр – начало координат, радиус – единичный отрезок);
отметить точку (1;0);
повернуть ее (вокруг начала координат) на угол -3100;
определить абсциссу получившейся точки – это и есть косинус угла -3100;
записать результат: cos (-3100) ≈ …
только после выполнения этого задания можете продолжить просмотр
Харьковский В.З.

cos α ≈ 0,64
1
0
-1
1
-1
В прямоугольной системе коодинат
проводим окружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
α = - 3100
0,5
-0,5
Таким образом, cos (-3100) ≈ 0,64
0,64
Теперь можете проверить свою работу
Харьковский В.З.

2-й блок
слайдов
Харьковский В.З.

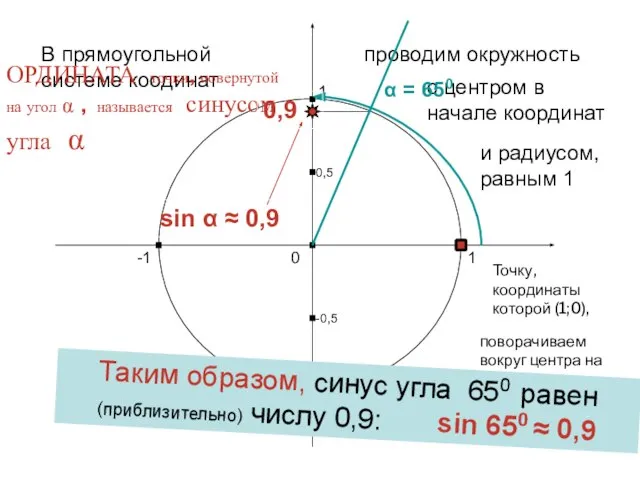
Что такое синус угла ?
Это число, которое можно определить следующим образом:
Харьковский В.З.

1
0
-1
1
-1
В прямоугольной системе коодинат
проводим окружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
ОРДИНАТА точки, повернутой на угол α , называется синусом угла α
α = 650
0,5
-0,5
Таким образом, синус угла 650 равен (приблизительно) числу 0,9: sin 650 ≈ 0,9
sin α ≈ 0,9
0,9
Харьковский В.З.

Найдем теперь синус другого угла,
например – угла 217 0
Харьковский В.З.

1
0
-1
1
-1
В прямоугольной системе коодинат
проводим окружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
ОРДИНАТА точки, повернутой на угол α , называется синусом угла α
α = 2170
0,5
-0,5
- 0,6
sin α ≈ - 0,6
Таким образом, sin 2170 ≈ - 0,6

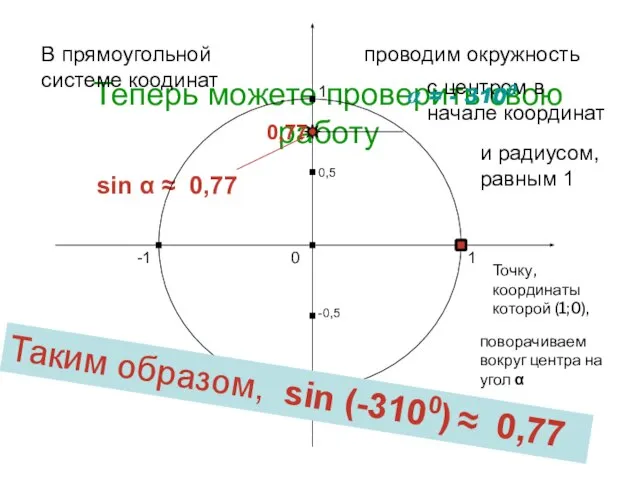
Снова попробуйте сами:
с помощью имеющегося у Вас чертежа определите (приближенно) синус угла -3100

Помните:
синус угла – это ордината точки
Харьковский В.З.

Теперь можете проверить свою работу
sin α ≈ 0,77
1
0
-1
1
-1
В прямоугольной системе коодинат
проводим окружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
α = - 3100
0,5
-0,5
0,77
Таким образом, sin (-3100) ≈ 0,77
Харьковский В.З.

3-й блок
слайдов
Харьковский В.З.

А теперь задания:
Вычислите:
cos 900
sin (-900)
sin 2700
cos (-1800)
cos 3600
sin (-18000)
cos 9000
sin (-4500)
Сравните
cos 230 и cos 380
sin 3000 и sin 3030
cos (-1180) и cos (-1280)
sin 10 и cos (-2690)
sin (-6000 ) и cos (-6000)
Харьковский В.З.

1
0
-1
1
-1
Харьковский В.З.

А это – для «продвинутых»:
Сравните:
sin 1230 и sin 560
Вычислите:
sin 1600 · cos (-2000) · cos 8100 · sin 10000
Харьковский В.З.

1
0
-1
1
-1
Харьковский В.З.